NO:01

“ 现在已然衰朽者,将来可能重放异彩。现在备受青睐者,将来却可能黯然失色。” 当事物发展严重偏离其均值时,均值会像万有引力一样令其回归。如果时间足够长,万物都终将回归于其均值。正所谓:盛极必衰,否极泰来。
在金融学中,均值回归是价格偏离均价或价值一定程度后向其靠拢的规律。本质上,均值回归就是哲学思想中所说的『物极必反』。用大白话可以简单地概括为 “ 涨多必跌,跌多必涨 ” 。
NO:02
在商品期货交易中,对于均值回归模型的应用场景,选择跨期价差是非常理想的交易标的。即对不同交割期的合约同时进入低买高卖,当合约间价差过高或过低时,相应的卖出或买入价差,等价差回归均衡价差后,再平仓从而获利。

如上图所示:均值回归模型的基础是跨期价差的回归和震荡特征。理论上,在期货定价和期现套利的作用下,跨期合约间存在稳定的、可量化的价差关系。
当两个合约的价差偏离均衡价差一定程度后,会有向均衡价差回复的走势,那么,我们可以据此构造均值回归模型。
NO:03
FG1809合约 - FG1805合约 价差走势图

MA1809合约 - MA1805合约 价差走势图

如上图所示,价差通常会以其均值为中心上下波动。也就是说,当价差由于波动而偏离均值时,它将调整并重新归于均值。那么如果我们如果能捕捉偏离价差的回归,就可以从此获利。值得注意的是:合约到期月份相差越多,跨期价差波动空间越大。
但如果考虑到资金的时间成本,等待价差回归,也是很不划算的。那么就需要对价差均值进行重新定义,以简单均线或自适应均线来代替均值,找到短周期的一种获利方法。
NO:04
在这之前,就需要引入标准差(standard deviation)的概念,通常用小写希腊字母。σ(sigma,读 “ 西格玛 ”)。
通俗地讲,一组数据的标准差就是这组数据离均值的普遍差距。标准差的计算公式为:
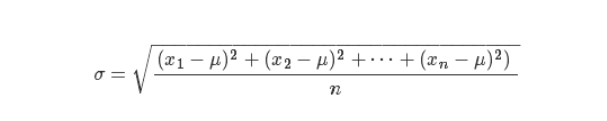
如果这组数据的波动较大,那么 σ 相应也会较大;相反的,如果这组数据波动小,那么 σ 会更接近零。
具体的,用滞后一段时间的价差均线作为均衡价差,以均线加上若干倍的标准差作为开仓标准和止损标准,当价差偏离超过若干个标准差后策略开仓,而偏离更多时则止损。
NO:05
此外,由于真实套利过程中,不管是人工下单还是量化交易,套利交易无法对价差瞬时的噪声性的偏离即时反应,所以只能捕捉一定市场内持续的偏离。

根据如上模型原理,在判断套利开平仓条件时,把移动均值 μ 均衡价差,k 为止损系数,μ + a * σ 与 μ - a * σ 为套利上下界构造跨期套利策略:
1、当 μ1 > μ + a * σ 时,价差突破套利区间上限,此时认为价差偏大,则以最近 1 分钟价格做空价差,即熊市套利策略。
2、当 μ1 > μ + a * σ * k 时,价差突破套利区间上限至更多,此时认为价差可能会更大,则止损,熊市套利策略结束。
3、当 μ1 < μ - b * σ 时,价差突破套利区间下限,此时认为价差偏小,则以最近 1 分钟价格做多价差,即牛市套利策略。
4、当 μ1 < μ - b * σ * k 时,价差突破套利区间下限至更多,此时认为价差可能会更小,则止损,牛市套利策略结束。
NO:06
需要提醒的是,在不同市场环境下跨期套利价差的分布特点不同,使用的跨期套利上下阈值也不同,a 与 b 越大,价差波动区间越大,开仓条件越苛刻,套利次数减小,但是单次套利的获利空间增加。
价差成交次数分布图

反之 a 与 b 越小,虽然增加了套利实施的次数,但交易成本也随之增加,单次套利收益空间缩小。
NO:07
接下来,我们利用 量化交易平台进一步操作,来实现一个均值回归模型的实例,从而验证我的们理论,是否能发现赚钱的机会。
数据准备:
我们直接使用数据库数据,代码如下:

第一行:调用 K 线数组;
第二行:过滤 K 线数组长度;
第六行:调用 talib 库 BOLL 指标;
第七行:定义套利区间上限;
第八行:定义均值;
第九行:定义套利区间下限;
十行以下:计算实时价差,及其他方便后续的数据处理。
策略逻辑代码:

NO:08
利用交易信号数据,进行模拟测试。我们设定交易参数和规则:
本金:1 万
合约:MA
K 线周期:1 分钟
时间跨度:3 个月
手续费为 5 元
数据类型:模拟级 Tick
绩效如下:

NO:09
基于上述的均值回归模型,我们还可以分别从开平仓方式两个角度,通过均值斜率条件,来动态的调整套利上限、下限阈值。

如上图,以熊市套利为例,我们通过计算下降中的均值斜率:
z = ( y2 - y1 ) / ( x2 - x1 )
调整后的套利上限、下限:
μ + a * σ * ( z + 1 )
μ - a * σ * ( z + 1 )
相比之前的模型的开平仓方式,调整后的策略模型,可以在套利上、下阈值上更具有灵活性。

在不同的市场条件下,通过均值斜率动态的调整套利上限、下限阈值,可以是模型更加适应当前的市场状态。降低因价差大幅波动,造成的止损。并且单次增加跨期套利的获利空间。
关于均值回归模型的改进只是理论上的设想,哪个小伙伴感兴趣,可以直接在本公众号内回复 “ 均值回归 ” ,直接领取原版源码并加以改进。
来源:宽客在线
--------------------------------------------
拓展阅读:
来源:CSDN
作者:小壁虎的春天
链接:https://blog.csdn.net/zk168_net/article/details/103615768