这道题用康托展开的思想进行求解。
康托展开运算
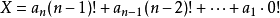
其中, 为整数,并且 。
表示原数的第i位在当前未出现的元素中是排在第几个
z康托展开的逆运算
既然康托展开是一个双射,那么一定可以通过康托展开值求出原排列,即可以求出n的全排列中第x大排列。
逆康托展开举例
一开始已经提过了,康托展开是一个全排列到一个自然数的双射,因此是可逆的。给出数组(1,2,3,4,5)与位次62,具体过程如下:
由于要算比当前数小的数,所以要将62-1=61
用 61 / 4! = 2余13,说明,说明比首位小的数有2个,所以首位为3。
用 13 / 3! = 2余1,说明,说明在第二位之后小于第二位的数有2个,所以第二位为4。
用 1 / 2! = 0余1,说明,说明在第三位之后没有小于第三位的数,所以第三位为1。
用 1 / 1! = 1余0,说明,说明在第四位之后小于第四位的数有1个,所以第四位为5。
最后一位自然就是剩下的数2。
通过以上分析,所求排列组合为 34152。
(需要注意的是,逆康托展开算出的比当前位小的数的个数,均针对不包含已选过数字的数组)
代码
class Solution:
def getPermutation(self, n: int, k: int) -> str:
# 计算阶乘
fra = 1
frac = [1]
for i in range(1, n):
fra *= i
frac.append(fra)
# 计算数字
nums = [i for i in range(1, n+1)] # 存储没有被选过的数字
result = []
k -= 1
for i in range(n-1, -1, -1):
tmp = k//frac[i]
k = k%frac[i]
result.append(str(nums[tmp]))
nums.remove(nums[tmp]) # 将已经选过的数字从nums中删除
return "".join(result) # 要将数字列表转化为字符串
终于放假了哈哈哈哈哈哈,考完试了哈哈哈哈哈哈哈哈哈。我又解放了哈哈哈哈哈哈哈哈哈。
来源:CSDN
作者:Emma1997
链接:https://blog.csdn.net/Ema1997/article/details/104075975