分类问题
在分类问题中,你要预测的变量 𝑦 是离散的值,我们将学习一种叫做逻辑回归 (Logistic
Regression) 的算法,这是目前最流行使用最广泛的一种学习算法。
在分类问题中,我们尝试预测的是结果是否属于某一个类(例如正确或错误)。分类问题的例子有:判断一封电子邮件是否是垃圾邮件;判断一次金融交易是否是欺诈;判断肿瘤是恶性还是良性
先从二元分类来讨论
我们将因变量可能属于的两个类别称为正类和负类,我们用0表示负类,用1表示正类。
如果我们用线性回归来解决一个分类问题,线性函数的输出值可能远大于1或者远小于0,那怎么办呢?
所以我们就要逻辑回归的算法的输出值永远在0到1中间
根据线性回归模型,我们只能预测连续值,而逻辑回归预测的是离散值,我们可以假设
当ℎ𝜃(𝑥) >= 0.5时,预测 𝑦 = 1。
当ℎ𝜃(𝑥) < 0.5时,预测 𝑦 = 0 。
我们引入一个新的模型,逻辑回归,该模型的输出变量范围始终在 0 和 1 之间。 逻辑回归模型的假设是: ℎ𝜃(𝑥) = 𝑔(𝜃𝑇𝑋) 其中: 𝑋 代表特征向量 𝑔 代表逻辑函数,是一个常用的逻辑函数为 S 形函数(Sigmoid function)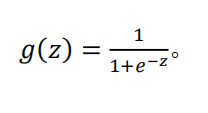
python代码实现
import numpy as np
def sigmoid(z):
return 1 / (1 + np.exp(-z))
函数图像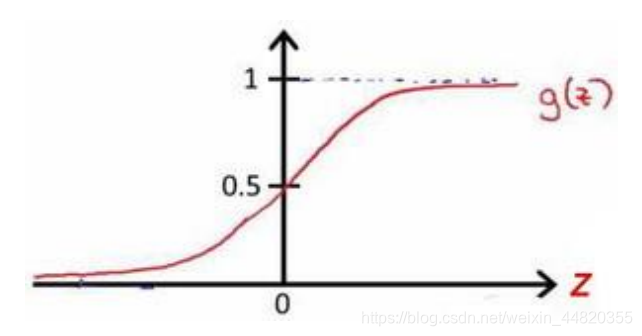
判定边界
现在讲一下决策边界的概念。这个概念能更好的帮助我们理解逻辑回归的假设函数在计算什么。

在逻辑回归中,我们预测:
当ℎ𝜃(𝑥) >= 0.5时,预测 𝑦 = 1。
当ℎ𝜃(𝑥) < 0.5时,预测 𝑦 = 0 。
根据上面绘制出的 S 形函数图像,我们知道当
𝑧 = 0 时 𝑔(𝑧) = 0.5
𝑧 > 0 时 𝑔(𝑧) > 0.5
𝑧 < 0 时 𝑔(𝑧) < 0.5
又 𝑧 = 𝜃𝑇𝑥 ,
即:
𝜃𝑇𝑥 >= 0 时,预测 𝑦 = 1
𝜃𝑇𝑥 < 0 时,预测 𝑦 = 0
现在假设有个模型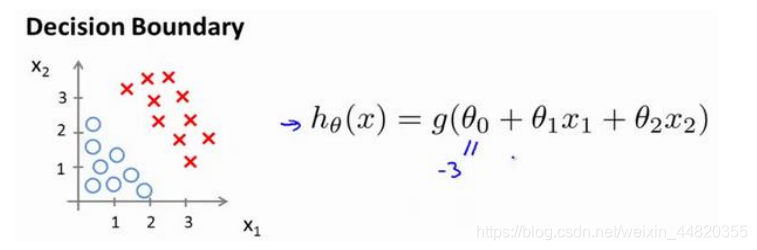
并且参数𝜃 是向量[-3 1 1]。 则当−3 + 𝑥1 + 𝑥2 ≥ 0,即𝑥1 + 𝑥2 ≥ 3时,模型将预测 𝑦 = 1。 我们可以绘制直线𝑥1 + 𝑥2 = 3,这条线便是我们模型的分界线,将预测为 1 的区域和预测为 0 的区域分隔开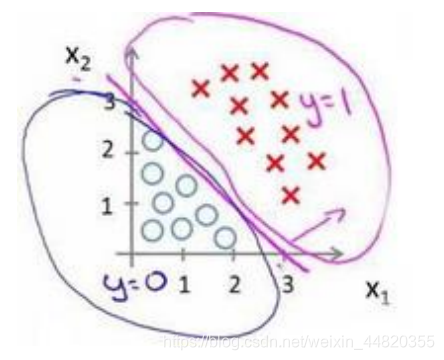
总的来说,决策边界就是找一条直线或者曲线,来划分要区分的类别的区域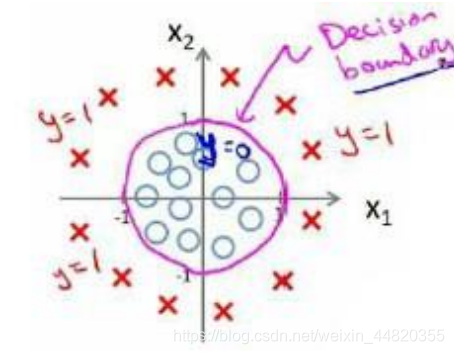
这个模型就需要二次方特征来得到判定边界是一个圆
我们可以用很复杂的模型来适应非常复杂形状的决策边界。
代价函数
在线性回归中,我们定义的代价函数是所有模型误差的平方和。理论上讲,在逻辑回归也可以用这个定义,但是我们将Sigmoid函数带到这个代价函数中,得到的是一个非凸函数。
这意味着此代价函数有很多局部最小值,这会影响梯度下降法找到全局最小值。
我们重新定义逻辑回归的代价函数为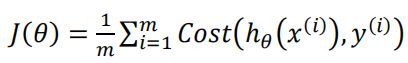
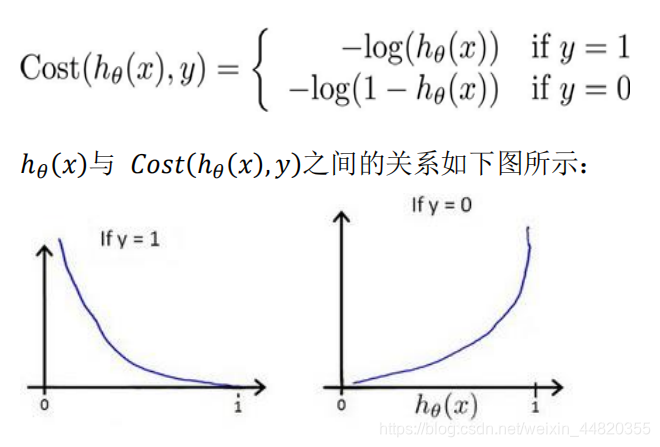
这样构建的𝐶𝑜𝑠𝑡(ℎ𝜃(𝑥), 𝑦)函数的特点是:
当实际的 𝑦 = 1 且ℎ𝜃(𝑥)也为 1 时误差为 0,
当 𝑦 = 1 但ℎ𝜃(𝑥)不为 1 时误差随着ℎ𝜃(𝑥)变小而变大;
当实际的 𝑦 = 0 且ℎ𝜃(𝑥)也为 0 时代价为 0,
当𝑦 = 0 但ℎ𝜃(𝑥)不为 0 时误差随着 ℎ𝜃(𝑥)的变大而变大。
将构建的 𝐶𝑜𝑠𝑡(ℎ𝜃(𝑥), 𝑦)简化如下: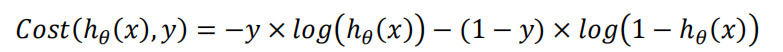
代入到代价函数得: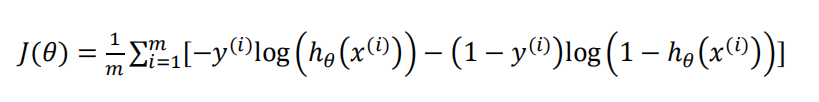
python代码:
import numpy as np
def cost(theta, X, y):
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
first = np.multiply(-y, np.log(sigmoid(X* theta.T)))
second = np.multiply((1 - y), np.log(1 - sigmoid(X* theta.T)))
return np.sum(first - second) / (len(X))
在得到这样一个代价函数以后,我们便可以用梯度下降算法来求得能使代价函数最小的参数了。算法为: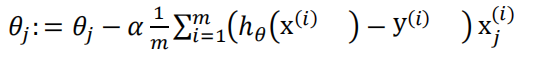
注意:虽然此梯度下降法表面上看上去和线性回归的梯度下降一样,但实际是不一样的。另外,在运行梯度下降算法之前,进行特征缩放是非常必要的
关于此逻辑回归的代价函数会是一个凸优化的问题,代价函数 会是一个凸函数,没有局部最优解
推导过程: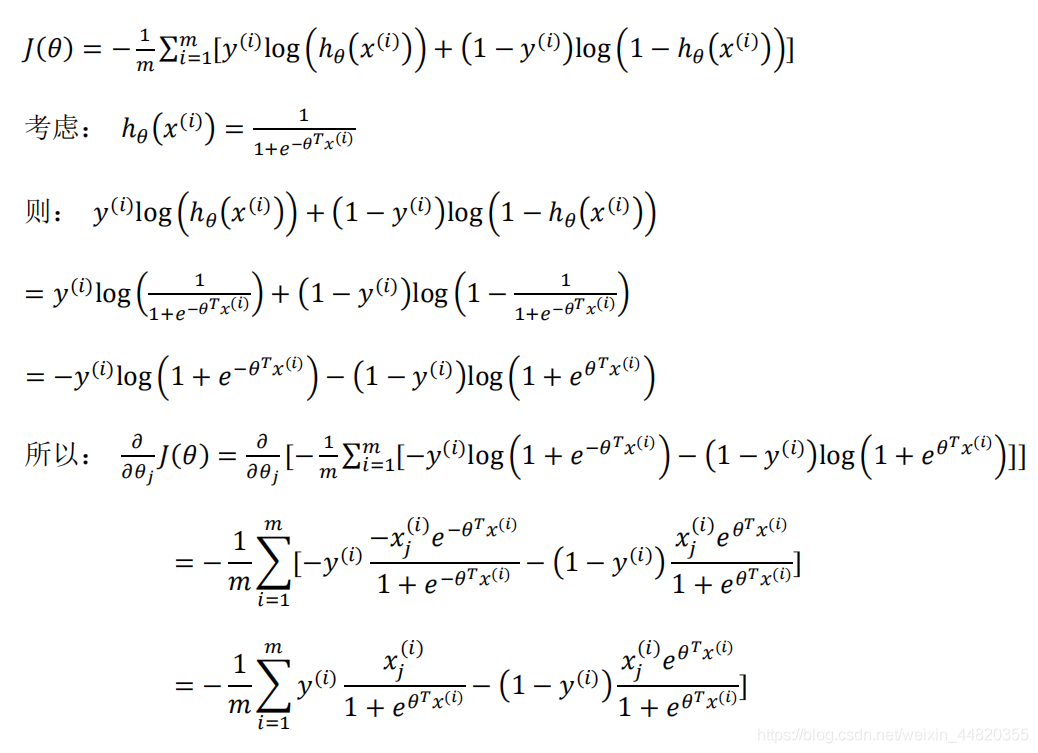
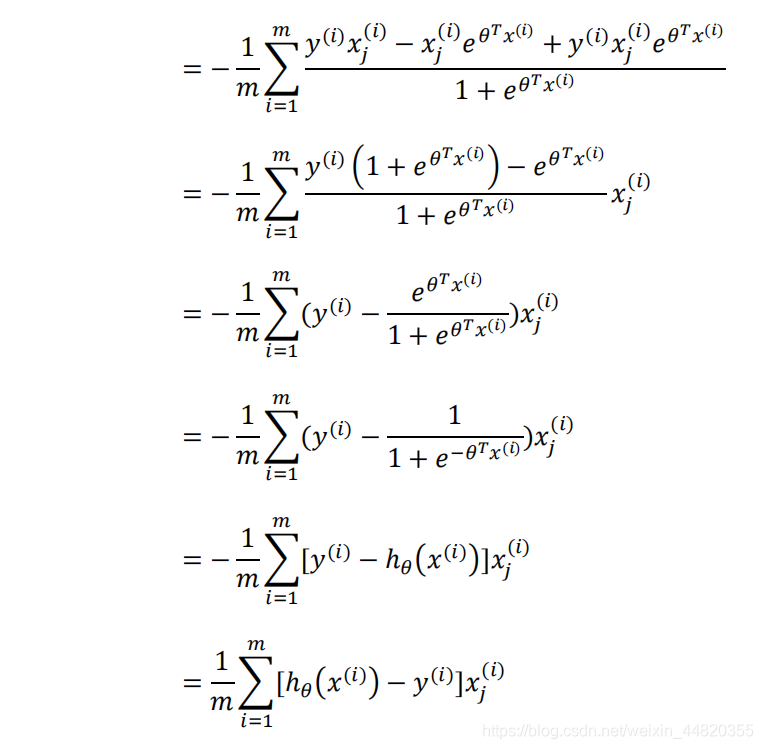
来源:CSDN
作者:吓得我泰勒都展开了
链接:https://blog.csdn.net/weixin_44820355/article/details/104017130