一、问题描述:
旅行商问题:设有n个城市和距离矩阵D=[dij],其中dij表示 城市i到城市j的距离,i,j=1,2 … n,则问题是要找出遍访每个城市恰好一次的一条回路并使其路径长度为最短。
二、实验目的:
在同一组数据中,观察种群数量和参数不一样的情况对实验结果的总结。
三、程序流程
1、根据输入的城市初始化基因序列;
2、计算每个基因序列的适应性,适应性与路径长度成反比(这里我使用路径长度的倒数表示个体适应性);
3、根据个体适应性选择生存下来的个体,也就是根据阈值选择留下来的个体;
4、选择后,个体数小于种群初始个体数,使用轮盘选择方式选择父本;
5、若是选中的父本既定概率大于交叉概率,则直接保留下来,否则通过交叉产生后代
6、后代进行基因突变操作,也就是交换两个节点值;
7、判断是否达到迭代次数,是,结束,返回最优解;否,转到第2步。
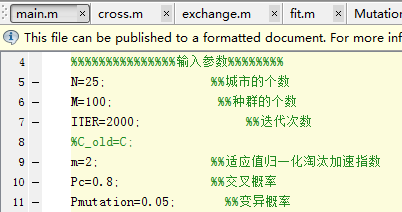
初始参数数据:
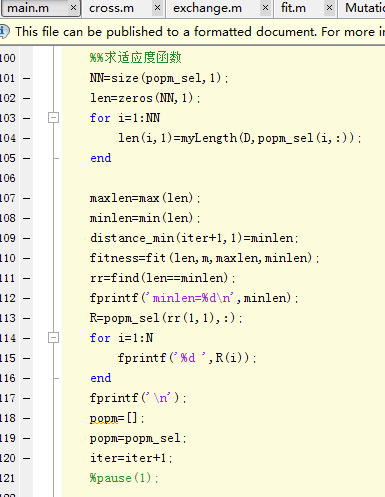
适应度函数:
选择:

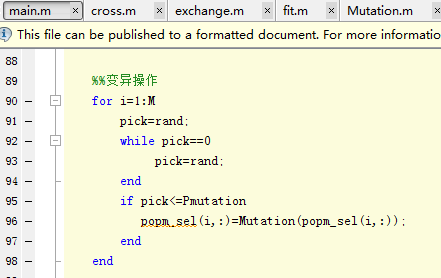
变异:
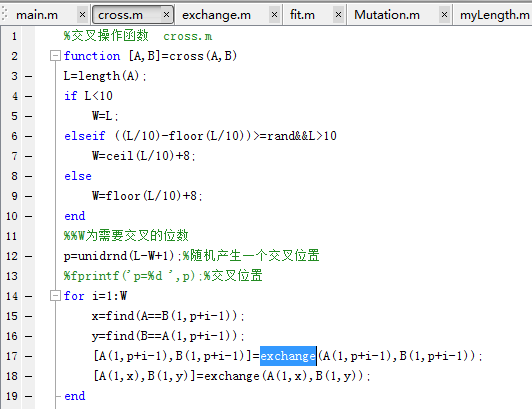
交叉:
初始运行:
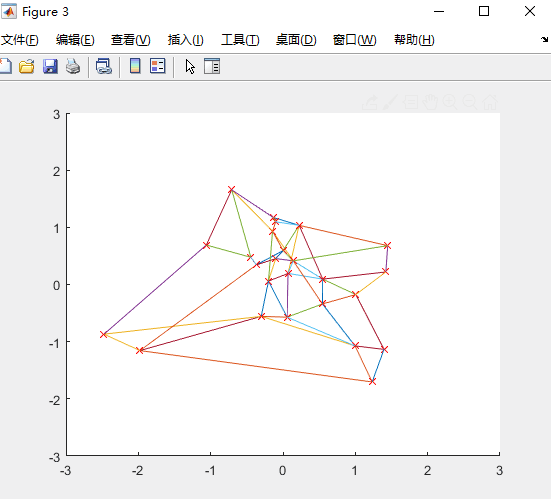
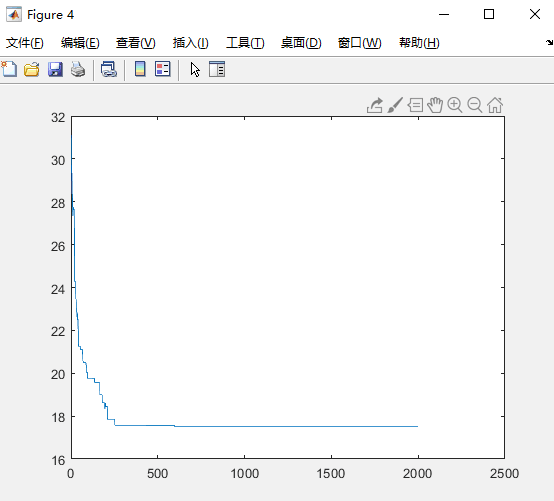
四、实验结论:
主要参数:种群规模、城市数量、最大运行代数、交叉概率、变异概率
1、种群规模对结果的影响
不变参数
变参:种群数量
种群数量M=50:
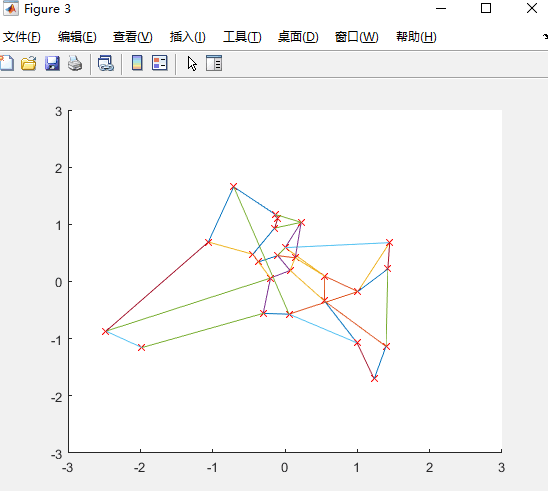
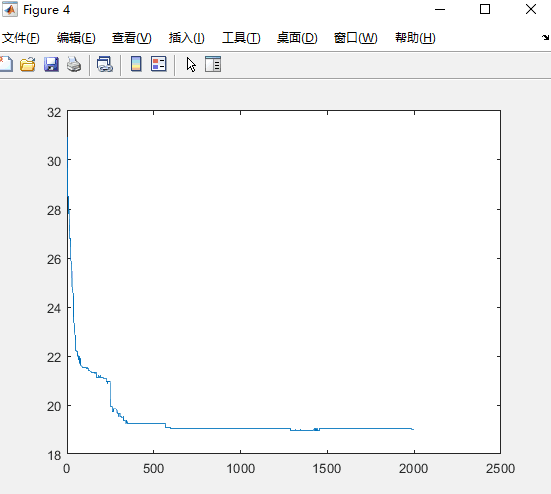
种群数量M=200:
结论:上述情况下,当种群规模大于等于30的时候算法基本能得到正确解,达到40算法能100%得到最短路径,但是最佳路径出现代数并不稳定,种群数量越小收敛越快。
2、最大运行代数对结果的影响
不变参数
变参:最大运行代数
结论:上述情况下,当最大运行代数达到1000时算法运行结果趋于稳定(稳定得到最短路径),这时算法的效率比较高。
当达到10000时100%正确,但是最佳路径出现代数稳定在2000代以内,所以想要2000代之后的计算都是不必要的,算法的最大运行代数最优参数为2000。
3、城市数量对结果的影响
不变参数
变参:城市数量
城市数量N=10:
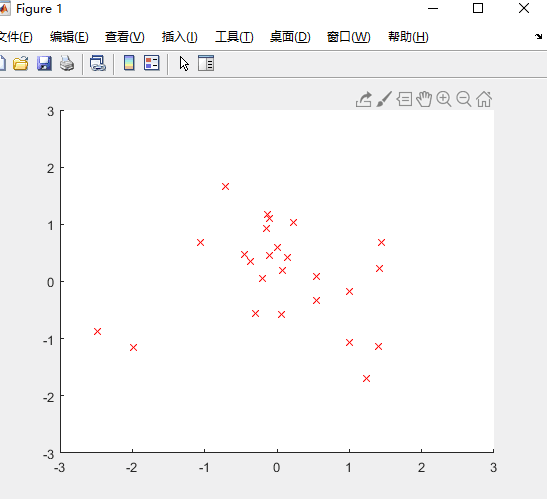
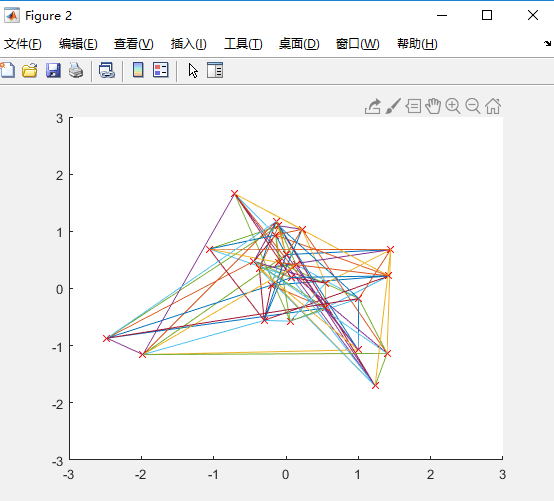
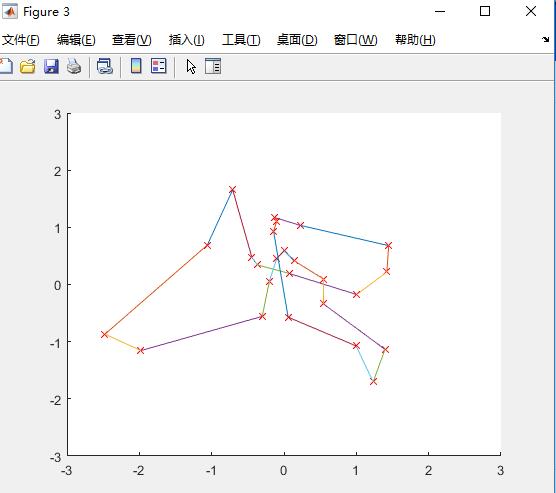
城市数量N=50:
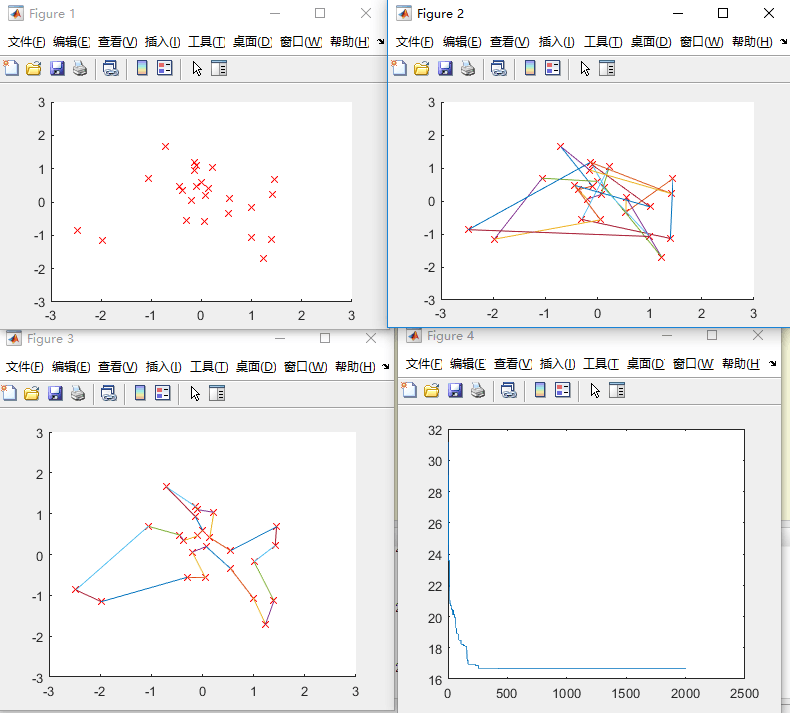
结论:上述情况下,当城市数量<=20时,算法100%的到正确解。当城市数量越大,越难得到最优解。
调整分以下情况:
(2)其他参数不变,最大运行代数逐渐调到10000时,算法结果稳定。
(3)其他参数不变,交叉概率不管怎么调,算法都得不到最优解。但是将种群规模调大到40,交叉概率调为0.1时,算法结果趋于稳定
综合(1)(2)(3)发现似乎一开始交叉概率就有问题,对于该算法交叉概率应该调低。当交叉概率较高时无论是提高种群规模还是最大运行代数,代价都太大。