动态规划之背包问题

动态规划之背包问题

• 01背包问题
• 问题1 为什么01背包问题可以用一维数组来优化？
• 问题2 使用一维数组优化过程中为什么物体的重量要从大到小枚举？
• code1
• code2
• code3
• code（一维数组优化）

01背包问题

问题1 为什么01背包问题可以用一维数组来优化？

用二维数组枚举如下：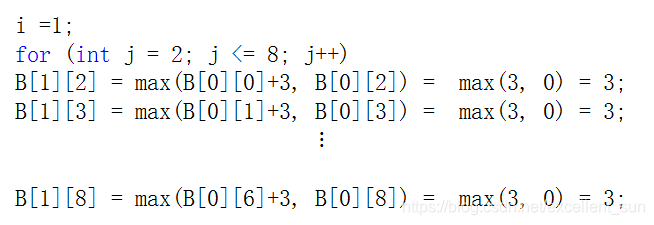




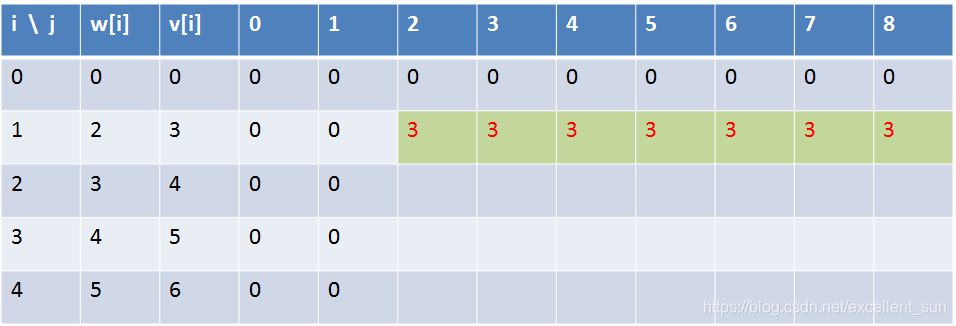
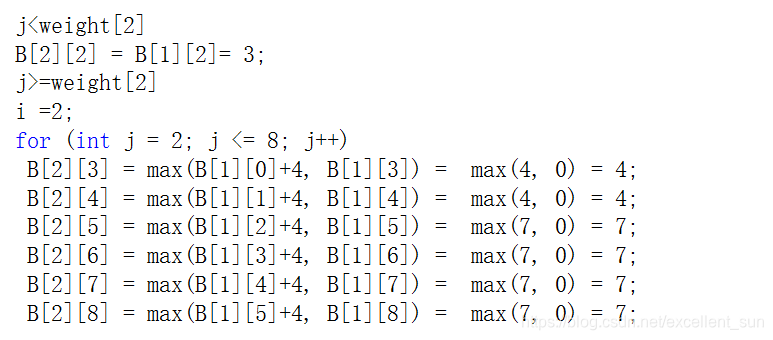
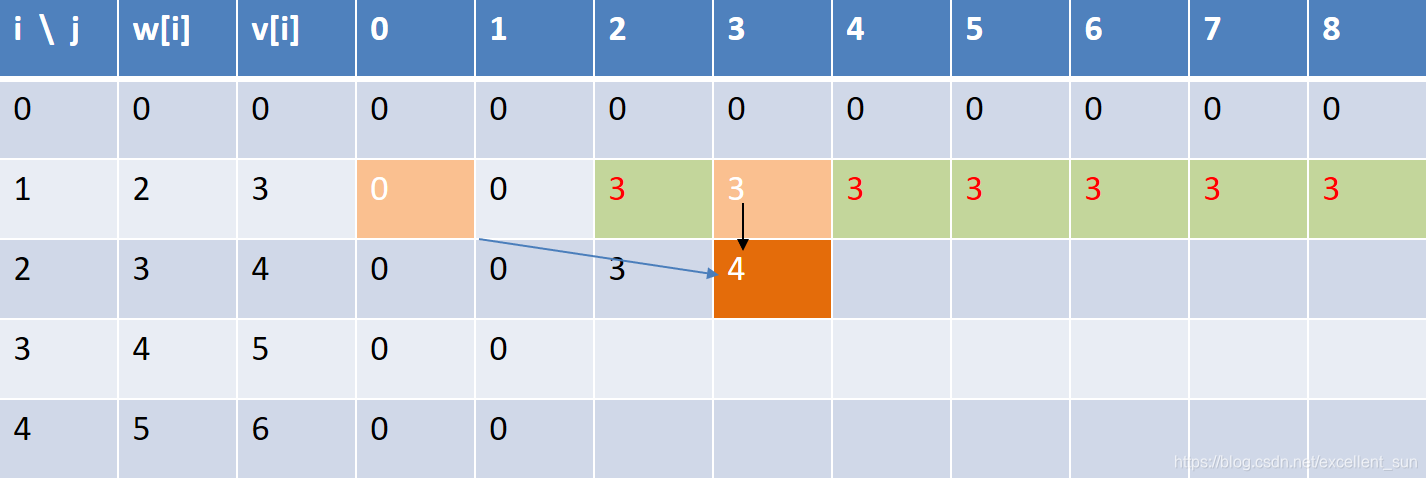
所以在枚举过程中仅用到上一行的数据，所以可以用一维数组来优化。

问题2 使用一维数组优化过程中为什么物体的重量要从大到小枚举？

我从大到小枚举如下：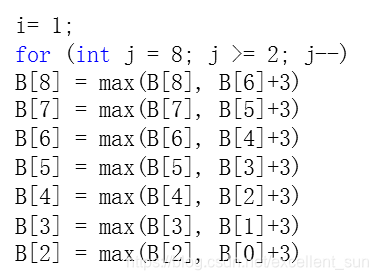


我从小到大枚举如下：

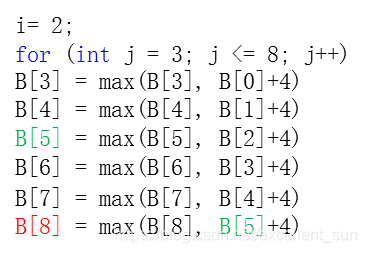
code1

#include<iostream>
#define N 6
#define W 21

int B[N][W] = { 0 };
int w[6] = { 0, 2, 3, 4, 5, 9 };
int v[6] = { 0, 3, 4, 5, 8, 10 };

void knapsack() {
	int k, C;
	for (k = 1; k < N; k++) {
		for (C = 1; C < W; C++) {
			if (w[k] > C) {
				B[k][C] = B[k - 1][C];
			}
			else {
				int value1 = B[k - 1][C - w[k]] + v[k];
				int value2 = B[k - 1][C];
				if (value1 > value2) {
					B[k][C] = value1;
				}
				else {
					B[k][C] = value2;
				}
			}
		}
	}
}
int main() {
	knapsack();
	printf("%d\n", B[5][20]);
	return 0;
}

code2

#include<iostream>
#include<algorithm>
#define N 1010
#define V 1010

using namespace std;

int n, m;
int B[N][N] = {0};
int v[N], w[N];
int main() {
	cin >> n >> m;
	for (int i = 1; i <=n; i++) cin >> v[i] >> w[i];
	
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			if (w[i] > j) {
				B[i][j] = B[i - 1][j];
			}
			else {
				B[i][j] = max(B[i - 1][j - w[i]] + v[i], B[i - 1][j]);
			}
		}
	}
	cout << B[n][m]  << endl;
	return 0;
}

code3

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 1010;

int n, m;
int B[N][N];
int value[N], weight[N];
int main() {
	cin >> n >> m;
	for (int i = 1; i <=n; i++) cin >> weight[i] >> value[i];
	
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			B[i][j] = B[i - 1][j];
			if(j >= weight[i])
				B[i][j] = max(B[i - 1][j - weight[i]] + value[i], B[i][j]);
		}
	}
	int res = 0;
	for (int i = 0; i <= m; i++) res = max(res, B[n][i]);
	cout << res << endl;
	return 0;
}

code（一维数组优化）

#include<iostream>
#include<algorithm>

using namespace std;

const int N = 1010;

int n, m;
int B[N];
int value[N], weight[N];
int main() {
	cin >> n >> m;
	for (int i = 1; i <=n; i++) cin >> weight[i] >> value[i];
	
	for (int i = 1; i <= n; i++) {
		for (int j = m; j >= weight[i]; j--) {
				B[j] = max(B[j - weight[i]] + value[i], B[j]);
		}
	}
	cout << B[m] << endl;
	system("pause");
	return 0;
}

来源：https://blog.csdn.net/excellent_sun/article/details/98998158