二叉查找树

一、定义

　　二叉查找(搜索)树(Binary Search Tree)。其定义为：二叉查找树或者是空树，或者是满足如下性质的二叉树：
①若它的左子树非空，则左子树上所有结点的值均小于根结点的值；
②若它的右子树非空，则右子树上所有结点的值均大于根结点的值；
③左、右子树本身又各是一棵二叉查找树。
　　上述性质简称二叉查找树性质(BST性质)，故二叉查找树实际上是满足BST性质的二叉树。

二、特点

　　由BST性质可得：
　　（1） 二叉查找树中任一结点x，其左(右)子树中任一结点y(若存在)的关键字必小(大)于x的关键字。
　　（2） 二叉查找树中，各结点关键字是惟一的。注意：实际应用中，不能保证被查找的数据集中各元素的关键字互不相同，所以可将二叉查找树定义中BST性质(1)里的"小于"改为"大于等于"，或将BST性质(2)里的"大于"改为"小于等于"，甚至可同时修改这两个性质。
　　（3） 按中序遍历该树所得到的中序序列是一个递增有序序列。如下图所示的两棵树均是二叉查找树，它们的中序序列均为有序序列：2，3，4，5，7，8。

　　　　　　　　

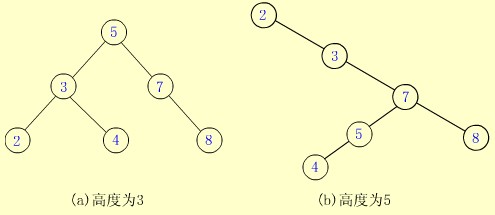
三、插入运算

　　在二叉查找树中插入新结点，要保证插入后仍满足BST性质。其插入过程是：
(a)若二叉查找树T为空，则为待插入的关键字key申请一个新结点，并令其为根；
(b)若二叉查找树T不为空，则将key和根的关键字比较：
 　　(i)若二者相等，则说明树中已有此关键字key，无须插入。
 　　(ii)若key<T→key，则将key插入根的左子树中。
 　　(iii)若key>T→key，则将它插入根的右子树中。
　　子树中的插入过程与上述的树中插入过程相同。如此进行下去，直到将key作为一个新的叶结点的关键字插入到二叉查找树中，或者直到发现树中已有此关键字为止。
注意：输入序列决定了二叉查找树的形态。二叉查找树的中序序列是一个有序序列。所以对于一个任意的关键字序列构造一棵二叉查找树，其实质是对此关键字序列进行排序，使其变为有序序列。因此，人们又常常将二叉查找树称为二叉排序树。通常将这种排序称为树排序(Tree Sort)，可以证明这种排序的平均执行时间亦为O(nlgn)。对相同的输入实例，树排序的执行时间约为堆排序的2至3倍。因此在一般情况下，构造二叉排序树的目的并非为了排序，而是用它来加速查找，这是因为在一个有序的集合上查找通常比在无序集合上查找更快，“查找树"的名称也由此而来。

　　　　　　

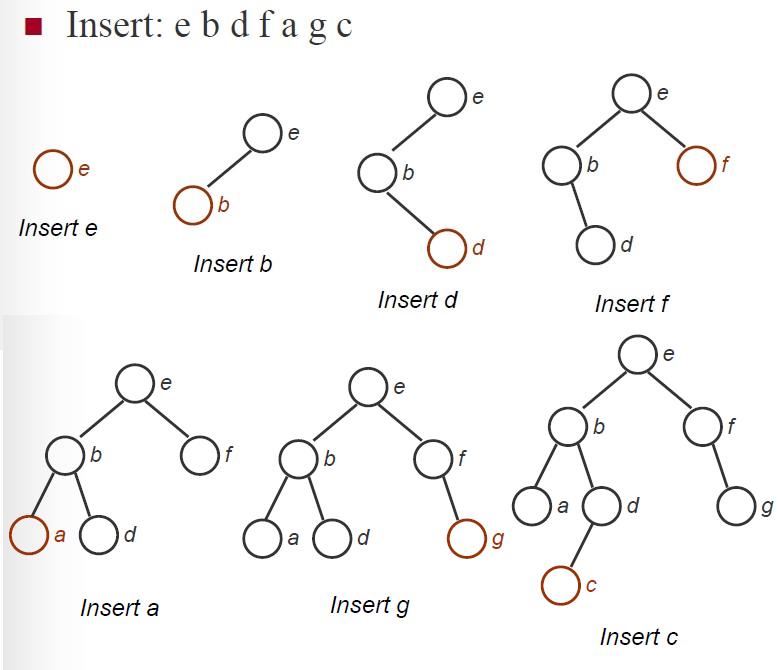
四、删除运算

　　从二叉查找树中删除一个结点，不能把以该结点为根的子树都删去，并且还要保证删除后所得的二叉树仍然满足BST性质。

一般步骤：
(a) 进行查找。查找时，令p指向当前访问到的结点，parent指向其双亲(其初值为NULL)。若树中找不到被删结点则返回，否则被删结点是p。
(b) 删去p。删去p时，应将p的子树(若有)仍连接在树上且保持BST性质不变。按p的孩子数目分三种情况进行处理。
　　　　(i)p是叶子(即它的孩子数为0)，无须连接p的子树，只需将p的双亲parent中指向p的指针域置空即可。
　　　　(ii)p只有一个孩子child，只需将child和p的双亲直接连接后，即可删去p。注意，p既可能是parent的左孩子也可能是其右孩子，而child可能是p的左孩子或右孩子，故共有4种状态。
　　　　(iii)p有两个孩子，先令q=p，将被删结点的地址保存在q中；然后找q的中序后继p，并在查找过程中仍用parent记住p的双亲位置。q的中序后继p一定是q的右子树中最左下的结点，它无左子树。因此，可以将删去q的操作转换为删去的p的操作，即在释放结点p之前将其数据复制到q中，就相当于删去了q。如下图BST中删除37：

　　　　　　

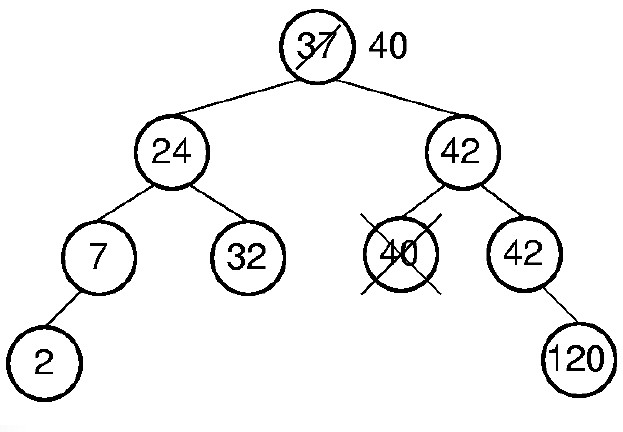
五、查找运算

　　在BST中查找一个值。如果树中的某个值与要查找的值相等，则返回这个结点，否则报告查找不成功。
　　进行查找时，先用目标值与树根的值相比较。如果相等，则找到；否则，如果目标值大于根的值，则继续在根的右子树中继续查找；如果目标值小于根的值，则继续在根的左子树中继续查找。
　　相同的关键字集合可能构成多棵不同的BST树。查找目标过程中，从根到目标结点之间的路径上的结点个数就是要进行比较的次数。树越平衡，要比较的次数越少。
　　如果二叉树接近平衡，则在树中查找一个结点时，需要进行的比较次数接近O(log n)。如果树退化为一个直链，则树的查找类似于顺序查找，其比较次数接近于O(n) ，这是树查找中的最坏时间复杂度。
　　一般不能预测要建立的二叉树的树型。实际上，如果关键字的排列是随机的，则建立的二叉树的树型将比较平衡，查找的效率接近二分查找。

六、平衡二叉树

    　为了保证二叉查找树的高度为lgn，从而保证然二叉查找树上实现的插入、删除和查找等基本操作的平均时间为O(lgn)，在往树中插入或删除结点时，要调整树的形态来保持树的“平衡”。使之既保持BST性质不变又保证树的高度在任何情况下均为O(lgn)，从而确保树上的基本操作在最坏情况下的时间均为O(lgn)。

注意：
　    ①平衡二叉树(Balanced Binary Tree)是指树中任一结点的左右子树的高度大致相同。
    　②任一结点的左右子树的高度均相同(如满二叉树)，则二叉树是完全平衡的。通常，只要二叉树的高度为O(1gn)，就可看作是平衡的。
    　③平衡的二叉查找树指满足BST性质的平衡二叉树。
    　④AVL树中任一结点的左、右子树的高度之差的绝对值不超过1。在最坏情况下，n个结点的AVL树的高度约为1.44lgn。而完全平衡的二叉树度高约为lgn，AVL树是接近最优的。

七、快速搜索磁盘文件

　　用二叉查找树解决快速搜索磁盘文件记录的代码如下：

代码

Code highlighting produced by Actipro CodeHighlighter (freeware)http://www.CodeHighlighter.com/-->    //定义索引文件结点的数据的类型
    public struct indexnode
    {
        int key;
        int offset;
        public indexnode(int key, int offset)
        {
            this.key = key;
            this.offset = offset;
        }
        //键属性 
        public int Key
        {
            get
            {
                return key;
            }
            set
            {
                value = key;
            }
        }
        //位置属性 
        public int Offset
        {
            get
            {
                return offset;
            }
            set
            {
                value = offset;
            }
        }
        public override string ToString()
        {
            return key + "," + offset;
        }
    }
    public class LinkBiSearchTree : LinkBiTree<indexnode>
    {
        //定义增加结点的方法
        public void insert(indexnode element)
        {
            Node<indexnode> tmp, parent = null, currentNode = null;
            //调用FIND方法
            find(element, ref parent, ref currentNode);
            if (currentNode != null)
            {
                Console.WriteLine("Duplicates words not allowed");
                return;
            }
            else
            {
                // 创建结点
                tmp = new Node<indexnode>(element);
                if (parent == null)
                    Head = tmp;
                else
                    if (element.Key < parent.Data.Key)
                        parent.LChild = tmp;
                    else
                        parent.RChild = tmp;
            }
        }
        //定位父结点
        public void find(indexnode element, ref Node<indexnode> parent, ref Node<indexnode> currentNode)
        {
            currentNode = Head;
            parent = null;
            while ((currentNode != null) && (currentNode.Data.ToString() != element.ToString()))
            {
                parent = currentNode;
                if (element.Key < currentNode.Data.Key)
                    currentNode = currentNode.LChild;
                else
                    currentNode = currentNode.RChild;
            }
        }
        //定位结点
        public void find(int key)
        {
            Node<indexnode> currentNode = Head;
            while ((currentNode != null) && (currentNode.Data.Key != key))
            {
                Console.WriteLine(currentNode.Data.Key);
                if (key < currentNode.Data.Key)
                    currentNode = currentNode.LChild;
                else
                    currentNode = currentNode.RChild;
            }
        }

        //主函数
        static void Main(string[] args)
        {
            LinkBiSearchTree b = new LinkBiSearchTree();
            while (true)
            {
                //菜单
                Console.WriteLine("\nMenu");
                Console.WriteLine("1. 创建二叉搜索树");
                Console.WriteLine("2. 执行中序遍历");
                Console.WriteLine("3. 执行前序遍历");
                Console.WriteLine("4. 执行后序遍历");
                Console.WriteLine("5. 显示搜索一个结点的路径");
                Console.WriteLine("6. exit");

                //接受用户选择
                Console.Write("\n 输入你的选择 (1-5):");
                char ch = Convert.ToChar(Console.ReadLine());
                Console.WriteLine();

                //对选择进行响应
                switch (ch)
                {
                    case '1':
                        {
                            int key, offset;
                            string flag;
                            do
                            {
                                Console.Write("请输入键:");
                                key = Convert.ToInt32(Console.ReadLine());
                                Console.Write("请输入位置:");
                                offset = Convert.ToInt32(Console.ReadLine());
                                indexnode elem = new indexnode(key, offset);
                                b.insert(elem);
                                Console.Write("继续添加新的结点吗(Y/N):");
                                flag = Console.ReadLine();
                            }
                            while (flag == "Y" || flag == "y");
                        }
                        break;
                    case '2':
                        {
                            b.inorder(b.Head);
                        }
                        break;
                    case '3':
                        {
                            b.preorder(b.Head);

                        }
                        break;
                    case '4':
                        {
                            b.postorder(b.Head);
                        }
                        break;
                    case '5':
                        {
                            int key;
                            Console.Write("请输入键:");
                            key = Convert.ToInt32(Console.ReadLine());
                            b.find(key);
                        }
                        break;
                    case '6':
                        return;
                    default:
                        {
                            Console.WriteLine("Invalid option");
                            break;
                        }
                }
            }
        }
    }

 

 原文：http://www.cnblogs.com/xiaosuo/archive/2010/02/10/1656183.html

转载于:https://www.cnblogs.com/Leo-Forest/archive/2012/11/12/2767191.html

来源：https://blog.csdn.net/weixin_30564901/article/details/99022672