1,概念
以下词条解释来自百度百科:代数,代数系统,线性代数,矩阵
代数
代数是研究数、数量、关系、结构与代数方程(组)的通用解法及其性质的数学分支。初等代数一般在中学时讲授,介绍代数的基本思想:研究当我们对数字作加法或乘法时会发生什么,以及了解变量的概念和如何建立多项式并找出它们的根。代数的研究对象不仅是数字,而是各种抽象化的结构。在其中我们只关心各种关系及其性质,而对于“数本身是什么”这样的问题并不关心。常见的代数结构类型有群、环、域、模、线性空间等。
代数系统
非空集合A和A上k个一元或二元运算f1,f2,…,fk组成的系统称为一个代数系统,简称代数,记作(A,f1,f2,…,fk)。由定义可知,一个代数系统需要满足下面3个条件:(1)有一个非空集合A;(2)有一些建立在集合A上的运算;(3)这些运算在集合A上是封闭的。有的书上对代数系统定义时不要求运算的封闭性,而是把具有封闭性的代数系统定义为一个新的概念-广群。
线性代数
线性代数是数学的一个分支,它的研究对象是向量,向量空间(或称线性空间),线性变换和有限维的线性方程组。向量空间是现代数学的一个重要课题;因而,线性代数被广泛地应用于抽象代数和泛函分析中;通过解析几何,线性代数得以被具体表示。线性代数的理论已被泛化为算子理论。由于科学研究中的非线性模型通常可以被近似为线性模型,使得线性代数被广泛地应用于自然科学和社会科学中。
矩阵
在数学中,矩阵(Matrix)是一个按照长方阵列排列的复数或实数集合 [1] ,最早来自于方程组的系数及常数所构成的方阵。
2,矩阵的基本运算
矩阵类
矩阵的信息有行数列数和矩阵的内容
struct matrix{
int n,m;
long long a[N][M];
matrix(){// 初始化2*2的单位矩阵
n=m=2;
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
a[i][j]=0;
}
}
for(int i=0;i<n;i++){
a[i][i]=1;
}
}
void clear(){
//memset(a,0,sizeof(a));
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
a[i][j]=0;
}
}
}
}
加和减
矩阵的加减运算要抱枕两个矩阵的行数和列数相同
matrix operator+(const matrix &b)const{
matrix tmp;
tmp.clear();
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
tmp.a[i][j]=a[i][j]+b.a[i][j];
}
}
return tmp;
}
乘法
设矩阵乘法的到的结果是矩阵S,则矩阵S的第i行第j个元素是被乘数的第i行元素乘以乘数的第j列元素的求和得到的,也就是说被乘数的列数和乘数的行数相等
matrix operator*(const matrix &b)const{
matrix tmp;
tmp.clear();
for(int i=0;i<n;i++){
for(int j=0;j<b.m;j++){
for(int k=0;k<m;k++){
tmp.a[i][j]=((a[i][k]*b.a[k][j])%mod+tmp.a[i][j])%mod;
}
}
}
return tmp;
}
因为乘法对矩阵有要求,所以矩阵乘法并不满足交换律,只满足结合律
除法
矩阵并没有除法运算,但是可以求逆,类似在初等数学中数的乘法逆元是他的倒数。矩阵的逆也满足这样的条件,1.矩阵S的逆的逆是矩阵S本身,2.除以矩阵S等于乘以矩阵S的逆
矩阵求逆代码:
vector<double> operator * (vector<double> a,double b){
int n=a.size();
vector<double> res(n,0);
for(int i=0;i<n;i++){
res[i]=a[i]*b;
}
return res;
}
vector<double> operator - (vector<double> a,vector<double> b){
int n=a.size();
vector<double> res(n,0);
for(int i=0;i<n;i++){
res[i]=a[i]-b[i];
}
return res;
}
void get_ni(vector<double>a[],vector<double>b[],int n){//b为初等变换所需要的单位矩阵
for(int i=0;i<n;i++){
b[i]=vector<double>(n,0);
}
for(int i=0;i<n;i++){//初始化单位矩阵
b[i][i]=1;
}
for(int i=0;i<n;i++){//初等变换
for(int j=i;j<n;j++){
if(fabs(a[j][i])>0){
swap(a[i],a[j]);
swap(b[i],b[j]);
break;
}
}
b[i]=b[i]*(1.0/a[i][i]);
a[i]=a[i]*(1.0/a[i][i]);
for(int j=0;j<n;j++){
if(j!=i&&fabs(a[j][i]>0)){
b[j]=b[j]-b[i]*a[j][i];
a[j]=a[j]-a[i]*a[j][i];
}
}i
}
}
3.高斯消元
4.常系数线性齐次递推
在求解斐波那契数列问题中,如果使用记忆化的技巧,在线性时间内就可以求解第n项斐波那契数是多少。
在矩阵中这个问题如何解决??
如果可以构造如图所示的矩阵,那么连续给矩阵乘以n个这样的矩阵就可以得到fn。
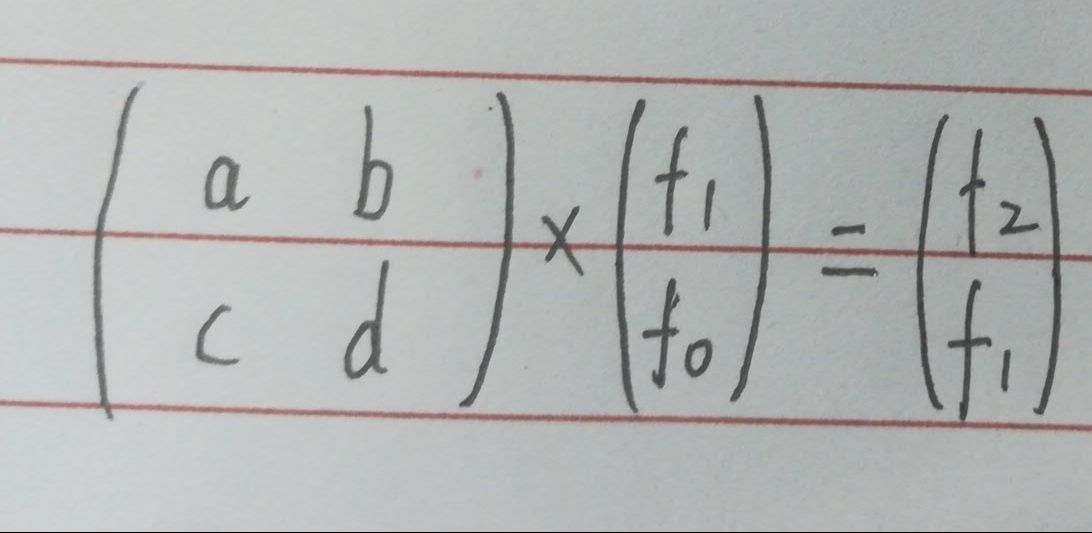
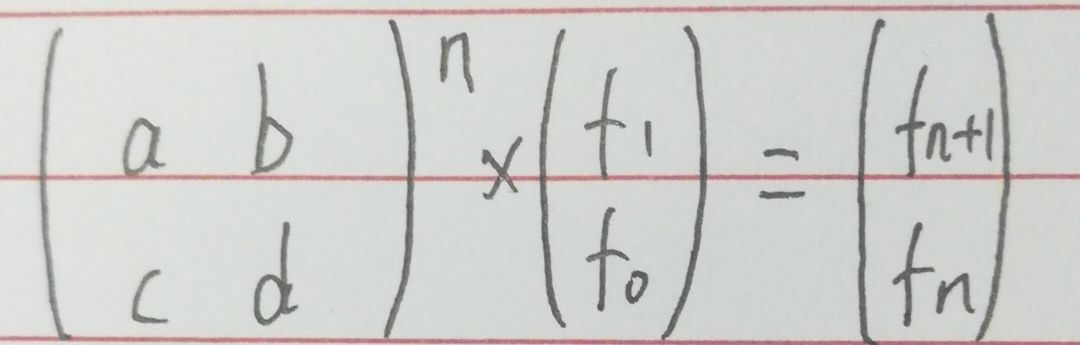
又因为矩阵满足结合律,所以可以用快速幂的方式,除去矩阵乘法的时间复杂度,O(logn)就可以得到斐波那契数列的第n项。
对于常系数线性齐次递推得到如下结论:
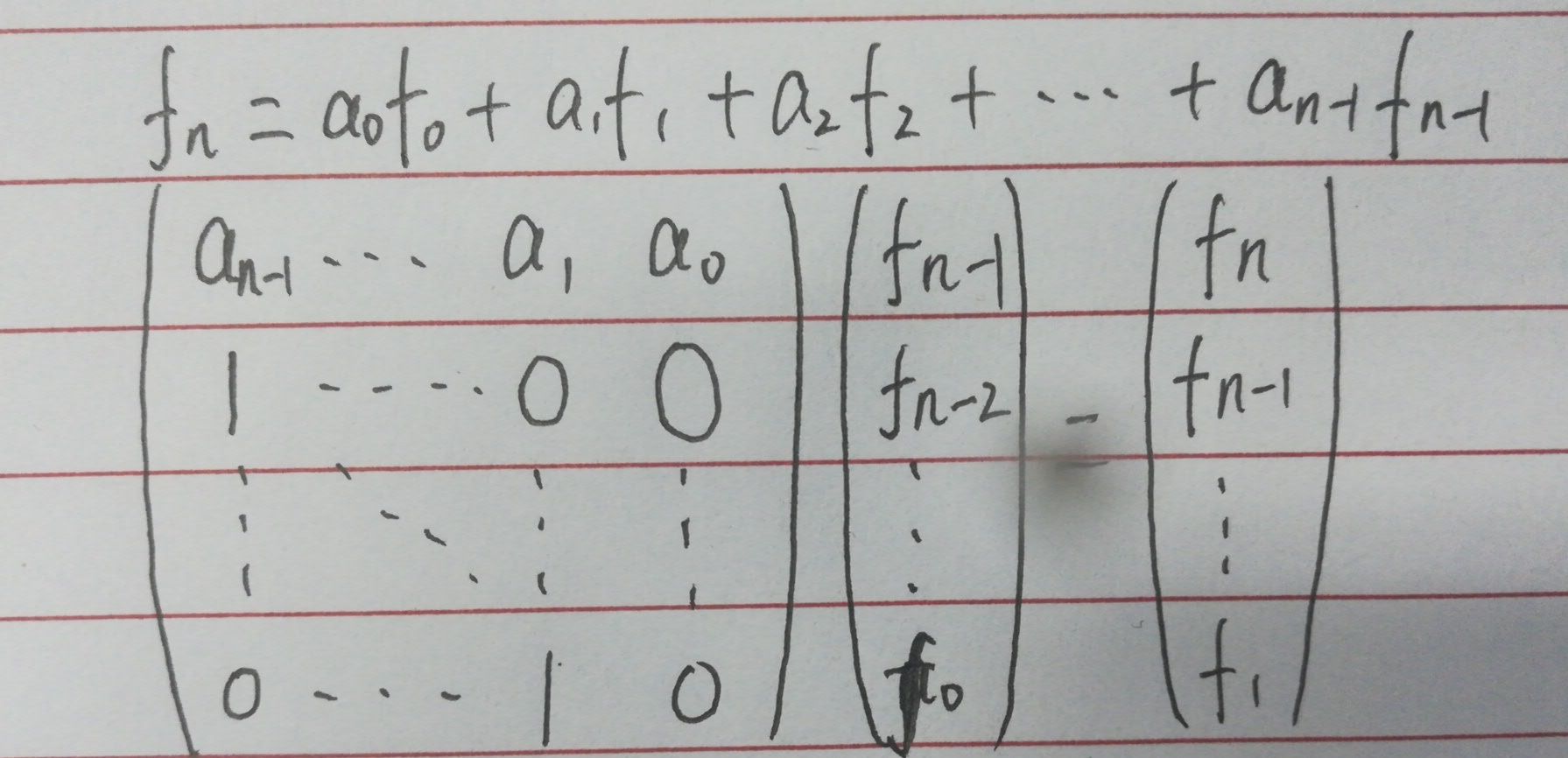
代码:
const int N=10,M=10;
long long a[10];
long long f[10];
struct matrix{
int n,m;
long long a[N][M];
matrix(){// 初始化2*2的单位矩阵
n=m=2;
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
a[i][j]=0;
}
}
for(int i=0;i<n;i++){
a[i][i]=1;
}
}
void clear(){
//memset(a,0,sizeof(a));
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
a[i][j]=0;
}
}
}
matrix operator+(const matrix &b)const{
matrix tmp;
tmp.clear();
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
tmp.a[i][j]=a[i][j]+b.a[i][j];
}
}
return tmp;
}
matrix operator*(const matrix &b)const{
matrix tmp;
tmp.clear();
for(int i=0;i<n;i++){
for(int j=0;j<b.m;j++){
for(int k=0;k<m;k++){
tmp.a[i][j]=((a[i][k]*b.a[k][j])+tmp.a[i][j]);
}
}
}
return tmp;
}
};
matrix pow2(matrix A,int n){
matrix B;
while(n>0){
if(n&1)B=B*A;
A=A*A;
n/=2;
}
return B;
}
long long solve(long long a[],long long f[],int n,int m){
matrix A,B;
A.clear();
B.clear();
A.n=B.n=n;
A.m=n;
B.m=1;
for(int i=0;i<n-1;i++){
A.a[i+1][i]=1;
}
for(int i=0;i<n;i++){
B.a[i][0]=f[n-i-1];
A.a[0][i]=a[n-i-1];
}
A=pow2(A,m);
B=A*B;
return B.a[n-1][0];
}
int main(){//求斐波那契数列第m项
a[0]=1,a[1]=1; //系数
f[0]=0,f[1]=1; //前n项
int m;
scanf("%d",&m);
printf("%lld\n",solve(a,f,2,m));
return 0;
}
一点心得:(走在路上啃馒头想到的(滑稽)
如果我们的递推式不仅仅是fn=an-1*fn-1+an-2*fn-2+………+a0*f0;这样简单的格式.而是fn=an-1*fn-1+an-2*fn-2+………+a0*f0+c;c是一个常数。那么可以构造如下的矩阵解决一个问题。

构造矩阵的方法或许没有多么巧妙,我却收获颇多。
1.矩阵乘法本身其实就在阐述一定的递推关系。
2.如果遇到下图所示矩阵,可分解为两个矩阵。
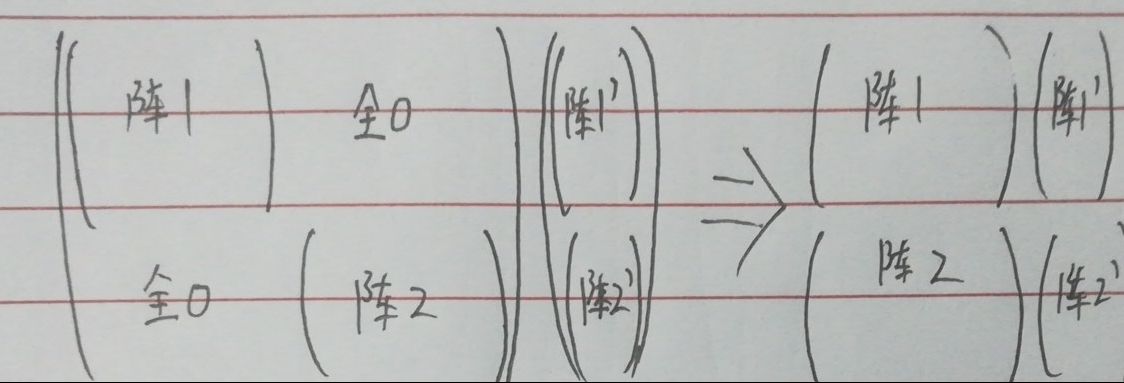
3.如果可以构造出f(n)=n的矩阵,则可以轻易得出fn=an-1*fn-1+an-2*fn-2+………+a0*f0+n的矩阵递推式
同理如果可以构造f(n)=an的矩阵,就可以轻易得出fn=an-1*fn-1+an-2*fn-2+………+a0*f0+an的矩阵递推式
结论:构造出的任意矩阵可以嵌套出一个新的递推式。