一、蚁群算法简介
二、TSP问题(旅行商问题)
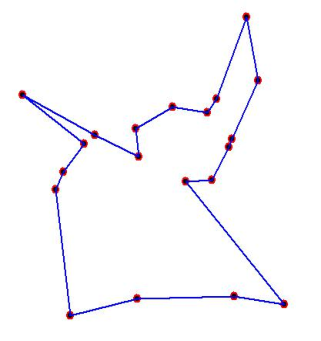
1、构建图:构建图与问题描述图是一致的,成份的集合C对应着点的集合(即:C=N),连接对应着边的集合(即L=A),且每一条边都带有一个权值,代表点i和j之间的距离。
2、约束条件:所有城市都要被访问且每个城市最多只能被访问一次。
3、信息素和启发式信息:TSP 问题中的信息素表示在访问城市i后直接访问城市j的期望度。启发式信息值一般与城市i和城市j的距离成反比。
4、解的构建:每只蚂蚁最初都从随机选择出来的城市出发,每经过一次迭代蚂蚁就向解中添加一个还没有访问过的城市。当所有城市都被蚂蚁访问过之后,解的构建就终止。
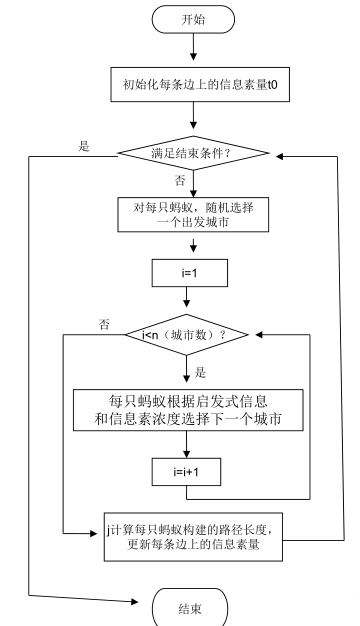

随机生成50个城市进行测试,初始蚂蚁数量为50,信息素重要程度因子alpha = 1,启发函数重要程度因子beta = 5,信息素挥发因子rho = 0.1,最大迭代次数为150
%% 旅行商问题(TSP)优化 %% 清空环境变量 clear all clc %% 导入数据 %load citys_data.mat city = ceil(rand(50,2) * 5000) load city.mat %% 计算城市间相互距离 fprintf('Computing Distance Matrix... \n'); n = size(city,1); D = zeros(n,n); for i = 1:n for j = 1:n if i ~= j D(i,j) = sqrt(sum((city(i,:) - city(j,:)).^2)); else D(i,j) = 1e-4; end end end %% 初始化参数 fprintf('Initializing Parameters... \n'); m = 50; % 蚂蚁数量 alpha = 1; % 信息素重要程度因子 beta = 5; % 启发函数重要程度因子 rho = 0.1; % 信息素挥发因子 Q = 1; % 常系数 Eta = 1./D; % 启发函数 Tau = ones(n,n); % 信息素矩阵 Table = zeros(m,n); % 路径记录表 iter = 1; % 迭代次数初值 iter_max = 150; % 最大迭代次数 Route_best = zeros(iter_max,n); % 各代最佳路径 Length_best = zeros(iter_max,1); % 各代最佳路径的长度 Length_ave = zeros(iter_max,1); % 各代路径的平均长度 %% 迭代寻找最佳路径 figure; while iter <= iter_max fprintf('迭代第%d次\n',iter); % 随机产生各个蚂蚁的起点城市 start = zeros(m,1); for i = 1:m temp = randperm(n); start(i) = temp(1); end Table(:,1) = start; % 构建解空间 city_index = 1:n; % 逐个蚂蚁路径选择 for i = 1:m % 逐个城市路径选择 for j = 2:n tabu = Table(i,1:(j - 1)); % 已访问的城市集合(禁忌表) allow_index = ~ismember(city_index,tabu); allow = city_index(allow_index); % 待访问的城市集合 P = allow; % 计算城市间转移概率 for k = 1:length(allow) P(k) = Tau(tabu(end),allow(k))^alpha * Eta(tabu(end),allow(k))^beta; end P = P/sum(P); % 轮盘赌法选择下一个访问城市 Pc = cumsum(P); target_index = find(Pc >= rand); target = allow(target_index(1)); Table(i,j) = target; end end % 计算各个蚂蚁的路径距离 Length = zeros(m,1); for i = 1:m Route = Table(i,:); for j = 1:(n - 1) Length(i) = Length(i) + D(Route(j),Route(j + 1)); end Length(i) = Length(i) + D(Route(n),Route(1)); end % 计算最短路径距离及平均距离 if iter == 1 [min_Length,min_index] = min(Length); Length_best(iter) = min_Length; Length_ave(iter) = mean(Length); Route_best(iter,:) = Table(min_index,:); else [min_Length,min_index] = min(Length); Length_best(iter) = min(Length_best(iter - 1),min_Length); Length_ave(iter) = mean(Length); if Length_best(iter) == min_Length Route_best(iter,:) = Table(min_index,:); else Route_best(iter,:) = Route_best((iter-1),:); end end % 更新信息素 Delta_Tau = zeros(n,n); % 逐个蚂蚁计算 for i = 1:m % 逐个城市计算 for j = 1:(n - 1) Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q/Length(i); end Delta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q/Length(i); end Tau = (1-rho) * Tau + Delta_Tau; % 迭代次数加1,清空路径记录表 % figure; %最佳路径的迭代变化过程 [Shortest_Length,index] = min(Length_best(1:iter)); Shortest_Route = Route_best(index,:); plot([city(Shortest_Route,1);city(Shortest_Route(1),1)],... [city(Shortest_Route,2);city(Shortest_Route(1),2)],'o-'); pause(0.3); iter = iter + 1; Table = zeros(m,n); % end end %% 结果显示 [Shortest_Length,index] = min(Length_best); Shortest_Route = Route_best(index,:); disp(['最短距离:' num2str(Shortest_Length)]); disp(['最短路径:' num2str([Shortest_Route Shortest_Route(1)])]); %% 绘图 figure(1) plot([city(Shortest_Route,1);city(Shortest_Route(1),1)],... [city(Shortest_Route,2);city(Shortest_Route(1),2)],'o-'); grid on for i = 1:size(city,1) text(city(i,1),city(i,2),[' ' num2str(i)]); end text(city(Shortest_Route(1),1),city(Shortest_Route(1),2),' 起点'); text(city(Shortest_Route(end),1),city(Shortest_Route(end),2),' 终点'); xlabel('城市位置横坐标') ylabel('城市位置纵坐标') title(['蚁群算法优化路径(最短距离:' num2str(Shortest_Length) ')']) figure(2) plot(1:iter_max,Length_best,'b',1:iter_max,Length_ave,'r:') legend('最短距离','平均距离') xlabel('迭代次数') ylabel('距离') title('各代最短距离与平均距离对比') 五、实验结果:
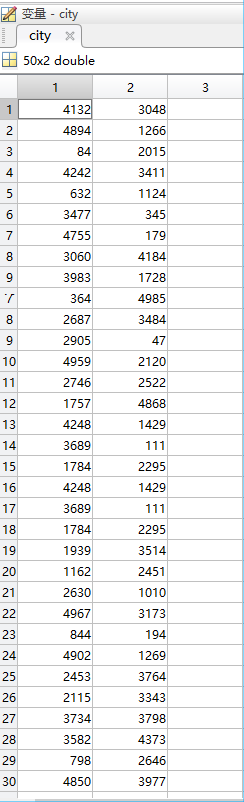
5.1随机生成的50个城市坐标



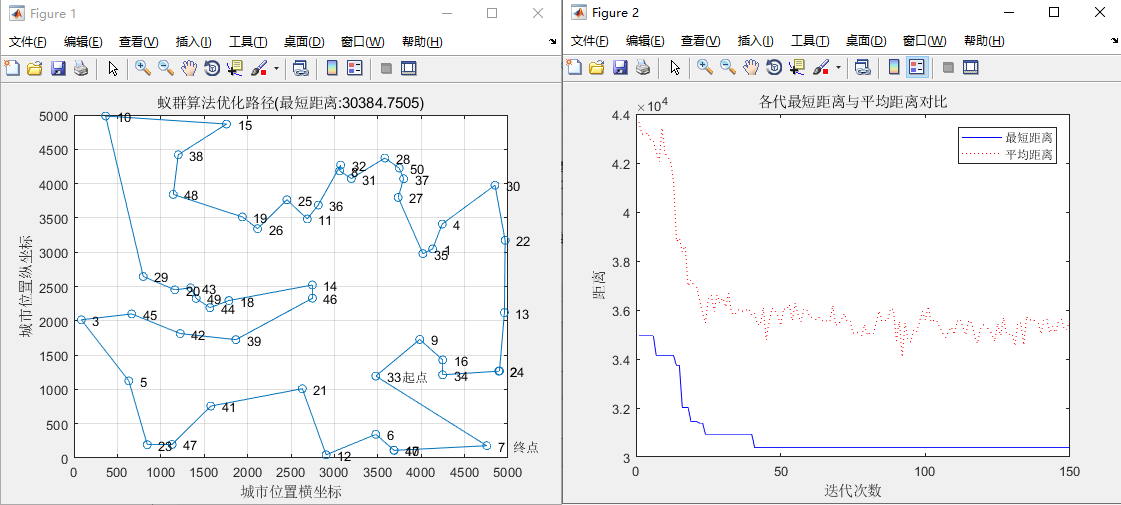
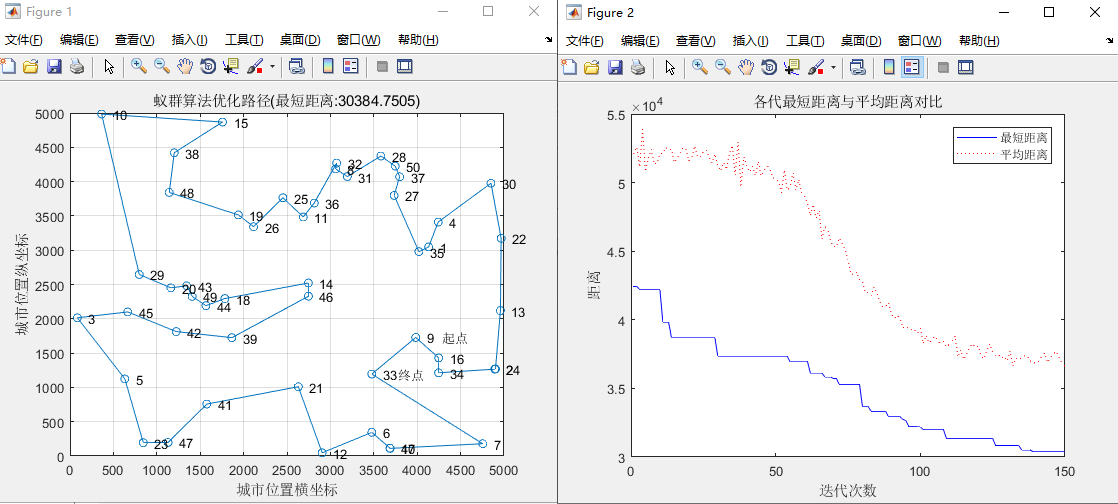
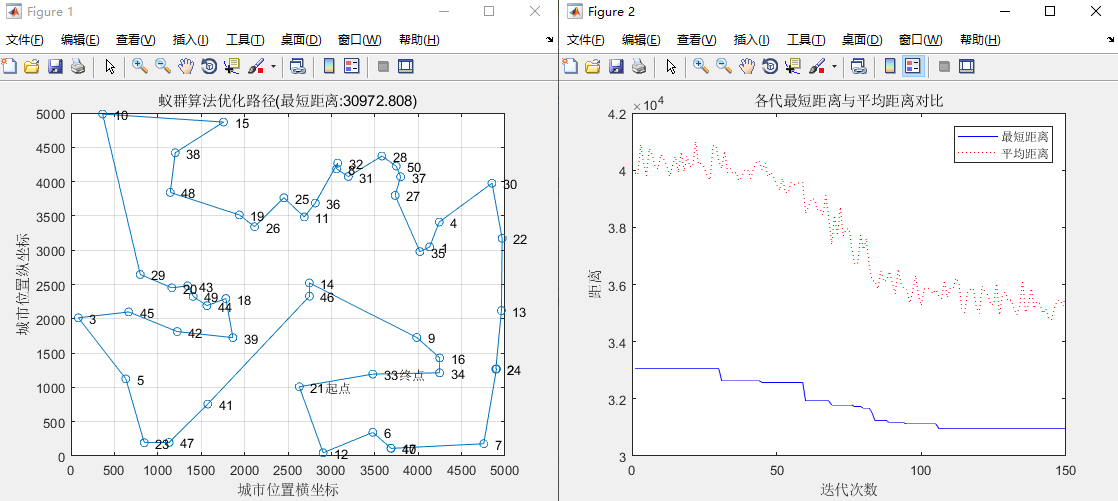
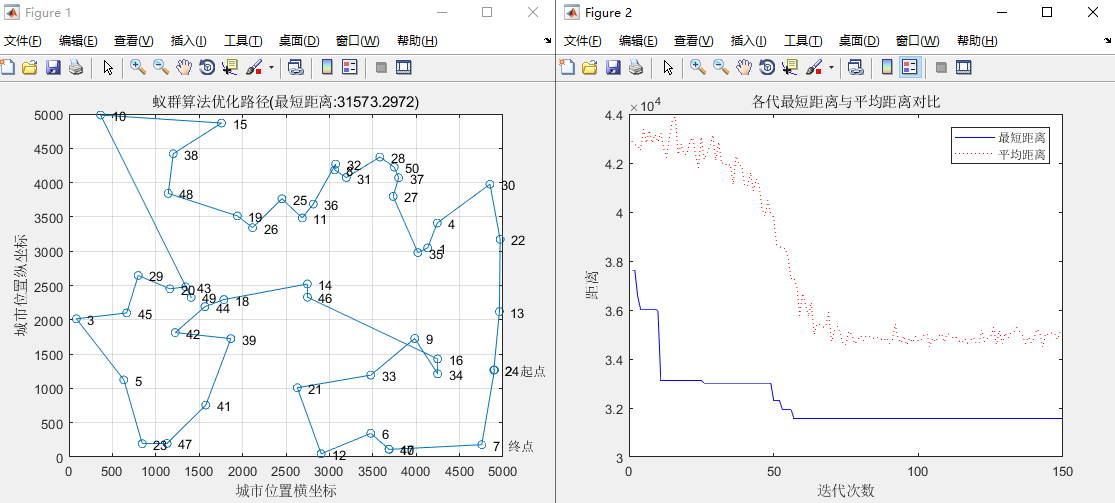
六、结果分析与总结
1、 蚂蚁数量、信息素重要程度因子、启发函数重要程度因子beta、最大迭代次数相同时,rho=0.1与rho=0.5
2、Bete=5与Bete=3、bete=7
3、alpha=1与alpha=4
来源:博客园
作者:积极废人
链接:https://www.cnblogs.com/twzh123456/p/11798800.html