对于特征很多的情况,采用 polynomial regression 多项式回归会产生指数型的时间复杂度。O(n^3)(次方数=多项式多少阶)
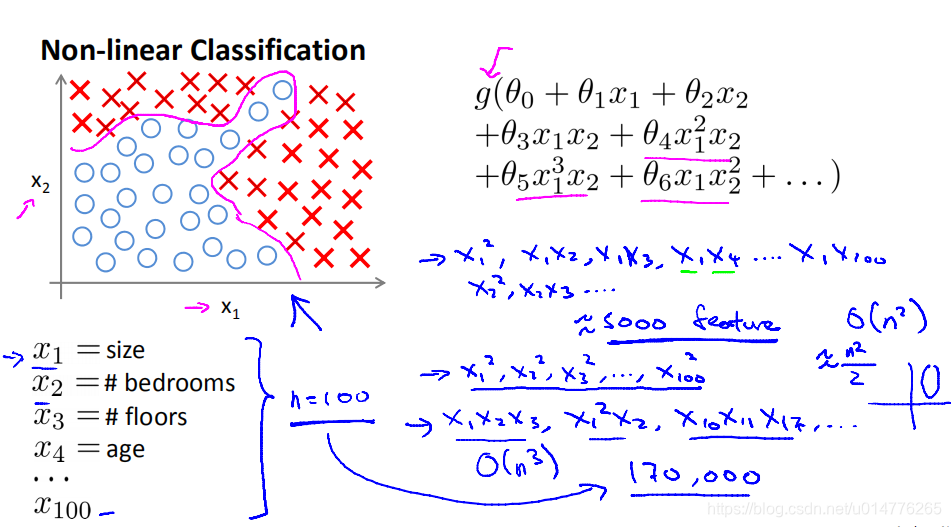
图像特征处理:
按像素点处理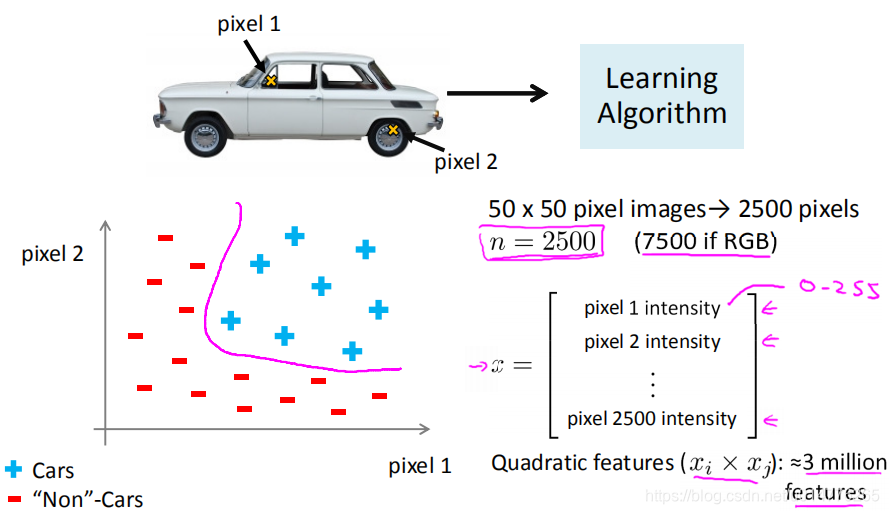
练习题:

选择(C)像素点共有100100=110^4 quadratic terms 平方项为n2/2时间复杂度为o(n2) 故 (104)2/2=5*10^7
神经网络原理:
将听觉的脑皮层,连接到视觉信号,听觉脑皮层 可以变成处理视觉的,看到图像。表明人的大脑神经原都是同一套,经过训练可以完成不同任务。故神经网络只需编写一套代码,来模拟神经。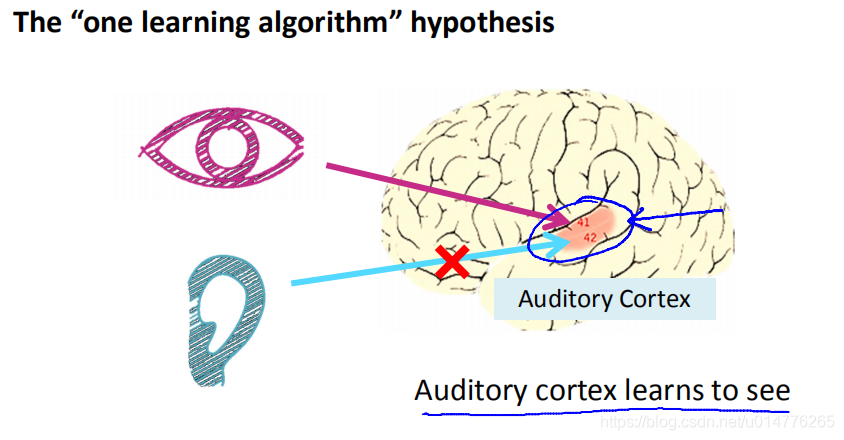
神经网络介绍:
x0叫做bias unit偏置单元,且x0=1,根据模型情况添加。
逻辑回归中的sigmod叫激活函数。
其中θ叫做参数,也叫作权重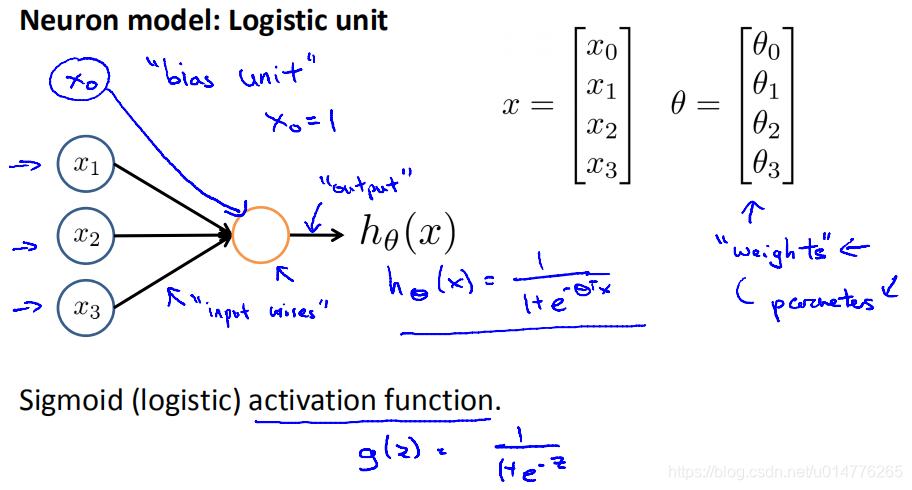
Layer1 叫做输入层,里面是[x0…xn]各个特征(x0不一定有)
Layer2:叫做隐含层,负责计算
Layer3:叫做输出层,输出结果给激活函数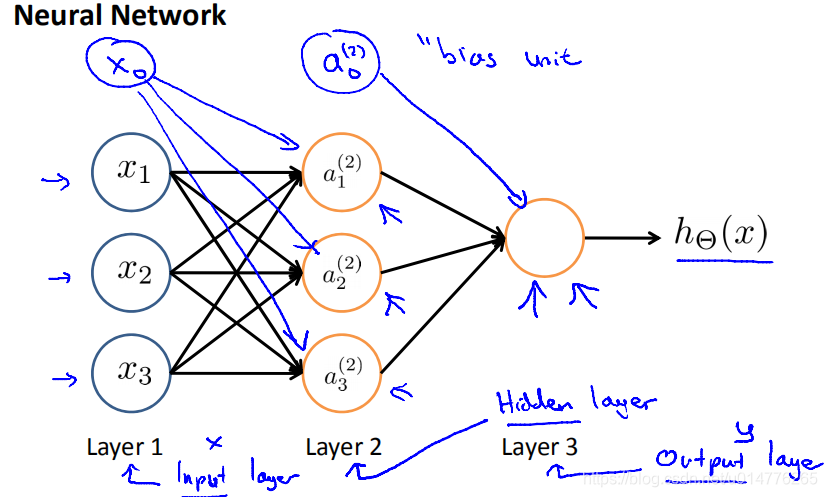
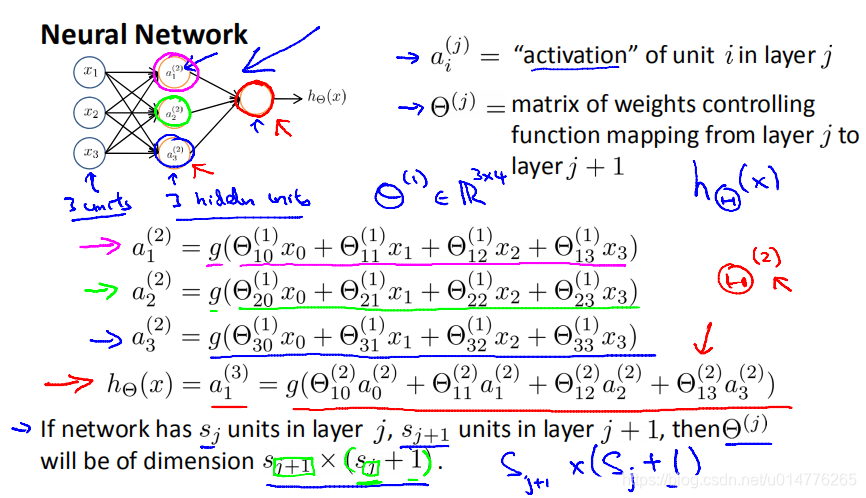
θ(j)多少维度:
后一层的数量*(前一层的数量+1)
θ(1)=R3*4
解释:
j+1中的+1来自bias nodes 偏置单元,
,也就是说输出节点将不包括偏置单元,而输入将包括偏置单元。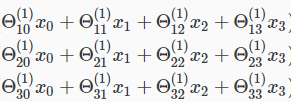
练习题:
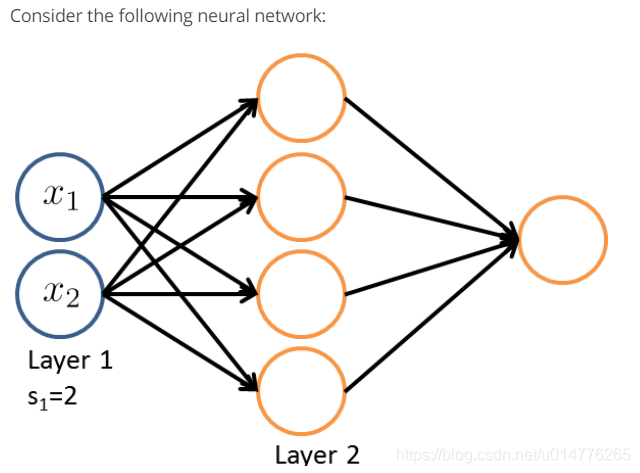

选择(D)sj+1=4 ,sj=2
故矩阵为4,2+1=[4,3]维矩阵
Forward propagation正向传播:
从输入层到隐含层,最后到输出层
z1(2)=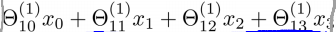
z(2)=Θ(1)*x=Θ(1)*a(1)
a(2)=g(z(2))
增加a0(2)=1 此时a(2)矩阵变为4维 R^4
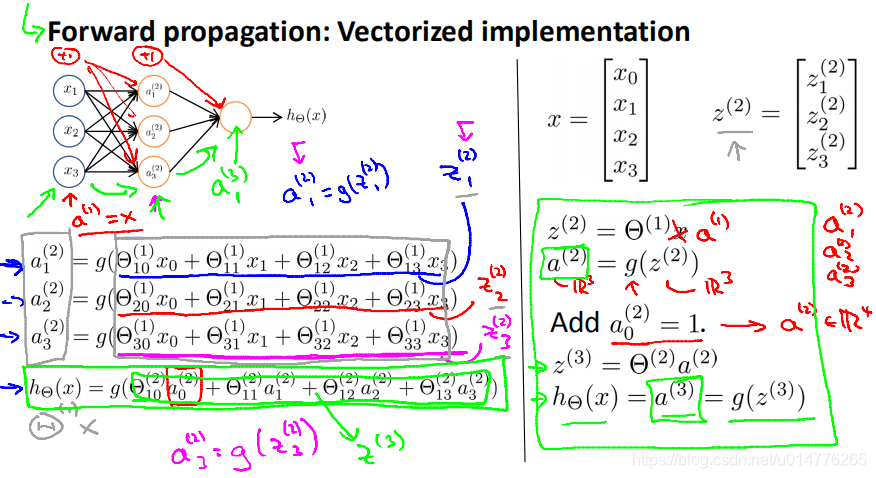
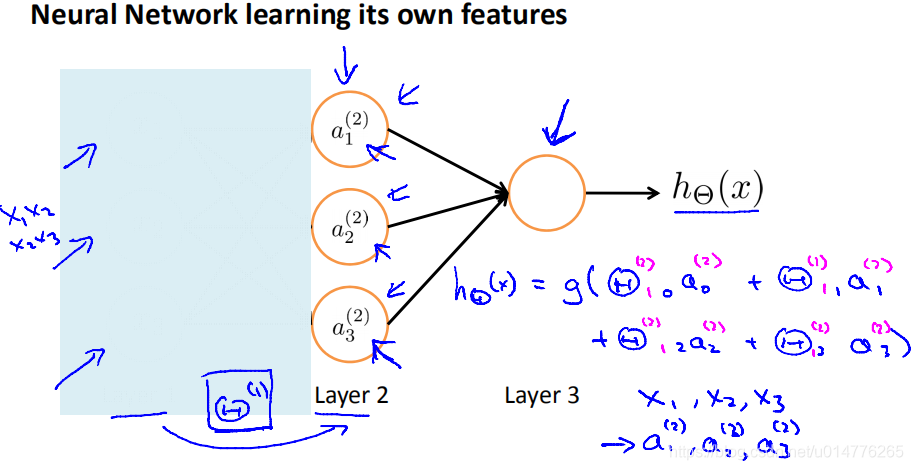
神经网络隐含层到输出层相当于从自己生成的特征中学习
neural network architecture神经网络结构
展示神经网络中各个神经元之间如何连接的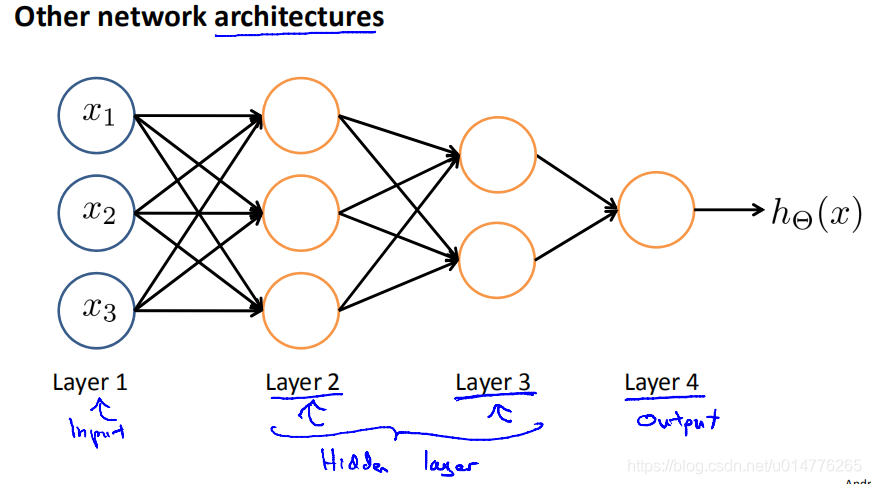
测试题:
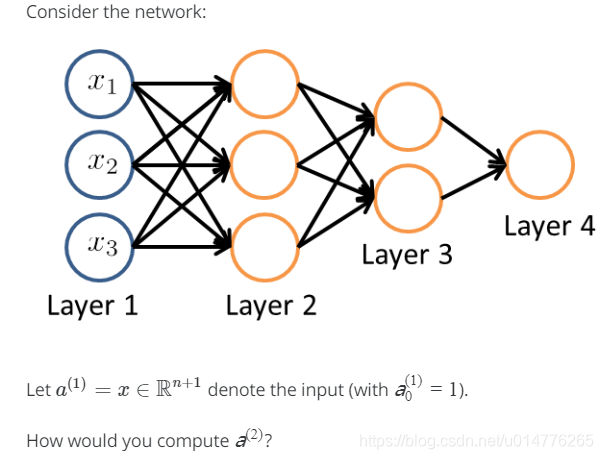
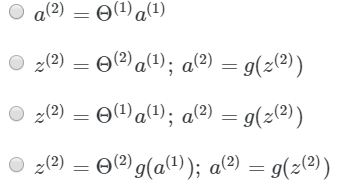
选择(C),由于中间的Θ为第一个,故为Θ1。
公式总结:
不增加bias unit偏置单元时的公式: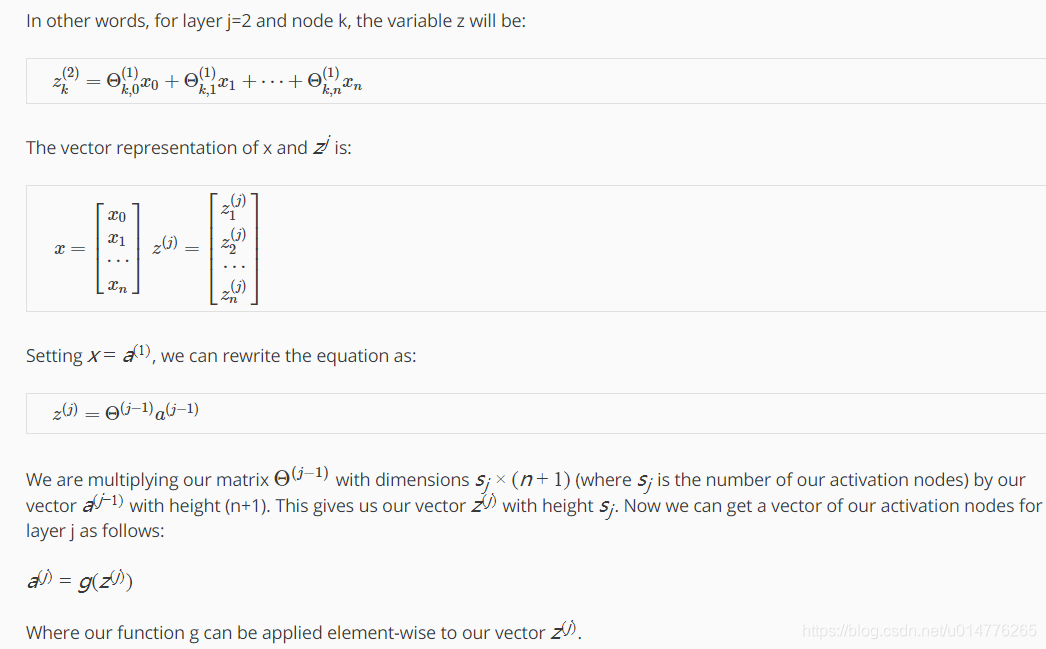
增加bias unit偏置单元时的公式:
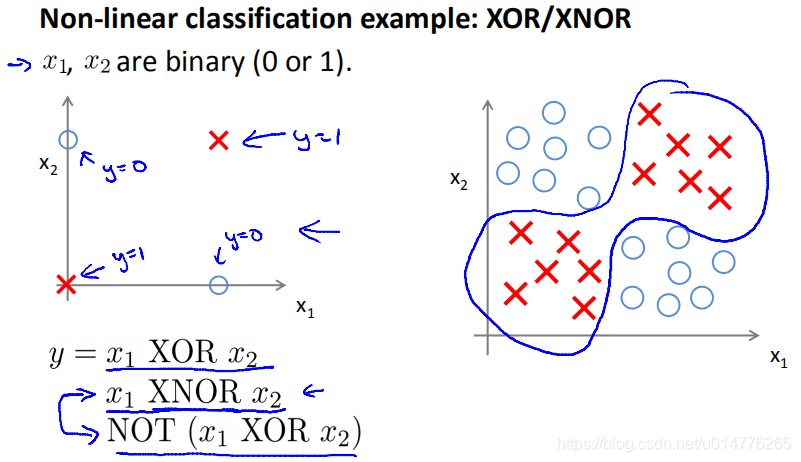
XOR异或,不相同的时候为1,相同为0
XNOR同或,相同为1,不相同为0
模拟AND且运算:
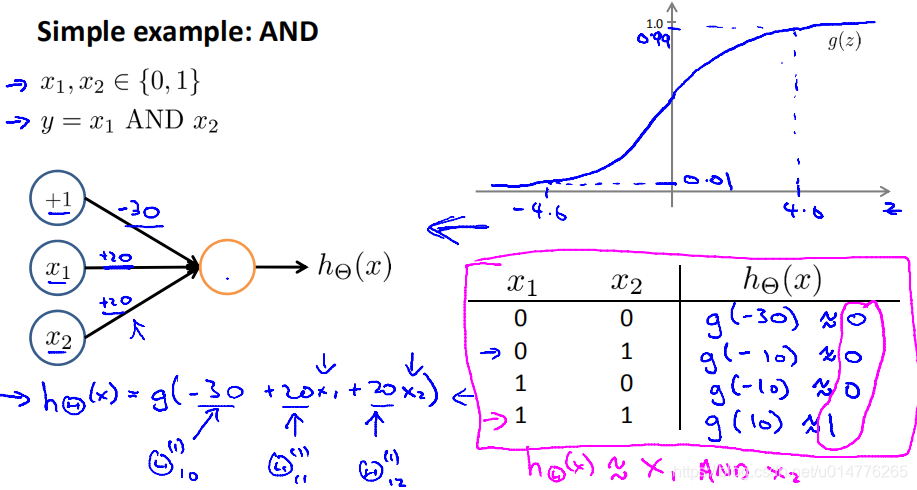
练习题:

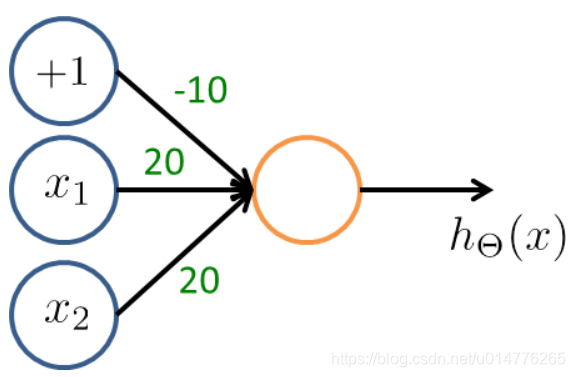

选择(C)
| x1 | x2 | 结果 |
|---|---|---|
| 0 | 0 | g(-10)≈0 |
| 0 | 1 | g(10)≈1 |
| 1 | 0 | g(10)≈1 |
| 1 | 1 | g(30)≈1 |
模拟OR或运算:

练习题:
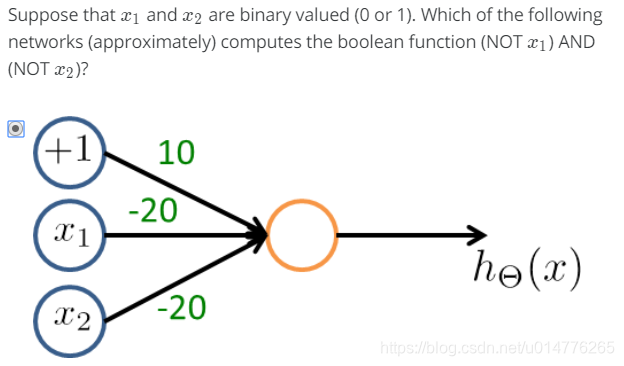
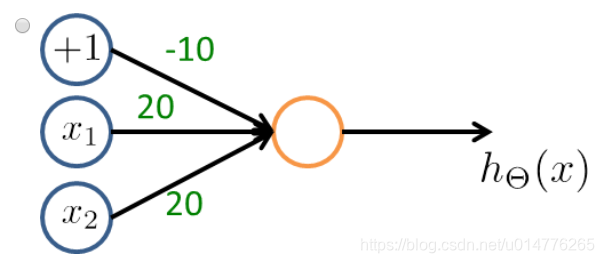
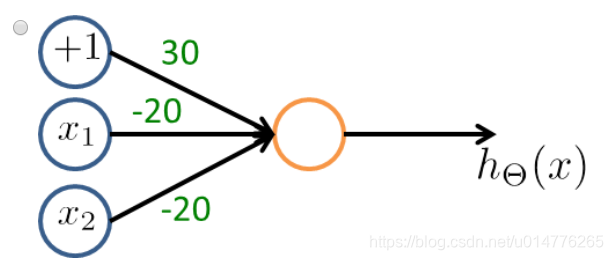
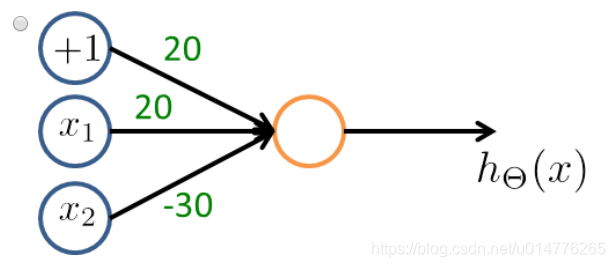
选择(A),否定哪一项 其系数应该为负数。NOTx1,故x1,x2项系数为负。然后A,C中代入尝试。
模拟XNOR或运算:
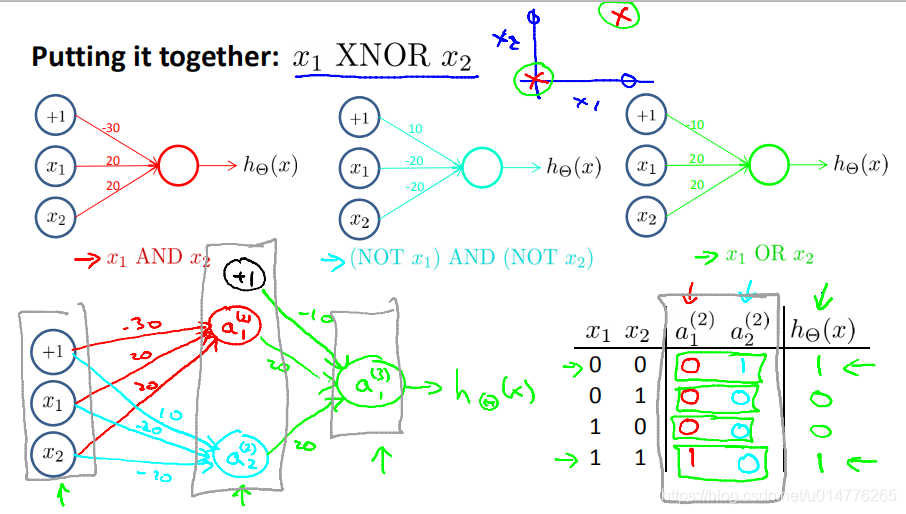
多分类问题:
原来的数据集y=1或者2或者3或者4,也就是输出一个数字。
现在神经网络输出一个向量。
标定数据集y(i)变成其中一种类别的向量。
如y(1)=[1,0,0,0]表示行人
y(2)=[0,1,0,0]表示汽车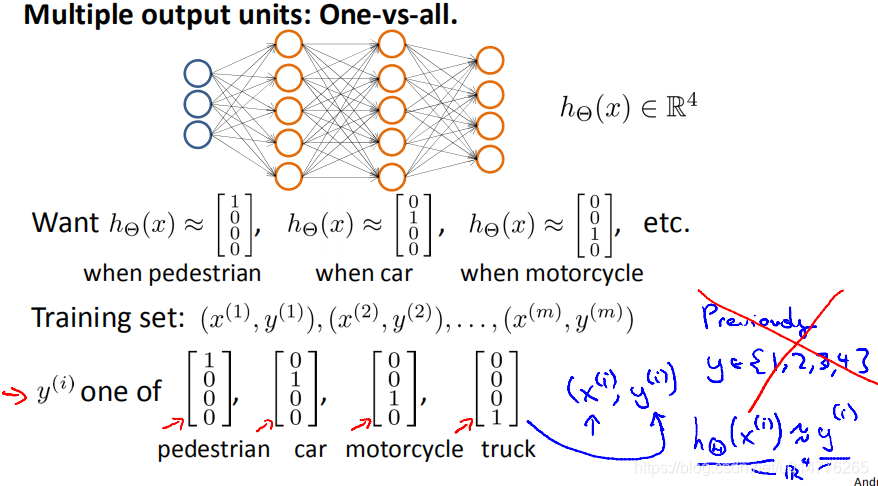
测试题:

选择(A,C)
B.XOR需要隐含层才能表示
C.每一层的激活值都要进入sigmod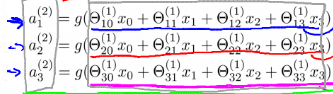
D.不对,因为每个a都是由前面的节点计算而来,同层之间的节点互不影响,只有加上softmax才有影响。
且对于多分类神经网络其输出为向量。如[0,0,1]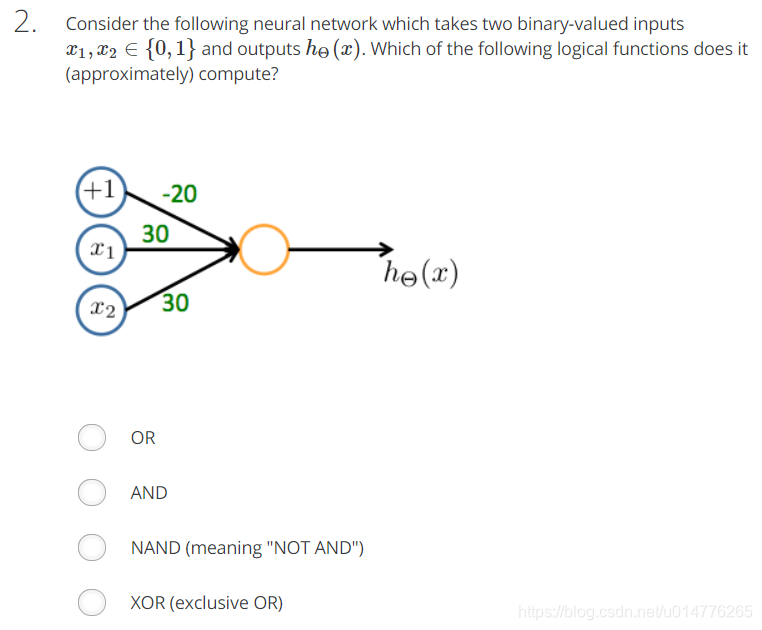
选择(A)
| x1 | x2 | 结果 |
|---|---|---|
| 0 | 0 | g(-20)≈0 |
| 0 | 1 | g(10)≈1 |
| 1 | 0 | g(10)≈1 |
| 1 | 1 | g(40)≈1 |
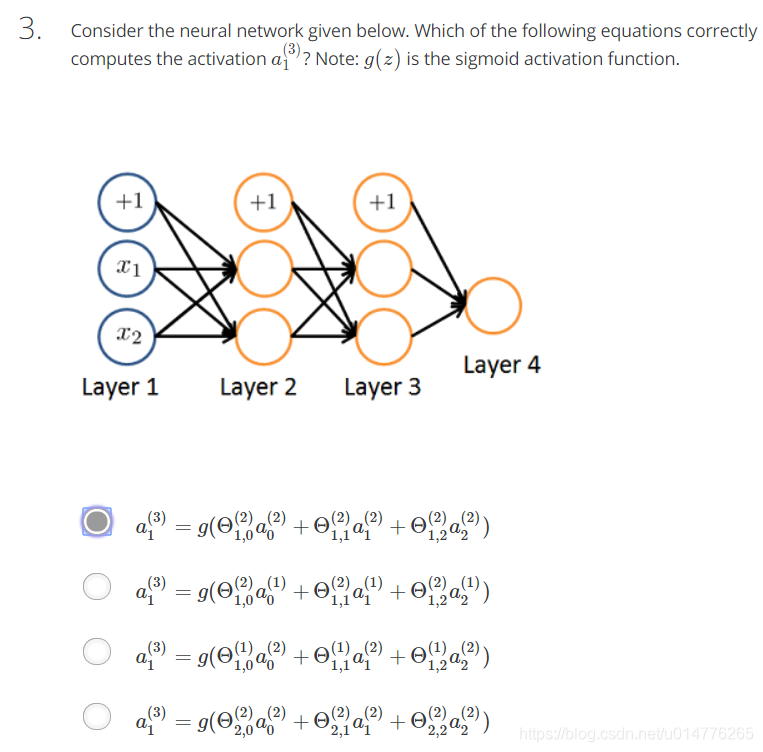
选择(A)
- a(3)1 是第3层的第1个激活单元=第2层的Θ 乘以 第2层的a *
- 第2层的Θ就是Θ2 *
- 第2层的a就是a2 *
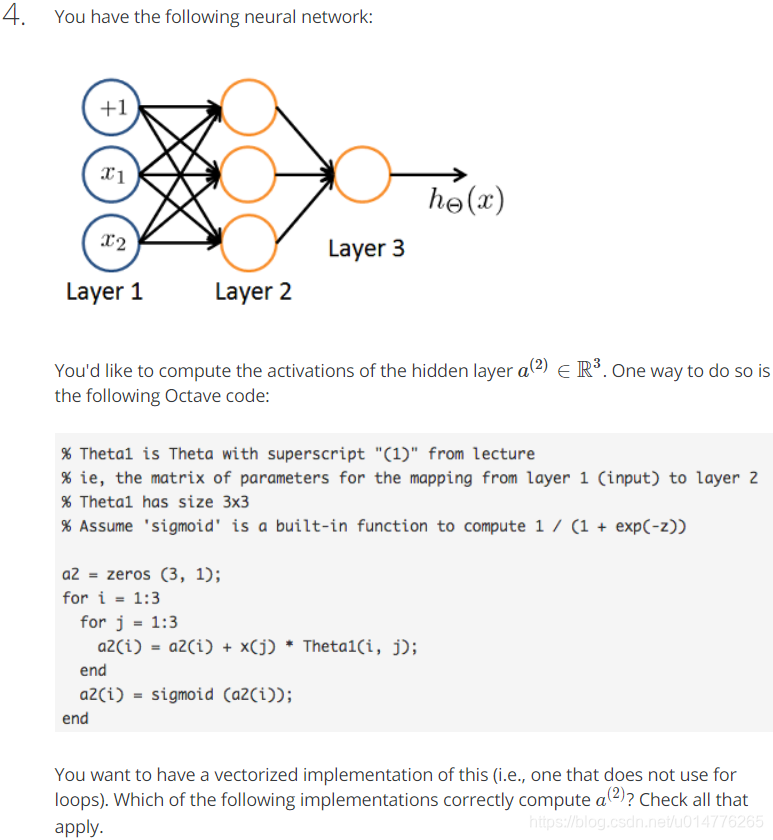

选择(A)
a(1)=input层x向量
a(2)=hidden layer隐含层
a(3)=hΘ(x)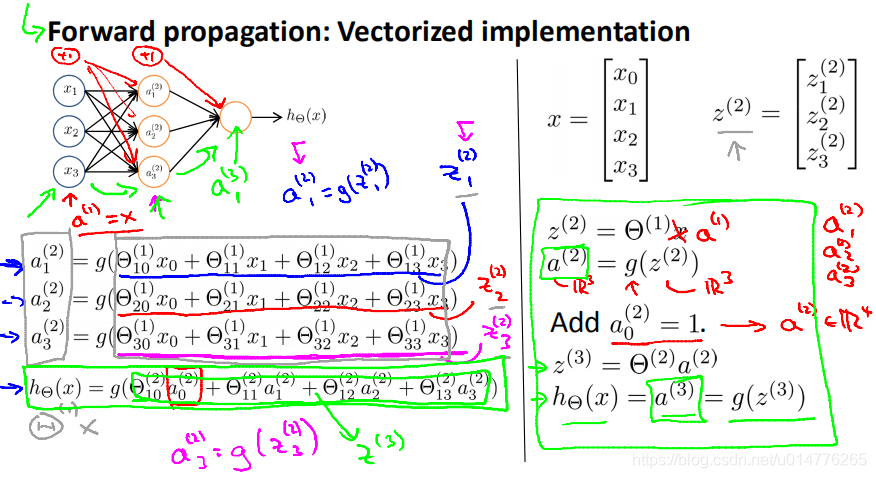
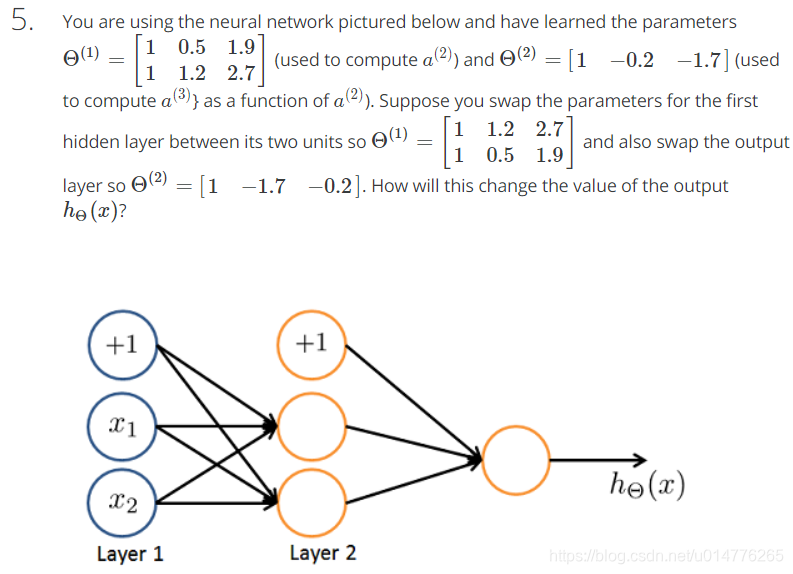
选择(A),相当于神经元都一样,换个参数,总体不变。当交换Θ(1)中的两行时,实际上就是交换了a(2)2 与 a(2)3, 最后算式不变。