Ŀ¼
1. 什么是智能优化算法
启发式算法,是一种具有全局优化性能、通用性强且适用于并行处理的算法。这种算法一般具有严密的理论依据,而不是单纯凭专家经验,理论上可以在一定的时间内找到最优解或近似最优解。
补充说明:
启发式算法(Heuristic Algorithm)有两种定义:
(1)基于直观或经验的构造的算法,对优化问题的实例能给出可接受的计算成本(计算时间、占用空间等)内,给出一个近似最优解,该近似解于真实最优解的偏离程度不一定可以实现预计;
(2)启发式算法是一种技术,这种技术使得在可接受的计算成本内去搜寻最好的解,但不一定保证所得的解是可行解和最优解,甚至在多数情况下,无法阐述所得解同最优解的近似程度。
总之,启发式算法可用于解决求解最优解代价比较大的问题,但是此类算法不保证得到最优解,求解结果不稳定且算法效果依赖于实际问题和设计者的经验。
2. 常用的智能优化算法
- 遗传算法(Genetic Algorithm, GA)
- 模拟退火算法(Simulated Annealing, SA)
- 禁忌搜索算法(Tabu Search, TS)
- 神经网络 (Neural Network)
- 蚁群算法(Ant Colony Optimization,ACO)
3. 智能优化算法的特点
二、模拟退火算法
1. 简介
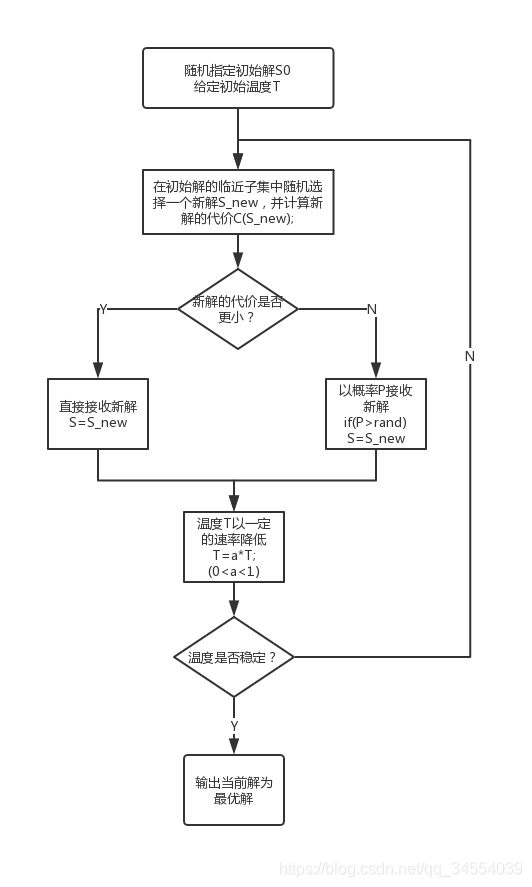
2.算法思想及步骤
 为所有的可能解,
为所有的可能解, 反映了取
反映了取 。
。 

其中,P为算法选择较差解的概率;T 为温度的模拟参数;
 。
。 - 当T很大时,
 ,此时算法以较大概率选择非当前最优解;
,此时算法以较大概率选择非当前最优解; - P的值随着T的减小而减小;
- 当
 时,
时, ,此时算法几乎只选择最优解,等同于贪心算法。
,此时算法几乎只选择最优解,等同于贪心算法。
三、MATLAB代码
例1. 求解函数的最小值问题
 ,其中
,其中 ,求解函数的最小值。
,求解函数的最小值。 %%main.m T=1000; %初始化温度值 T_min=1e-12; %设置温度下界 alpha=0.98; %温度的下降率 k=1000; %迭代次数(解空间的大小) x=getX; %随机得到初始解 while(T>T_min) for I=1:100 fx=Fx(x); x_new=getX; if(x_new>=-2 && x_new<=2) fx_new=Fx(x_new); delta=fx_new-fx; if (delta<0) x=x_new+(2*rand-1); else P=getP(delta,T); if(P>rand) x=x_new; end end end end T=T*alpha; end disp('最优解为:') disp(x) %%getX.m function x=getX x=4*rand-2; end %%Fx.m function fx=Fx(x) fx=(x-2)^2+4; end %%getP.m function p=getP(c,t) p=exp(-c/t); end 例2. 旅行商(TSP)问题
文章来源: https://blog.csdn.net/qq_34554039/article/details/90294046
 ,此时算法以较大概率选择非当前最优解;
,此时算法以较大概率选择非当前最优解; 时,
时, ,此时算法几乎只选择最优解,等同于贪心算法。
,此时算法几乎只选择最优解,等同于贪心算法。