工程应用常涉及三角函数的快速计算。设计者往往需要降低运算精度以提高程序的运行速度。常用的快速三角函数算法主要包括CORDIC、泰勒展开式逼近、查表等等。然而,网上的文章大多只介绍如何实现相应的算法,而忽视了定量分析算法精度并以此指导设计的过程。此外,算法不同,误差分析的数学方法也不尽相同。在多种算法之间比较时,需要耗费一些时间来建立模型。如果建立一个通用的误差分析框架,框架不局限于现存的几类算法,并且实现自动化的筛选,则有可能提高工作效率。
本文试图从开发者的角度,介绍一种通用的数值型误差分析框架,并以泰勒展开算法为例分析了其展开式项数与精度之间的定量关系,最终试图通过这些工作为快速三角函数算法的设计提供一定参考。
一、快速三角函数算法的原理分析
1. 预处理
对三角函数求值应充分考虑函数本身的性质。首先是周期性:正余弦函数的周期为2π,自变量的所有取值均可变换到单个周期[0, 2π]内,而使因变量保持不变;其次是对称性:例如正弦函数[0, π]上的图像与[π, 2π]上的图像关于X轴对称。取其中一支[0, π],还可以发现[0, π/2]与[π/2, π]上的图像关于平行Y轴的直线x = π/2对称。同理余弦函数也满足类似的性质。
综合上述性质可知,对于某个三角函数,若已知其在[0, π/2]的函数关系及必要的对称关系,则可通过恒等变换表示该三角函数在整个定义域上的取值。
设待求三角函数为f(x),f(x)在[0, π/2]的函数关系为g(x)。上述求值方法可表示为
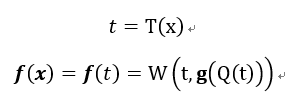
其中,函数T(t)表示将t变换到单个周期内;函数W(t,y)表示根据t取值,对三角函数的因变量y进行正负变换(即关于X轴对称的象限变换);函数Q(t)表示对t进行关于直线t = π/2的对称变换。
以f(x)=sin x为例说明,W(y,x)、Q(x)、T(x)三个变换函数的定义如下:
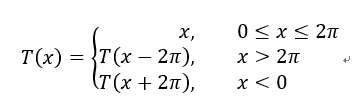
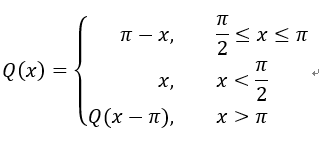
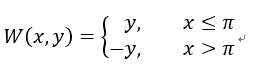
下图形象地描述了各变换函数的作用。
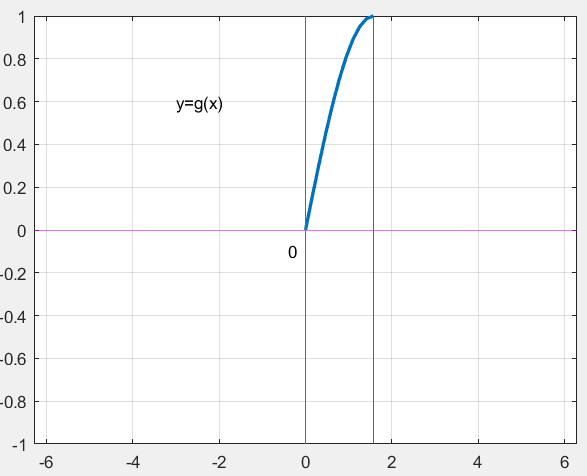
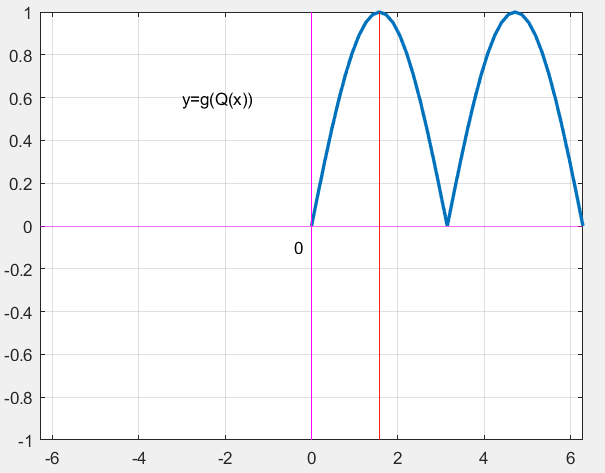
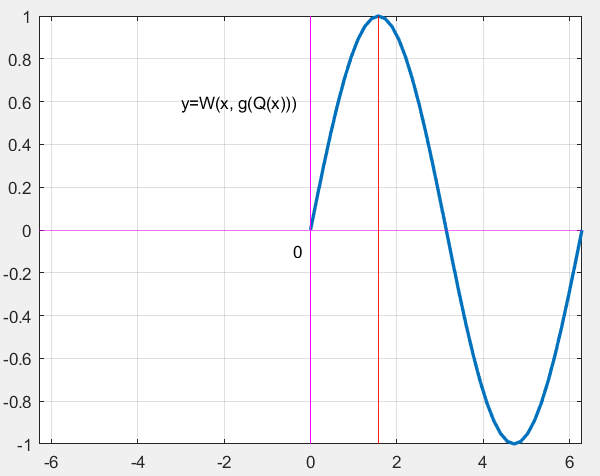
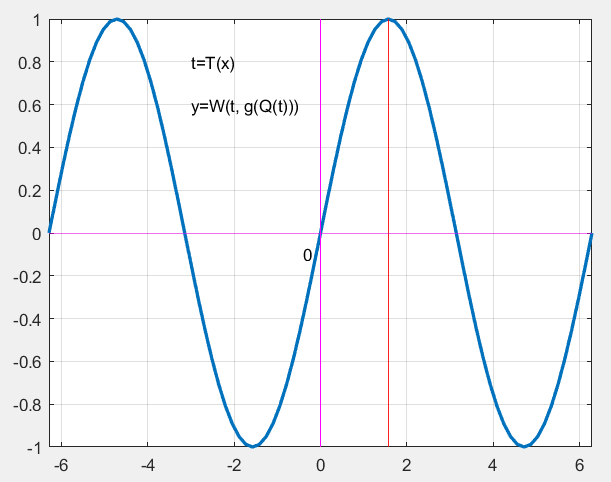
2. g(x)
算法的关键是通过g(x)来拟合f(x)在[0, π/2]的值。
g(x)的具体形式可以任意选择,例如选择CORDIC、泰勒展开、查表等等。g(x)是决定算法的精度与速度的核心因素。
以f(x) = sinx为例,取g(x)为泰勒4阶展开的结果:
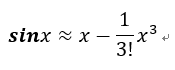
也可以取g(x)为泰勒6阶展开的结果:
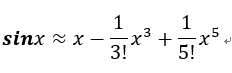
二. 误差评估模型
由于预处理机制的存在,我们只需讨论g(x)在[0,π/2]上对f(x)的拟合情况。为了便于数值分析,先将自变量x离散化:把X轴上的大区间[0,π/2]均分为 N=π/2ΔX 个区间,取每个区间的左端点代表整个区间,这样我们便在X轴上获得了 N 个点,每个点坐标为xi。记每个点处偏差为Di = g(xi) - f(xi) ,则标准偏差S表示为:
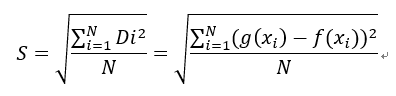
引入另一个量Dmax = max{ |Di| }表示峰值偏差。
这样,标准偏差S描述了g(x)的整体误差,而峰值偏差Dmax则描述了局部误差,综合这两个量即可对算法的误差进行评估。同时,上述方法与g(x)的具体形式无关,即无论采用何种拟合算法,该方法都适用。
仍以f(x) = sinx为例。令g(x) 为sinx的泰勒展开式。误差分析如下。
N = 10;泰勒展开阶数 = 4阶
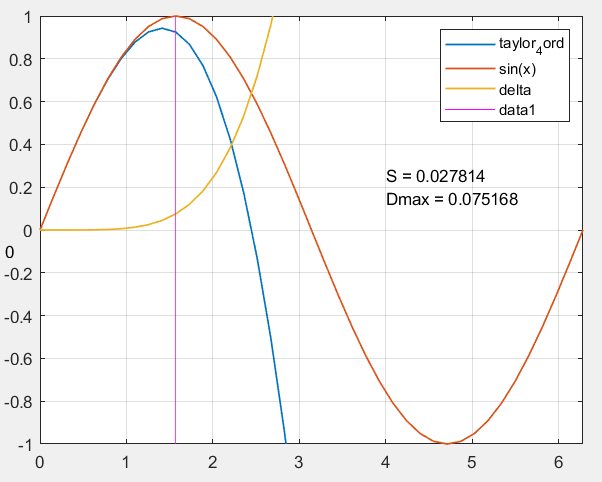
(注:紫线为x=π/2。只对区间[0,π/2]进行了误差统计,下同)
N = 10;泰勒展开阶数 = 6阶
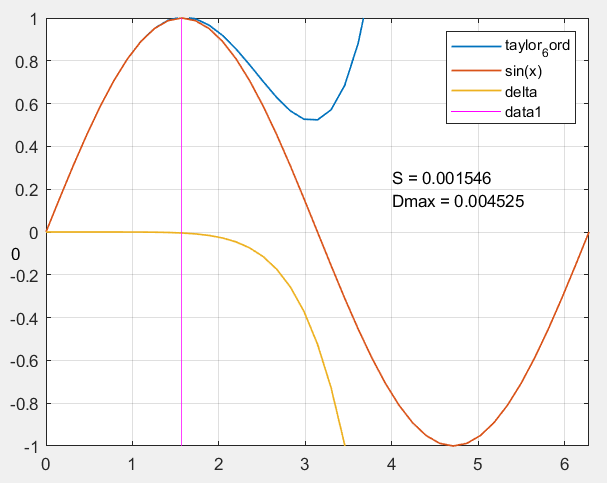
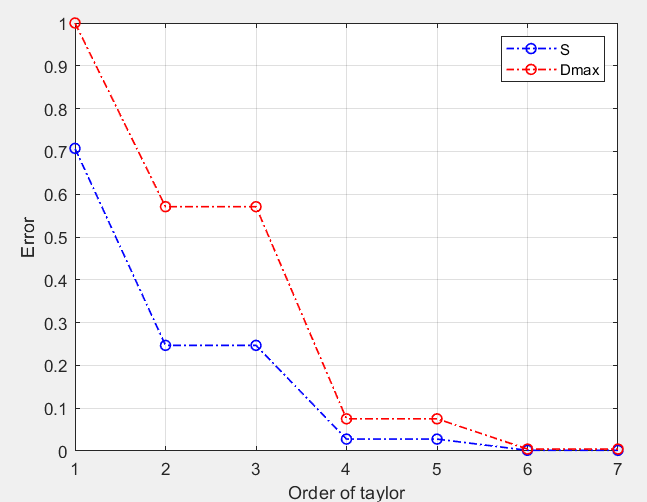
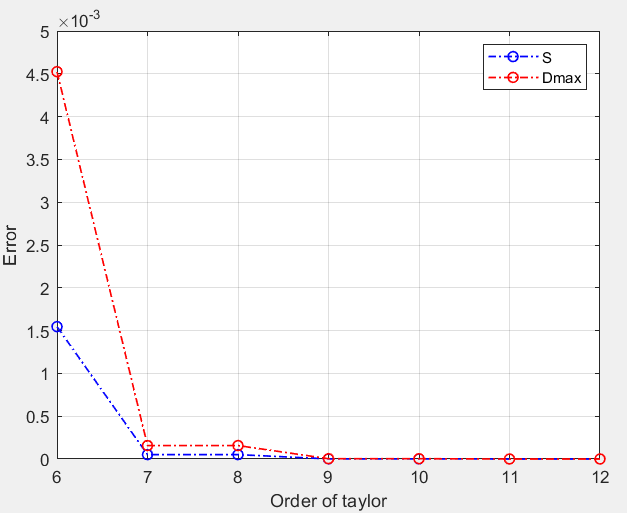
随着展开式阶数增加,标准偏差S和峰值偏差Dmax都呈近似指数减小,拟合精度增加。
三. 由误差导出设计
到此我们已经建立了评估误差的模型,但工作还远未完成。误差分析的最终目标是确定设计,之前的工作只实现了从设计求解误差;接下来的问题是如何已知误差,求解设计。
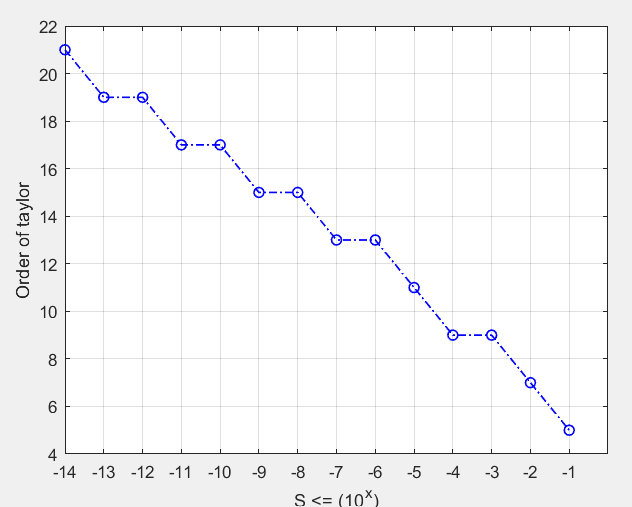
事实上,对于g(x)的某一形式而言,若误差模型的正向解法已经确定,那么通过枚举搜索的方式就可反向求解。算法的输入为最大允许标准偏差S或最大允许峰值偏差Dmax;算法对于每个给定的S或Dmax,通过n次迭代求出当前标准偏差或峰值偏差,当某次迭代得出的精度满足要求,那么此时n即为需要的阶数;输出n并结束。
利用上述算法绘制出“S的数量级--Taylor阶数”图。给定最大允许标准偏差,由图可得最小展开阶数。例如要求精度达到1e-14,至少应展开21阶。
实现绘图的Matlab代码如下:
1 n = 14;
2 expS = logspace(-n,-1, n);
3
4 ords = zeros(size(expS));
5 for i=1:size(expS, 2)
6 ords(i) = get_order(expS(i));
7 end
8
9 expSN = -n:-1;
10 plot(expSN,ords,'bo-.', 'LineWidth', 1);
11
12 grid on;
13 xlabel('S <= (10^x)');
14 ylabel('Order of taylor');
15 set(gca,'xtick',[-n:1:-1])
16
17 function v=taylor_n(x, n)
18 syms sx;
19 tayl = taylor(sin(sx), sx, 'Order', n);
20 v =eval(subs(tayl, sx, x));
21 end
22
23 function v=get_order(expS)
24 n = 1;
25 S = 2;
26 while S > expS
27 t=0:pi/20:pi/2;
28 delta = sin(t)-taylor_n(t, n);
29 S = sqrt(sum(delta.^2) / size(t,2));
30 Dmax = max(abs(delta));
31 n = n + 1;
32 end
33 v = n;
34 end
对于任意通过若干次迭代来逼近目标函数的算法,上述评估框架仍然适用,只需简单修改taylor_n函数的内容即可实现。
事实上,对于所有精度可变的算法,总存在一个可变因子n,当n增大时,算法精度增加,因此上述代码可修改为通用的框架:
1 n = 14; % 指定标准偏差S或峰值偏差Dmax的数量级范围[10^-1, 10^-n]
2 expS = logspace(-n,-1, n);
3
4 ords = zeros(size(expS));
5 for i=1:size(expS, 2)
6 ords(i) = get_order(expS(i));
7 end
8
9 expSN = -n:-1;
10 plot(expSN,ords,'bo-.', 'LineWidth', 1);
11
12 grid on;
13 xlabel('S <= (10^x)');
14 ylabel('Order of taylor');
15 set(gca,'xtick',[-n:1:-1])
16
17 %%
18 function v=fit_n(x, n)
19 % 在此处添加逼近算法的实现
20 end
21 %%
22
23 function v=get_order(expS)
24 n = 1;
25 S = 2; Dmax = 2;
26 while S > expS % 约束条件:可改为 Dmax > expDmax 来约束峰值偏差
27 t=0:pi/20:pi/2;
28 delta = sin(t)-fit_n(t, n);
29 S = sqrt(sum(delta.^2) / size(t,2));
30 Dmax = max(abs(delta));
31 n = n + 1;
32 end
33 v = n;
34 end
进一步地,若将多种不同的g(x)算法结合起来,综合考虑各种算法的资源占用、运行时间等因素,并编写程序完成筛选(例如优先选择精度高的算法,当精度相等时再优先选择效率高的算法),则设计过程就可以自动化。
相比于依赖设计者经验来筛选算法,分别对候选算法进行误差及资源评估,再通过对比做出最终决策的方法而言,本文所述的方法在一定程度上提高了工作效率。同时,由于误差评估模型不依赖于具体的算法实现,任意可行的算法都可以添加到框架中来,从而丰富框架的内容。