Python-圆周率的计算实例

1.近似公式计算

#CalPi.py
pi = 0;
N = 100;
for k in range(N):
    pi += 1/pow(16,k)*(4/(8*k+1)-2/(8*k+4)-1/(8*k+5)-1/(8*k+6));
print("圆周率的值是:{}".format(pi));

#运行结果
#圆周率的值是:3.141592653589793

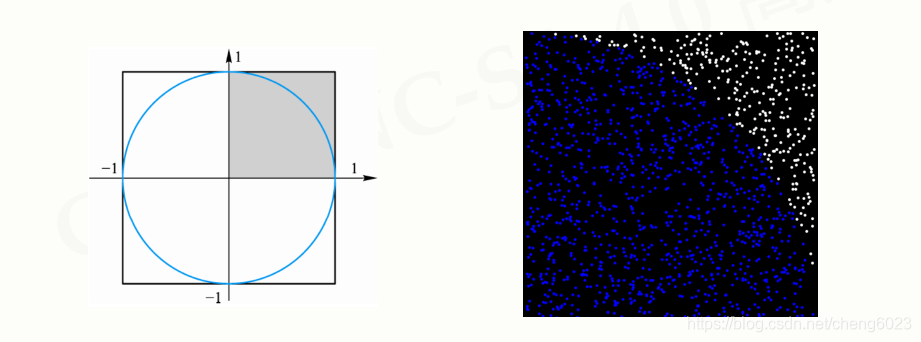
2.蒙特卡罗方法

蒙特·卡罗方法（Monte Carlo method），也称统计模拟方法，是二十世纪四十年代中期由于科学技术的发展和电子计算机的发明，而被提出的一种以概率统计理论为指导的一类非常重要的数值计算方法。是指使用随机数（或更常见的伪随机数）来解决很多计算问题的方法。与它对应的是确定性算法。蒙特·卡罗方法在金融工程学，宏观经济学，计算物理学（如粒子输运计算、量子热力学计算、空气动力学计算）等领域应用广泛。

数学应用：

通常蒙特·卡罗方法通过构造符合一定规则的随机数来解决数学上的各种问题。对于那些由于计算过于复杂而难以得到解析解或者根本没有解析解的问题，蒙特·卡罗方法是一种有效的求出数值解的方法。一般蒙特·卡罗方法在数学中最常见的应用就是蒙特·卡罗积分。

--百度百科

#CalPi.py
from random import random
from time import perf_counter

DARTS = 1000 * 1000;
hits = 0.0;
start  = perf_counter();
for i in range(1, DARTS+1):
    x,y = random(),random();
    dist = pow(x**2+y**2,0.5);
    if dist <= 1.0:
        hits += 1;
pi = 4 * (hits/DARTS);
print("圆周率的值是:{0}".format(pi));
print("运行时间是:{:5f}s".format(perf_counter()-start));

#运行结果
#圆周率的值是:3.142376
#运行时间是:0.746553s

3.举一反三：

数学思维：找到公式，利用公式求解

计算思维：抽象一种过程，用计算机自动化求解

 

本文仅为学习Python记录，部分素材来源于中国大学MOOC《Python语言设计》—嵩天

来源：CSDN

作者：cheng6023

链接：https://blog.csdn.net/cheng6023/article/details/101227688