
和P9.4思路一样,只是D=5,这里只放第1小题。
代码:
%% ------------------------------------------------------------------------
%% Output Info about this m-file
fprintf('\n***********************************************************\n');
fprintf(' <DSP using MATLAB> Problem 9.5.1 \n\n');
banner();
%% ------------------------------------------------------------------------
% ------------------------------------------------------------
% PART 1
% ------------------------------------------------------------
% Discrete time signal
n1_start = 0; n1_end = 100;
n1 = [n1_start:1:n1_end];
xn1 = cos(0.15*pi*n1); % digital signal
D = 5; % downsample by factor D
OFFSET = 0;
y = downsample(xn1, D, OFFSET);
ny = [n1_start:n1_end/D];
% ny = [n1_start:n1_end/D-1]; % OFFSET=2
figure('NumberTitle', 'off', 'Name', 'Problem 9.5.1 xn1 and y')
set(gcf,'Color','white');
subplot(2,1,1); stem(n1, xn1, 'b');
xlabel('n'); ylabel('x(n)');
title('xn1 original sequence'); grid on;
subplot(2,1,2); stem(ny, y, 'r');
xlabel('ny'); ylabel('y(n)');
title(sprintf('y sequence, downsample by D=%d offset=%d', D, OFFSET)); grid on;
% ----------------------------
% DTFT of xn1
% ----------------------------
M = 500;
[X1, w] = dtft1(xn1, n1, M);
magX1 = abs(X1); angX1 = angle(X1); realX1 = real(X1); imagX1 = imag(X1);
max(magX1)
%% --------------------------------------------------------------------
%% START X(w)'s mag ang real imag
%% --------------------------------------------------------------------
figure('NumberTitle', 'off', 'Name', 'Problem 9.5.1 X1 DTFT');
set(gcf,'Color','white');
subplot(2,1,1); plot(w/pi,magX1); grid on; %axis([-2, -1, -0.5, 0, 0.15, 0.5, 1, 2]);
title('Magnitude Response');
xlabel('digital frequency in \pi units'); ylabel('Magnitude |H|');
set(gca, 'xtick', [-2,-1.85,-1.5,-1,-0.15,0,0.15,0.5,1,1.5,1.85,2]);
subplot(2,1,2); plot(w/pi, angX1/pi); grid on; %axis([-1,1,-1.05,1.05]);
title('Phase Response');
xlabel('digital frequency in \pi units'); ylabel('Radians/\pi');
figure('NumberTitle', 'off', 'Name', 'Problem 9.5.1 X1 DTFT');
set(gcf,'Color','white');
subplot(2,1,1); plot(w/pi, realX1); grid on;
title('Real Part');
xlabel('digital frequency in \pi units'); ylabel('Real');
subplot(2,1,2); plot(w/pi, imagX1); grid on;
title('Imaginary Part');
xlabel('digital frequency in \pi units'); ylabel('Imaginary');
%% -------------------------------------------------------------------
%% END X's mag ang real imag
%% -------------------------------------------------------------------
% ----------------------------
% DTFT of y
% ----------------------------
M = 500;
[Y, w] = dtft1(y, ny, M);
magY_DTFT = abs(Y); angY_DTFT = angle(Y); realY_DTFT = real(Y); imagY_DTFT = imag(Y);
max(magY_DTFT)
ratio = max(magX1)/max(magY_DTFT)
%% --------------------------------------------------------------------
%% START Y(w)'s mag ang real imag
%% --------------------------------------------------------------------
figure('NumberTitle', 'off', 'Name', 'Problem 9.5.1 Y DTFT');
set(gcf,'Color','white');
subplot(2,1,1); plot(w/pi, magY_DTFT); grid on; %axis([-2,2, -1, 2]);
title('Magnitude Response');
xlabel('digital frequency in \pi units'); ylabel('Magnitude |H|');
set(gca, 'xtick', [-2,-1.5,-1,-0.5,0,0.5,0.75,1,1.25,1.5,2]);
subplot(2,1,2); plot(w/pi, angY_DTFT/pi); grid on; %axis([-1,1,-1.05,1.05]);
title('Phase Response');
xlabel('digital frequency in \pi units'); ylabel('Radians/\pi');
figure('NumberTitle', 'off', 'Name', 'Problem 9.5.1 Y DTFT');
set(gcf,'Color','white');
subplot(2,1,1); plot(w/pi, realY_DTFT); grid on;
title('Real Part');
xlabel('digital frequency in \pi units'); ylabel('Real');
subplot(2,1,2); plot(w/pi, imagY_DTFT); grid on;
title('Imaginary Part');
xlabel('digital frequency in \pi units'); ylabel('Imaginary');
%% -------------------------------------------------------------------
%% END Y's mag ang real imag
%% -------------------------------------------------------------------
figure('NumberTitle', 'off', 'Name', sprintf('Problem 9.5.1 X1 & Y--DTFT of x and y, D=%d offset=%d', D,OFFSET));
set(gcf,'Color','white');
subplot(2,1,1); plot(w/pi,magX1); grid on; %axis([-1,1,0,1.05]);
title('Magnitude Response');
xlabel('digital frequency in \pi units'); ylabel('Magnitude |H|');
set(gca, 'xtick', [-2,-1.85,-1.5,-1.25,-1,-0.75,-0.5,-0.15,0,0.15,0.5,0.75,1,1.25,1.5,1.85,2]);
set(gca, 'ytick', [-0.2, 0, 10, 20, 40, 51, 60]);
hold on;
plot(w/pi, magY_DTFT, 'r'); gtext('magY(\omega)', 'Color', 'r');
hold off;
subplot(2,1,2); plot(w/pi, angX1/pi); grid on; %axis([-1,1,-1.05,1.05]);
title('Phase Response');
xlabel('digital frequency in \pi units'); ylabel('Radians/\pi');
hold on;
plot(w/pi, angY_DTFT/pi, 'r'); gtext('AngY(\omega)', 'Color', 'r');
hold off;运行结果:
原始序列x[n],和按D=5抽取后的序列y[n]

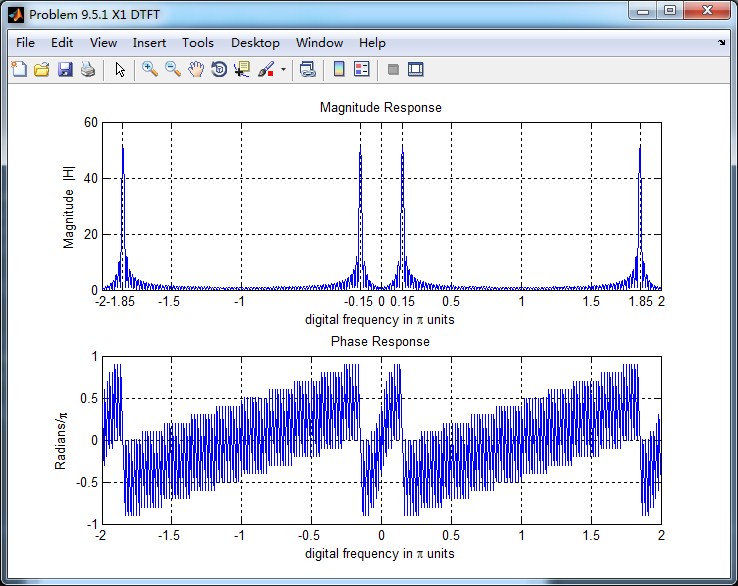
x[n]序列的DTFT
y[n]的DTFT
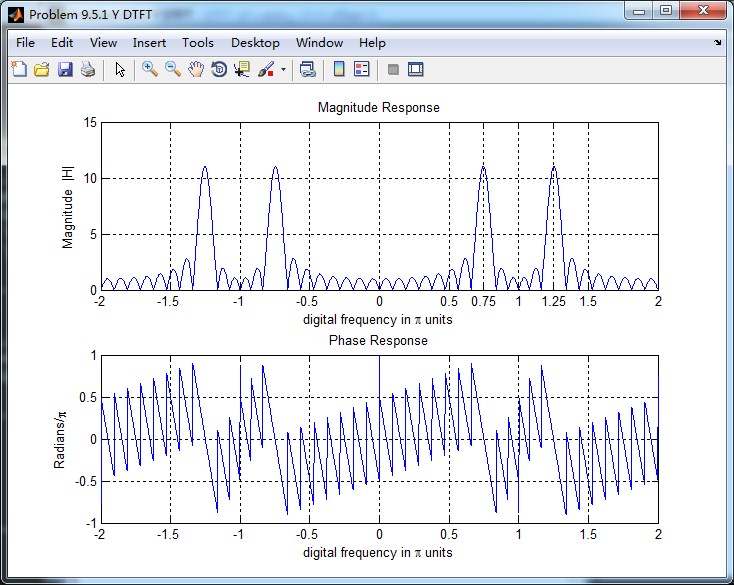
将二者叠合到一起,如下图,抽取后序列DTFT的幅度约为原始序列DTFT的五分之一(精确值为1/4.6248)。

其它小题这里不放图了。
来源:oschina
链接:https://my.oschina.net/u/4295884/blog/4334744