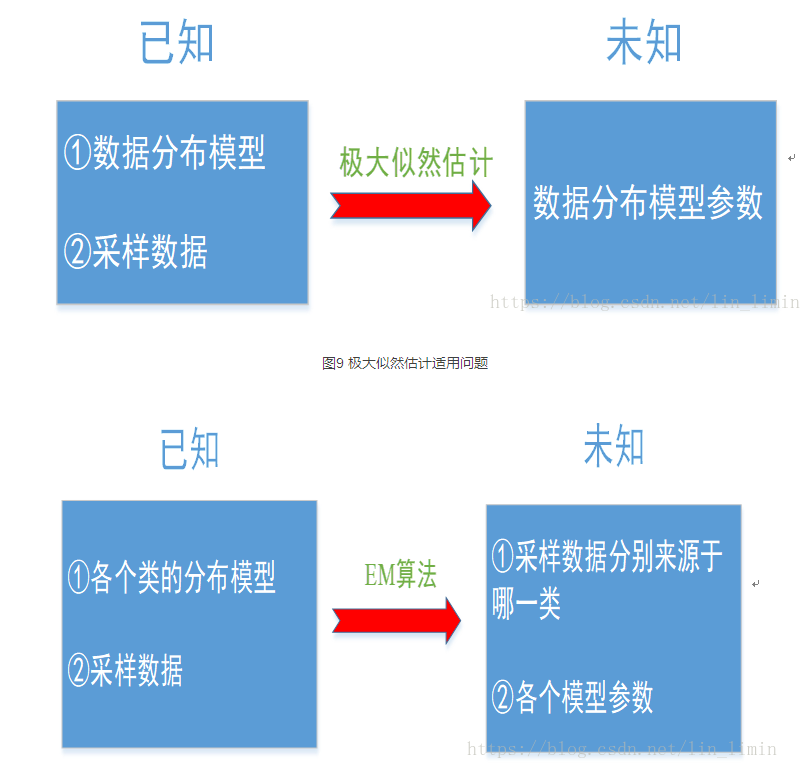
极大似然估计与EM算法:
详解EM算法与混合高斯模型(Gaussian mixture model, GMM)_林立民爱洗澡-CSDN博客 https://blog.csdn.net/lin_limin/article/details/81048411
GMM(高斯混合模型)以及简单实现_zjm750617105的专栏-CSDN博客 https://blog.csdn.net/zjm750617105/article/details/5243029
成分数的选择
在一个GMM里,BIC(Bayesian Information Criteria)准则是一种有效的成分数确定方法。注意,如果使用一个Variational Bayesian Gaussian mixture, 可以避免指定GMM的成分数。
AIC准则
AIC准则是由日本统计学家Akaike与1973年提出的,全称是最小化信息量准则(Akaike Information Criterion)。它是拟合精度和参数个数的加权函数: AIC=2(模型参数的个数)-2ln(模型的极大似然函数)
BIC准则
AIC为模型选择提供了有效的规则,但也有不足之处。当样本容量很大时,在AIC准则中拟合误差提供的信息就要受到样本容量的放大,而参数个数的惩罚因子却和样本容量没关系(一直是2),因此当样本容量很大时,使用AIC准则选择的模型不收敛与真实模型,它通常比真实模型所含的未知参数个数要多。BIC(Bayesian InformationCriterion)贝叶斯信息准则是Schwartz在1978年根据Bayes理论提出的判别准则,称为SBC准则(也称BIC),弥补了AIC的不足。SBC的定义为: BIC = ln(n)(模型中参数的个数) - 2ln(模型的极大似然函数值)
【sklearn第十九讲】高斯混合模型_python_wong2016的博客-CSDN博客 https://blog.csdn.net/wong2016/article/details/81057023
二维高斯分布(Two-dimensional Gaussian distribution)的参数分析_林立民爱洗澡-CSDN博客 https://blog.csdn.net/lin_limin/article/details/81024228
来源:https://www.cnblogs.com/wxl845235800/p/12178820.html