1.学习总结
1.1图的思维导图

1.2 图结构学习体会
深度优先遍历与广度优先遍历
- 不同点:广度优先搜索,适用于所有情况下的搜索,但是深度优先搜索不一定能适用于所有情况下的搜索。因为由于一个有解的问题树可能含有无穷分枝,深度优先搜索如果误入无穷分枝(即深度无限),则不可能找到目标节点。所以,深度优先搜索策略是不完备的
- 广度优先搜索适用范围:在未知树深度情况下,用这种算法很保险和安全。在树体系相对小不庞大的时候,广度优先也会更好些。
- 深度优先搜索适用范围:刚才说了深度优先搜索又自己的缺陷,但是并不代表深度优先搜索没有自己的价值。在树深度已知情况下,并且树体系相当庞大时,深度优先搜索往往会比广度优先搜索优秀,因为比如8*8的马踏棋盘中,如果用广度搜索,必须要记录所有节点的信息,这个存储量一般电脑是达不到的。然而如果用深度优先搜索的时候却能在一个棋盘被判定出来后释放之前的节点内存。
Prim和Kruscal算法
- Prim算法的实现过程:首先以一个结点作为最小生成树的初始结点,然后以迭代的方式找出最小生成树中各结点权重最小的边,并加到最小生成树中。(加入之后如果产生回路了就要跳过这条边,选择下一个结点。)当所有的结点都加入到最小生成树中后,就找出了这个连通图的最小生成树。
- Kruskal算法的实现过程:Kruskal算法在找最小生成树结点之前,需要对权重从小到大进行排序。将排序好的权重边依次加入到最小生成树中,(如果加入时产生回路就跳过这条边,加入下一条边)。当所有的结点都加入到最小生成树中后,就找到了这个连通图的最小生成树。
- Prim算法和Kruskal算法都是从连通图中找出最小生成树的经典算法。从策略上来说,Prim算法是直接查找,多次寻找邻边的权重最小值,而Kruskal是需要先对权重排序后查找的。
所以说,Kruskal在算法效率上是比Prim快的,因为Kruskal只需一次对权重的排序就能找到最小生成树,而Prim算法需要多次对邻边排序才能找到。
Dijkstra算法
- 迪杰斯特拉算法是从一个顶点到其余各顶点的最短路径算法,解决的是有向图中最短路径问题。迪杰斯特拉算法主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。(我觉得这个算法实质就是每一次你就在所有的路里面找一条最短的路走,这条路走完就不要再走了,在找一条,最后走到你要到的终点就行了,这个过程中没有任何的启发性,所以算法计算量就会很大,对于大型地图是不实际的,都得需要优化。
拓扑排序算法
- 对一个有向无环图进行拓扑排序,是将图中所有顶点排成一个线性序列,满足弧尾在弧头之前。这样的线性序列称拓扑序列。其实说白了,拓扑排序就是一个广度优先搜索。
拓扑排序的方法如下:
(1)从有向图中选择一个没有前驱(即入度为0)的顶点并且输出它.
(2)从网中删去该顶点,并且删去从该顶点发出的全部有向边.
(3)重复上述两步,直到剩余的网中不再存在没有前趋的顶点为止
2.PTA实验作业
题目1:7-1 图着色问题
1-1设计思路(伪代码或流程图)
bool flag = true;
bool vis[501];
int color[501] = {0};
int n,e,k;
MGraph g;
int main()
{
输入n,e,k为节点数、边数和颜色数
建图
输入 m
for(i=0 to i<m){
定义一个set容器s
for(j=0 to j<n){
输入颜色并保存在s
同时保存在color[j]
}
如果s里面的颜色数不等于k flag=false
否则{
将vis数组赋值为false
for(r=0 to r<n)
isYes(g,r);
如果flag==false break
}
}
如果flag==true 输出Yes
否则 输出No
}
void isYes(MGraph &g,int i) {
如果(vis[i]==false或者flag == false) 结束
令vis[i] = true;
for (int j = 0 to j < g.n) {
如果(color[i] == color[j] && g.edges[i][j] == 1) {
flag = false;
}
如果(g.edges[i][j] == 1 && vis[j] == false){
isYes(g,j);
}
}
}
1-2代码截图


1-3PTA提交列表说明

- 这题一开始的时候没有考虑图不连通的时候,导致部分正确,后来想用图的遍历来判断图是否连通,过程太复杂,还要多一个函数,而且有些判断可能会重复,所以后面就用过isYes函数里面通过vis和color进行判断,其实也是遍历,得到了正确答案
题目2:7-3 六度空间
2-1设计思路(伪代码或流程图)
主要函数
int BFS(AdjGraph *G,int v)
{
定义一个指针p
int queue[MAXV],front=0,rear=0,flag1,flag2;//queue为队列操作
int w,i,num=0,count=1;
visited[v]=1;
rear=(rear+1)%MAXV;
将v入队列
flag1=v保存v
while(front!=rear)
{
取队头元素w
p=G->adjlist[w].firstarc;
当p不等于NULL
如果 visited[p->adjvex]==0
visited[p->adjvex]=1;
令队尾元素等于p->adjvex
count++;
flag2保存p->adjvex
p指向下一条边
如果w等于flag1
num++;
flag1=flag2
当num等于6时 返回count
}
}
2-2代码截图
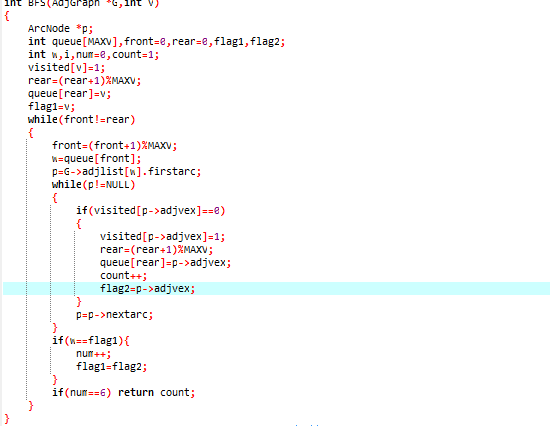

2-3PTA提交列表说明

- 这题其实就是对广度优先遍历的改造,多种错误是因为没有进行数量的判断,后面在进行遍历时,先用变量保存队列头结点,在进行一趟遍历后,如果尾节点跟头结点相同num++,这样就可以控制循环,当num到6时,就可以结束并返回值。
题目3:7-5 畅通工程之最低成本建设问题
3-1设计思路(伪代码或流程图)
主要函数
void Prim(int v)
{
令全局变量count=0
定义lowcost[1005]保存最短路径
将lowcost赋值为0
将节点v到各节点的距离保存在lowcost
for(i=1 to i<n){
min=INF;
找出lowcoat最小值min 保存下标于k
如果最小值不存在 输出Impossible
count+=min;
lowcost[k]=0;
for(j=1 to j<n){
如果g[k][j]!=0&&g[k][j]<lowcost[j]
lowcost[j]=g[k][j];
}
}
}
3-2代码截图

3-3PTA提交列表说明

- 一开始部分正确,最大N和M,还有不连通的情况过不了,解决不连通增加一个深度遍历来判断,但是最大N和M还是过不了,后来发现可以直接在prime函数里进行判断,如果min始终等于INF,就证明图不连通,改完后两个点都能过了。
3.截图本周题目集的PTA最后排名
3.1 PTA排名

- PTA总分为255在250分--310分之间
3.2 我的总分:2.5分
4. 阅读代码
地图建设问题
#include
#include
typedef char vextape[20];
typedef struct {
int avex,bvex;
float w;
}edge;
typedef struct{
int vexnum,edgenum;
edge mst[20];
vextape vexs[20];
float arcs[30][30];
}graphmatrix;
int locatevex(graphmatrix *g,vextape u){
int i;
for(i=0;ivexnum;i++){
if(strcmp(u,g->vexs[i])==0)
return i;
}
return 0;
}
void graphinit(graphmatrix *g){
int i,j,t;
float w;
vextape va,vb;
FILE *p;
p=fopen("graph.txt","r");
fscanf(p,"%d",&g->vexnum);
fscanf(p,"%d",&g->edgenum);
for(i=0;ivexnum;i++)
for(j=0;j<=i;j++)
{
g->arcs[i][j]=g->arcs[j][i]=32767;
}
for(i=0;ivexnum;i++){
fscanf(p,"%s",g->vexs[i]);
}
for(t=0;tedgenum;t++){
fscanf(p,"%s%s%f",va,vb,&w);
i=locatevex(g,va);
j=locatevex(g,vb);
g->arcs[i][j]=g->arcs[j][i]=w;
}
fclose(p);
}
void prim(graphmatrix *g){
int i,j,min;
int vx,vy;
float weight,minw;
edge e;
for(i=0;ivexnum-1;i++){
g->mst[i].avex=0;
g->mst[i].bvex=i+1;
g->mst[i].w=g->arcs[0][i+1];
}
for(i=0;ivexnum-1;i++){
minw=32767;
min=i;
for(j=i;jvexnum-1;j++){
if(g->mst[j].wmst[j].w;
min=j;
}
}
e=g->mst[min];
g->mst[min]=g->mst[i];
g->mst[i]=e;
vx=g->mst[i].bvex;
for(j=i+1;jvexnum-1;j++){
vy=g->mst[j].bvex;
weight=g->arcs[vx][vy];
if(weightmst[j].w){
g->mst[j].w=weight;
g->mst[j].avex=vx;
}
}
}
}
int main(){
int i;
float t=0;
graphmatrix gr;
graphinit(&gr);
prim(&gr);
printf("\n应该建设以下地铁线路:\n");
for(i=0;i %s, %.2f km\n",gr.vexs[gr.mst[i].avex],gr.vexs[gr.mst[i].bvex],gr.mst[i].w);
t+=gr.mst[i].w;
}
printf("\n总线路长为%f公里\n",t);
return 0;
}
- 此题是利用无向图最小生成树的方法使地铁到达各个区并且总的建设费用最小。利用图的经典算法解决实际应用问题(利用求最小生成树算法求解地铁建设最佳方案)。此题运用的图存储结构为邻接矩阵,只是对其进行了修改,定义一个结构体表示地铁建设的一些参数,在图的结构体中加入这些内容,之后就是对prime算法的运用和改造。
- 算法思想描述:
(1) 在输入图的顶点的过程中,我们给顶点安排的序号是以用户输入顶点的顺序为依据的。比如:用户输入的第一个顶点的序号默认为0,故该顶点的值存储在vexs[0]中……,当用户输完n个顶点后,这n个顶点就全部存储在数组vexs[0..n-1]中了。
(2) 图的输入:
步骤1:通过输入语句scanf接收用户输入顶点个数和边的条数:g->vexNum和g->edgeNum;
步骤2:给二维数组arcs赋初值使 g->arcs[1..vexNum-1][1..vexNum-1]=∞;
步骤3:通过输入语句scanf接收用户输入g->vexNum个顶点的值存放于一维数组g->vexs[0.. g->vexNum-1]中;
步骤4:通过输入语句scanf接收用户输入g->edgeNum条边的两个顶点的值及该边上的权值<va,vb,w> ;通过LocateVex查找va,vb在图中的序号i,j;然后执行:g->arcs[i,j]=g->arcs[j,i]= w ;
(3) 求图的最小生成树算法的实现
每求出最小生生的一条边的时候不是打印该边,而是将该边的两个顶点的序号存入指针变量pgraph (pgraph为指向存放图的GraphMatrix 类型变量的指针变量)所指的一维数组mst[0..n-2] 中(最小生成树只有n-1条边),即存入pgraph->mst[0..n-2] 中。
来源:https://www.cnblogs.com/mayifang/p/9192844.html