优雅的线性代数系列一



说道线性代数, 我们自然就想到矩阵, 那我们该如何理解矩阵呢?

矩阵与线性变换

若一个变换 \(L\) 满足以下两条性质

\[ \begin{align*} L(\vec v+ \vec w) &= L(\vec v) + L(\vec w) &(1) \text{"可加性"} \\ L(c\vec v) &= c L(\vec v) \quad\quad\ &(2) \text{"成比例"} \end{align*} \]

则称 \(L\) 是线性的.

值得注意的一点时, 线性变换中, 坐标系的原点不动, 即零向量的变换结果还是零向量.

我们来看看矩阵与线性变换的关系

\[ A(v+w) = Av + Aw \Leftrightarrow L(\vec v+ \vec w) = L(\vec v) + L(\vec w)\\ A(cv) = c(Av) \Leftrightarrow L(c\vec v) = c L(\vec v) \]

可以看出矩阵完全满足线性变换的要求, 所以现在你应该将矩阵看做线性变换, 这会给我们理解很多线性问题带来很大的好处.

\(\bigstar\) 如果想知道线性变换对于一个输入向量空间有什么影响, 我们只需要知道该线性变换对该输入空间的基有什么影响, 我们就能知道所有信息.

假设 n 维输入空间 \(R^n\) 的基为 \(v1, v_2, \dots,v_n\)

\[ \begin{eqnarray*} \forall \space v &=& c_1v_1 + c_2v_2 + \cdots + c_nv_n= [v_1,v_2,\cdots,v_n]\begin{bmatrix} c_1\\ c_2\\ \vdots \\c_n \end{bmatrix} \\ T(v) &=& c_1T(v_1) + c_2T(v_2) + \cdots + c_nT(v_n) \\ &=& c_1Av_1 + c_2Av_2 + \cdots + c_nAv_n \\ &=& [Av_1,Av_2,\cdots,Av_n]\begin{bmatrix} c_1\\ c_2\\ \vdots \\c_n \end{bmatrix} \end{eqnarray*} \]

其中 \(c =\begin{bmatrix} c_1\\ c_2\\ \vdots \\c_n \end{bmatrix}\) 即为 \(v\) 在该基下的坐标.

可以看出想知道向量 \(v\) 的线性变换结果, 我们只需要知道输入空间的基的变换结果, 然后乘以坐标就好.

下面复合线性变换的会给出例子直观的看看.

复合线性变换

我们可以通过线性变换具有顺序性的的角度理解下面 矩阵乘积 的性质

\[ A B \not= BA \\ ( A B) C = A ( B C) \]

\(\bigstar\) 矩阵的乘积 $ A B $ 可以看成是 复合线性变换. 复合线性变换可以看成两个线性变换有序叠加. 下面通过一个例子说明.

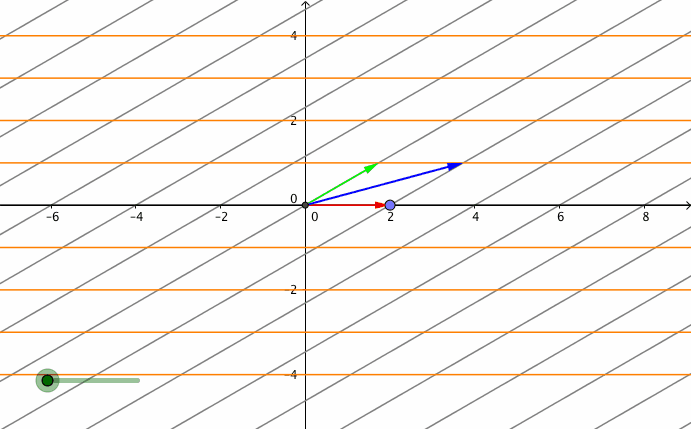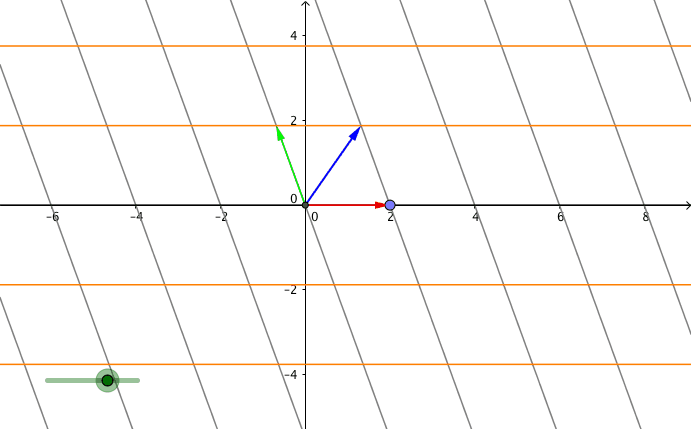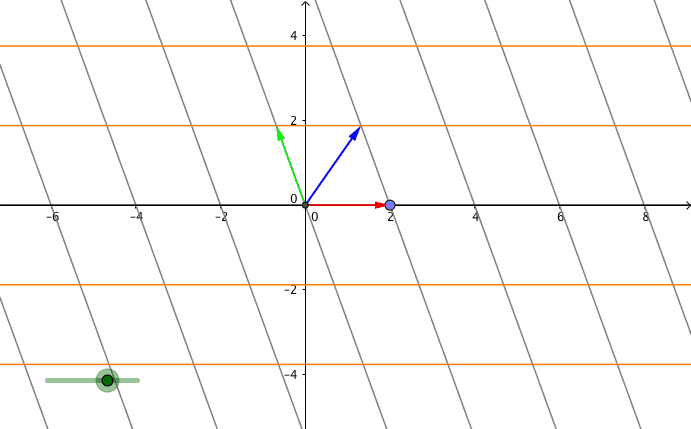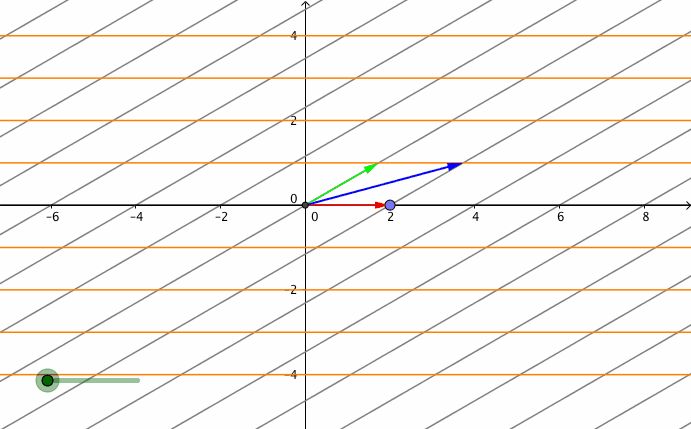
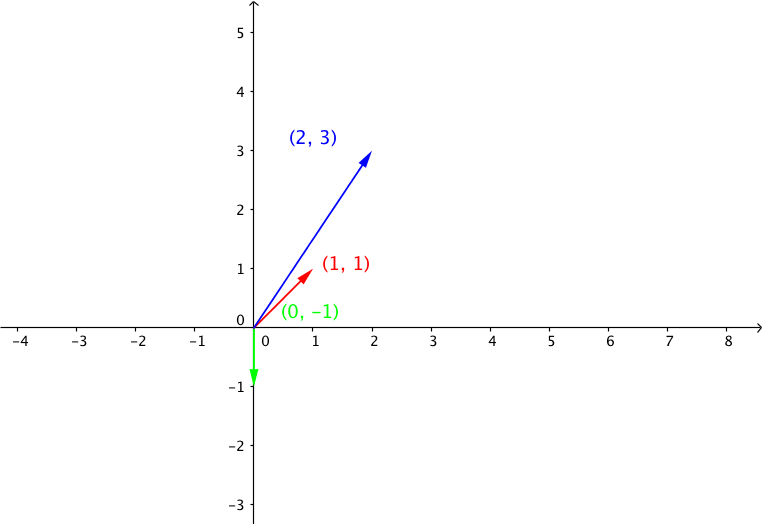
考虑 向量 $\vec v =[2, 3]^T $, 首先将该向量旋转 \(90^{\circ}\), 然后进行剪切变换.

\[ \begin{align*} A &= \begin{bmatrix} 1&1 \\ 0&1\end{bmatrix},B=\begin{bmatrix} 0&-1 \\ 1&0\end{bmatrix} \\ C &=AB=\begin{bmatrix} 1&-1 \\ 1&0\end{bmatrix} \end{align*} \]

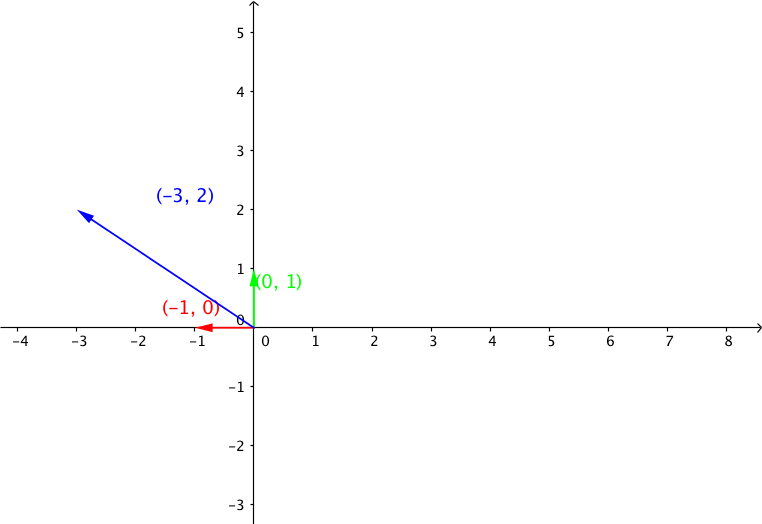
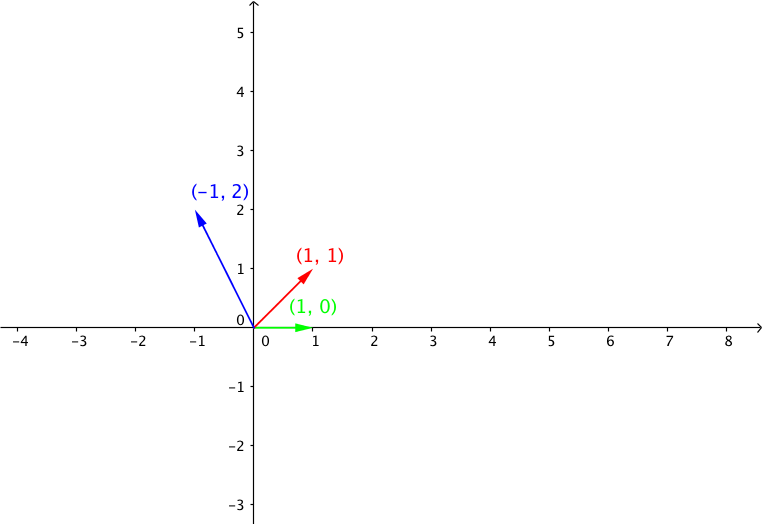
由于在二维标准正交坐标系中, 我们只要知道基向量的 \([0,1]^T, [1,0]^T\) 关于矩阵的变换结果, 乘以坐标就是变换结果. 由于由于这里是标准正交基, 所以基向量组成矩阵是单位矩 I, BI = B, 所以 矩阵 B 的列向量 就是基向量的经过线性变换 B 的变换结果.在下面的图中, 我们可以看到 基向量 以及 向量 \(v\) 经过矩阵 A, B线性变换之后的结果.

向量 $ v =[2, 3]^T $



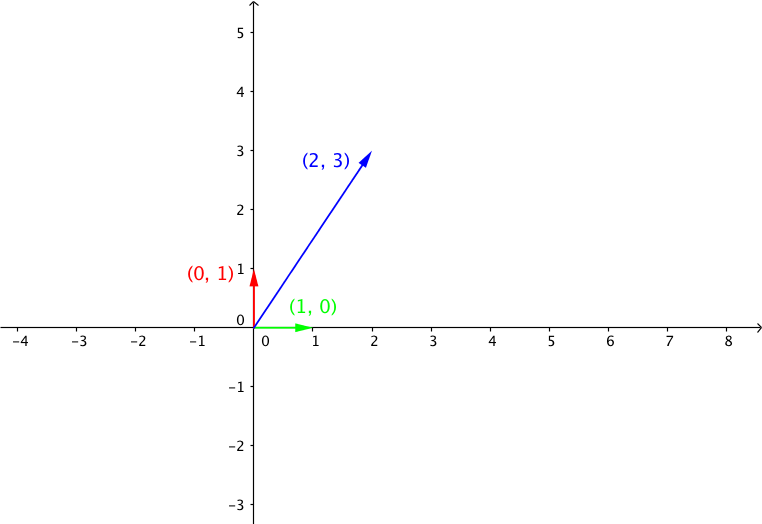
线性变换B: 向量 $ u = B v =[-3, 2]^T$, 其中 \(B=\begin{bmatrix} 0&-1 \\ 1&0\end{bmatrix}\)



线性变换A: 向量 $ w = Au = [-1,2]^T$, 其中 \(A = \begin{bmatrix} 1&1 \\ 0&1\end{bmatrix}\)



我们可以看出基向量的线性变换结果就是矩阵 A, B 的对应的列向量.

我们再来看看复合线性变换C 的线性变换

复合线性变换 C, 向量 \(p = Cv\), 其中 \(C=\begin{bmatrix} 1&-1 \\ 1&0\end{bmatrix}\)



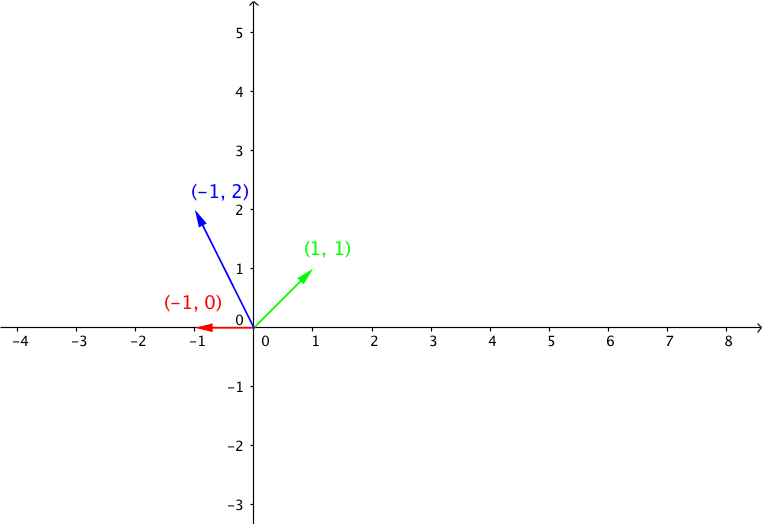
向量\(v\) 变换结果 \(w = p\), 希望现在你已经形成了以线性变换的角度思考矩阵乘法的思考方式.

逆矩阵和逆变换

\(b= Ax\) 表明矩阵 A 将向量 x 线性映射到 向量 b, 那如何将向量 b 变回到之前的向量 x 呢? 我们只需要进行逆变换就好了, 而逆变换对应的矩阵就是逆矩阵.

\[ \begin{align*} b &= A x \\ \quad x &= A^{-1} b, \space if \space \exists A^{-1} \end{align*} \]

\(|A| \not= {0}\) 矩阵的行列式不为零表示线性变换不会将高维映射到低维, 即不会损失信息, 所以可以通过逆变换得到变换之前的向量.

还是 复合线性变换的例子 其中

\[ \begin{align*} 变换前向量 \quad v &= [2, 3]^T \\ 变换后向量 \quad w &= [-1,2]^T \\ C &= \begin{bmatrix} 1&-1 \\ 1&0\end{bmatrix} \\ C^{-1} &= \begin{bmatrix} 0&1 \\ -1&1\end{bmatrix} \\ w &=Cv \\ v & = C^{-1}w \end{align*} \]



可逆矩阵的定义为
\[ AA^{-1}=I \\ A^{-1}A=I \]

求逆运算 \(Gussian{\rm -}Jordan\) 消元法

\[ \begin{align*} & \space E\left[ A \space\vdots \space I \right] = [I: E] \quad 増广矩阵\\ &\because EA = I\\ &\therefore E = A^{-1} \end{align*} \]

\(🎵\) 非奇异矩阵杂谈

可逆矩阵又称为非奇异矩阵, 不可逆矩阵称为奇异矩阵

Q: “奇异”一词通常指奇特的，为什么称可逆矩阵为“非奇异” ？它们有什么奇异之处？

A: 数学上， “奇异”（singular）一词用来形容破坏了某种优良性质的数学对象。
对于矩阵来说， “可逆”是一个好的性质， 不可逆的矩阵就称为“奇异”矩阵。 比如矩阵的不可逆，等价于行列式为零或非满秩，等价于某个线性变换退化. 所有的矩阵都可看作线性变换. 这个奇异性就很好理解了， 变换完丢失了东西的情况都是不好的， 也就是奇异的。

行列式的几何意义

二维坐标中, 线性变换 \(\vec A\) 的行列式 \(|A|\) 的绝对值 \(\lambda\) 表示变换后区域的面积是变换前的 \(\lambda\) 倍; 如果行列式的值 \(det \vec A\)为负数表示这样的变换改变了空间的定向. 在三维空间中, 线性变换 \(\vec A\) 的行列式 \(|A|\) 的值可以理解为体积的变化.

初等变换

初等矩阵左乘矩阵 \(\longrightarrow\) 行变换

\(row_2 - 3 row_1\)
\[ \begin{bmatrix} 1 & 0 & 0 \\ -3 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} 1 & 2 & 1 \\ 3 & 8 & 1 \\ 0 & 4 & 1 \end{bmatrix}=\begin{bmatrix} 1 & 2 & 1 \\ 0 & 2 & -2 \\ 0 & 4 & 1 \end{bmatrix} \]

初等矩阵右乘矩阵 \(\longrightarrow\) 列变换

\[ \begin{bmatrix} 1 & 2 & 1 \\ 3 & 8 & 1 \\ 0 & 4 & 1 \end{bmatrix}\begin{bmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix}=\begin{bmatrix} 2 & 1 & 1 \\ 8 & 3 & 1 \\ 4 & 0 & 1 \end{bmatrix} \]

向量空间

n维向量空间 \(\mathbb R^n\)

给定域F，F 上的向量空间 V 是一个集合，其上定义了两种二元运算：

1. 向量加法： 把 V 中的两个元素u和v映射到V中另一个元素，记作 u + v；
2. 标量乘法： 把 F 中的一个元素 a 和 V 中的一个元素 u 变为 V 中的另一个元素，记作 a ·u。

\(\bigstar\) 零向量一定在向量空间

向量子空间

线性代数中子空间的定义

设W为数域F上的n维线性空间V的子集合（即W∈V），若W中的元素满足
（1）若任意的α，β∈W，则α+β∈W；（对加法是封闭的）
（2）若任意的α∈W，λ∈F，则λα∈W。（对数乘也是封闭的）
（3）子空间中必须包含“0向量”
则容易证明：W也构成数域F上的线性空间。称W是线性空间V的一个线性子空间，简称子空间。

比如说 3维向量空间 \(R^3\) 的子空间

1. \(R^3\)
2. 可以是一条过原点(0,0,0)的平面;
3. 可以是一条过原点(0,0,0)的直线;
4. 零向量空间(只包含零向量)

\[ A = \begin{bmatrix} 1&3\\2&3\\4&1\end{bmatrix} \]

如果 U, V 是向量空间 P 的子空间, 那么 \(S = U\cap V\)也是 P 的子空间
\[ \forall a, b \in S \because S = U\cap V, \therefore a, b \in U , V \]
在 \(U, V\) 中, \(a, b\) 符合加法封闭性和乘法封闭性, 即 \(a, b\) 的张成的向量空间同时在 \(U 和 V\) 中, 所以 \(a, b\) 的张成的向量空间在 \(S\) 中, 即 \(S\) 空间中符合加法封闭性和乘法封闭性, 所以 \(S\) 也是 \(P\) 的子空间.

正交子空间

\(\square\) 向量子空间正交

① 若内积空间中两向量的内积为0，则它们正交。

② 若内积空间中的向量 \(v\) 与子空间A中的每个向量都正交，那么这个向量和子空间 A 正交。

③ 若内积空间的子空间 A 和 B 满足一者中的每个向量都与另一者正交，那么它们互为正交子空间。

(正交子空间只有一个交点, 即零点)

矩阵空间

矩阵是一种特殊的向量的空间, 满足加法封闭性和数乘封闭性
比如说全部 \(R^{n \times n}\) 矩阵组成的矩阵空间(matrix space), 满足加法封闭性和数乘封闭性
其子空间包括 三角矩阵, 对称矩阵, 对角矩阵

那么矩阵空间 \(M\) 的基是什么?

就 3 维矩阵空间而言, 维度 dim = 9, 基为

\[ \underbrace{\begin{bmatrix} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}\begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}\begin{bmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}{\huge \dots} \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix}}_{9个} \]

3维对称矩阵空间 U 的维度为 dim = 6
3维三角矩阵空间 V 的维度为 dim = 6
3维对角矩阵空间 S 的维度为 dim = 3, \(S = U \cap V\)

\(U \cup V\) 不是向量空间.所以不考虑; \(U + V\)表示向量空间 U, V 的基向量张成的空间, 这里 \(U + V\)就是3维矩阵空间(二者的基组合可以得到3维矩阵空间的基), 维度为 9.

介绍另一个向量空间,

\[ \frac{d^2y}{dx^2} +y=0 \\ \Rightarrow y = c_1\sin x + c_2 \cos x, \forall c_1, c_2 \in R \]

这里 \(\sin x, \cos x\) 是二街常微分方程解空间的基向量, 虽然 \(\sin x, \cos x\) 并不那么像向量, 而是函数. 我们可以看到线性代数的知识的应用.

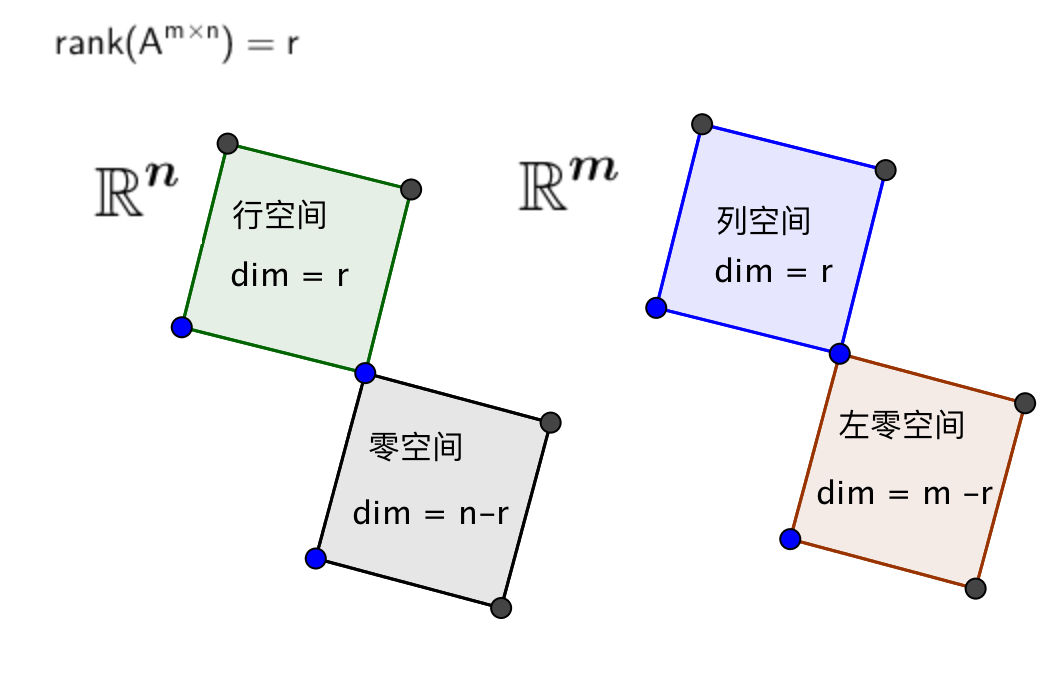
四个基本子空间

 

\(\blacksquare\) 矩阵 \(A^{m \times n}\) 的行空间和零空间正交, 行空间和零空间是将整个 n 维空间一分为二的两个相互正交的子空间; 称为 n 维空间的正交补, 即零空间包含所有正交于行空间的向量.

\(bigstar\) 正交补并不意味着二者并集等于整个 n 维空间, 比如二维空间中垂直的两条直线, 互为正交补, 却二者并集只是二维空间的一小部分而已.

零空间是方程 \(Ax=0\) 解

\[ \begin{gather*} Ax = \begin{bmatrix} a_1^T \\ a_2^T \\ \vdots \\ a_m^T \end{bmatrix}x = \begin{bmatrix} a_1^T x \\ a_2^T x \\ \vdots \\ a_m^T x \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ \vdots \\ 0 \end{bmatrix}, x \in N(A) \end{gather*} \]

所以矩阵 A 的行空间和 A 的零空间正交.



 

矩阵乘以列向量是矩阵列的线性组合, 结果为列向量;
行向量乘以矩阵是矩阵行的线性组合, 结果为行向量.

下面可一个简单的 矩阵乘以列向量 的例子

\[ \begin{bmatrix} \color{red}a &b \\ \color{red}c& d \end{bmatrix} \begin{bmatrix} x\\y \end{bmatrix} =\underbrace{ x \begin{bmatrix}\color{red}{ a\\ c} \end{bmatrix} + y\begin{bmatrix} b\\ d \end{bmatrix} }_{直观的部分在这里} \]

矩阵\(A^{m\times n}\)的四个基本子空间

① 列空间 column space \(C(A) \subset R^m, R^m的子空间\)
② 行空间 row space \(C(A^T) \subset R^n\)
③ 零空间 null space \(N(A) \subset R^n\)
④ 左零空间 null space of \(A^T\) \(N(A^T) \subset R^m\)

矩阵\(A^{m\times n}\)的行空间和列空间具有相同的秩 rank(A)

类型	表示	向量父空间	维度
列子空间	C(A)	\(R^m\)	rank(A)
行子空间	C(\(A^T\))	\(R^n\)	rank(A)
零子空间	N(A)	\(R^n\)	n - rank(A)
左零子空间	N(\(A^T\))	\(R^m\)	m - rank(A)

其中,

\[ dim(C(A)) + dim(N(A^T)) = m \\ dim(C(A^T)) + dim(N(A)) = n \\ \]

初等行变换(左乘)不会改变行空间, 但会改变列空间, 行变换只是对行进行了线性组合
初等列变换(右乘)不会改变列空间, 但会改变行空间, 列变换只是对列进行了线性组合

\[ A=\begin{bmatrix} 1 & 2 & 3 & 1 \\ 1 & 1 & 2 & 1 \\ 1 & 2 & 3 & 1 \end{bmatrix}\underrightarrow { 行变换} \begin{bmatrix} 1 & 0 & 1 & 1 \\ 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix}=R \]

显然, 列空间 \(C(A)\not= C(R)\), 行空间 \(C(A^T) = C(R^T)\)



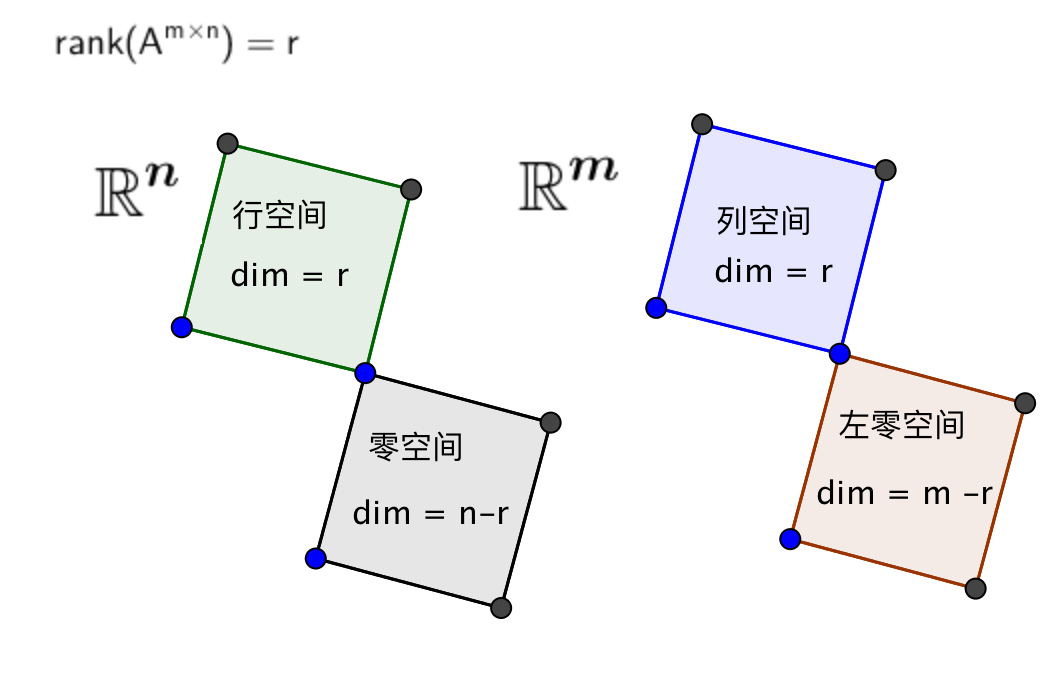
为什么\(N(A^T)\)叫做左零空间?

方程
\[ A^T \bf x=0 \]
方程的解 \(x\) 在 A 的零空间 \(N(A)\) 里

\[ A^T \bf y=0 \\ (A^T y)^T = 0^T \\ \Rightarrow y^T A = O^T \]

方程的解 \(y\) 在矩阵 \(A\) 的左边, 这就是为什么 \(N(A^T)\) 称为在矩阵 A 的左零空间.

列空间

矩阵 A 的列向量的所有线性组合构成了 \(R^3\) 的子空间, 称之为列空间.
方程
\[ Ax = b \]
有解, 当且仅当 b 在 A 的列空间中.

零空间

方程

\[ A \bf x = \bf 0 \]

的解, 又称之为零空间. 能称之为向量空间的原因就是

\[ A \bf x =\bf 0 \\ A \bf {x^*} = \bf 0 \\ \Rightarrow A (\bf x + \bf {x^*}) = A \bf x + A \bf {x^*} = \bf 0 \\ A (\bf\lambda x) = \lambda A\bf x = \bf 0 \\ \]
满足加法封闭性和数乘封闭性.

比如
\[ \begin{bmatrix} 1 & 1 & 2 \\ 2 & 1 & 3 \\ 3 & 1 & 4 \\ 4 & 1 & 5 \end{bmatrix}\begin{bmatrix} x_{ 1 } \\ x_{ 2 } \\ x_{ 3 } \end{bmatrix}=\begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \end{bmatrix} \]

方程 \(A \bf x= \bf 0\)的解(零)空间为 \(\quad \bf x = c\begin{bmatrix} 1 \\ 1 \\ - 1 \end{bmatrix},\quad \forall c \in R\).

除了 \(\bf b\) 是零向量, 方程 \(Ax = b\) 的解不构成向量空间(显然零向量不在解中)

四个子空间的基

列空间, 我们将其化为最简行阶梯型矩阵, 列空间的维数等于rank(A) = 行阶梯型矩阵的主元个数 = 基向量的个数,

我们找 rank(A) 个线性无关的列作为基向量即可.

列空间的维数等于行空间的维数, 所以我们找 rank(A) 个线性无关的行向量作为基, 就能求出行空间的基.

方程 \(A\bf x=0\) 的零空间之前求过. 我们可以在求零空间的同时求出左零空间, 不过我们需要多做一点工作.

回顾求逆运算 \(Gussian\)-\(Jordan\) 消元法

\[ \begin{align*} & \space E\left[ A \space\vdots \space I \right] = [I: E] \quad 増广矩阵\\ &\because EA = I\\ &\therefore E = A^{-1} \end{align*} \]

虽然这里我们的 A 并不一定是方阵, 不过我们依然可以使用 \(Gussian\)-\(Jordan\) 消元法记录行变换的过程.

\[ \begin{align*} & \space E\left[ A \space\vdots \space I \right] = [R: E] \\ \end{align*} \]

\(R\) 为行阶梯型矩阵, \([R: E]\) 中记录了矩阵 \(A \rightarrow R\) 的变换过程.

\[ \begin{eqnarray*} [A \vdots I] &=&\left[ \begin{matrix} 1 & 2 & 2 & 2 {\space \large \mid\space} 1&0&0\\ 2 & 4 & 6 & 7{\space \large \mid\space} 0&1&0 \\ 3 & 6 & 8 & 9 {\space \large \mid\space} 0&0&1\end{matrix} \right] \\ \Downarrow \\ [R\vdots E] &=& \begin{bmatrix} 1 & 2 & 2 & 2 {\space \large \mid\space} \quad \space 1&0&0 \\ 0 & 0 & 2 & 3 {\space \large \mid\space}-2&1&0 \\ 0 & 0 & 0 & 0 {\space \large \mid\space}-1&-1&1\end{bmatrix} \\ \end{eqnarray*} \]

矩阵 \(R\) 最后一行为 0, 是变换矩阵 \(E\) 最后一行向量与矩阵 A 乘积的结果, \(y^TA = 0^T\), 所以该行向量是左零空间的基向量. R 矩阵一共有 m - rank(A) 个零行. 故左零空间的维数是 m - rank(A). 上述矩阵秩为2, 所以左零空间维数为 \(3 - 2 = 1\), 矩阵 A 的 左零空间 为:

\[ \bf y = c\begin{bmatrix} -1\\-1\\1\end{bmatrix}, \forall c\in R \]

线性相关性

\(\square\) 给定向量组 \(A: a_1, a_2,\cdots,a_m\)存在不全为零的数 \(k_1, k_2,\cdots, k_m,\) 使得
\[ k_1a_1+k_2a_2+\cdots+k_ma_m = 0 \]
则称向量组 A 是线性相关的, 否则称它为线性无关.

\(\square\) 矢量空间的一组元素中，若没有矢量可用有限个其他矢量的线性组合所表示，则称为线性无关或线性独立(linearly independent)，反之称为线性相关(linearly dependent)

\(\square\)\(m 个 n 维向量组, \space 当维数小于向量个数时, 一定线性相关\)

\(\square\) 向量组 \(A: a_1, a_2,\cdots,a_m\)线性无关, 向量组 \(A: a_1, a_2,\cdots,a_m, a_{m+1}\)线性相关, 则向量 b 必能由向量组 A 线性表示, 且表示式惟一.

\(square\) 空间 \(S\)由向量组 \(A: a_1, a_2,\cdots,a_m\) 所张成, 那么空间 \(S\) 包含向量组所有的线性组合. 这里并不要求向量组 A 是线性无关的.

\[\downarrow\]

\(\square\) 说向量组 \(A: a_1, a_2,\cdots,a_n\)是空间 \(S\) 的基, 则向量组 A 具有如下特征

\[ \begin{gather} &向量组 A& \quad {线性无关} \tag {9.1} \\ &向量组 A& \quad 张成向量空间 S \tag{9.2} \end{gather} \]
且向量空间 \(R^n\) 基向量的个数等于 \(n\), 即空间的维数.

齐次方程组的解

\(\square\) 齐次方程组 \(Ax=0\) 的解由矩阵 A 的列向量的线性相关性决定. A 的列向量的线性相关, 方程有无穷解; A 的列向量的线性无关, 方程只有零解.

消元法求解齐次方程组

\[ \begin{eqnarray*} A = \begin{bmatrix} 1 & 2 & 2 & 2 \\ 2 & 4 & 6 & 8 \\ 3 & 6 & 8 & 10 \end{bmatrix} \\ \rightarrow \begin{bmatrix} 1 & 2 & 2 & 2 \\ 0 & 0 & 2 & 4 \\ 0 & 0 & 0 & 0 \end{bmatrix} \\ \rightarrow \begin{bmatrix} 1 & 2 & 0 & -2 \\ 0 & 0 & 1 & 2 \\ 0 & 0 & 0 & 0 \end{bmatrix} \\ \end{eqnarray*} \]

对于矩阵 \(A_{m\times n}\), 把行最简型中 r 个非零行的非零首元对应的未知数作为主元, 其余 n - r 个元素作为自由变量

\[ \begin{cases} \begin{align*} x_1 + 2x_2 \quad\quad - 2x_4 &= 0 \\ \quad \quad \quad x_3+2x_4 &= 0 \end{align*} \end{cases} \]

\((x_3,x4 {取任意值}), 令 x2 = c1, x4 = c2, c1,c2 \in R\), 则
\[ \begin{cases} \begin{eqnarray*} x_1 &=& -2c1 + 2c2 \\ x_2 &=& \quad \space \space c1 \\ x_3 &=& \quad\quad \space-2c2 \\ x_4 &=& \quad\quad \quad\quad c2 \end{eqnarray*} \end{cases} \]

所以 \(A\bf x = bf 0\) 的解(零)空间为

\[ \bf x = c1[-2, 1, 0,0]^T + c2[2,0,-2,1]^T \]

来源：https://www.cnblogs.com/nowgood/p/linearalgebra01.html