没有用的话qaq :
Ummmm...图论的大部分知识本来早就有学过,只是一直没有写成博文来梳理,但既然上了qbxt DP图论就写一篇来总结下,主要是来听DP的,但...由于太菜的原因,DP听得天花乱坠QWQ **
一,图:图是边和点组成的几何体 G=< V , E > V是点集合,E是边集
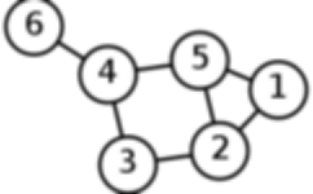
形如这样的东西就是一个图
二,图的相关基本概念
1,边:图上连接点和点之间的东西叫做边,图上边分为有向边和无向边。有向边是有方向的边,无向边是没有方向的边,在图上具体体现为有无箭头。
2,点:图上的点
3,权:就是某个东西的大小,图中一般会存在点权和边权,就是给点赋一个值和给边赋一个值,没有权的情况称为无权,权值为负的时候称为负权(注意以后算法中的负权边)
4,环:无向边中的环就像上图中的1,2,5和2,3,4,5,环的特点是,环上任意一点能到达通过环能回到自己!!有向图的环相同,就是一个点如果能通过一条路径回到自己,我们就说这条路径是一个环,负环的定义为环上所有边权之和小于零。
5,重边:即两个点之间有重复的边,但注意两个点之间重复但方向不同的边不属于重边。
6,有向无环图(DAG):字面意思,是有向图且没有环的图称为有向无环图,简称DAG,一般与有向图缩点后拓扑排序后,DAG上的DP有关,同时DP的实质是个DAG。
7,路径:从一条边到另一条边的路称为路径,简单路径是一条没有环的路径。
8,连通:如果一个点A能到达另一个点B,称为点A和点B连通,如果点B也能到达A点则称点A和点B是强连通的,从图中某一点出发,如果能到达图上任意一点,则称,这个图是一个连通图。
三,特殊的图
1,树:树是一种特殊的图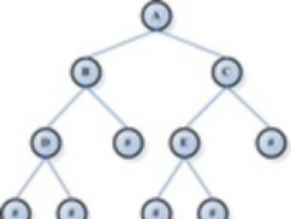
2,完全图:图上任意两点之间都有一条无向边的图
3,竞赛图:与完全图长得完全一致,不过竞赛图上的边有方向
4,基环树:有一个环,这个环向四周发散的全是树,这种图叫做基环树。
5,仙人掌图:每条边至多在一个环上的图
四,图的存储方式
图的存储存的都是有向边,对于无向边的情况,我们将其拆成两条有向边存储。
1,邻接矩阵
邻接矩阵因为比较耗内存O( n^2 ),且遍历较慢的原因,在OI中并不常用,因为博主比较弱,博主认为只有floyd会用的这个怪怪的东西。
邻接矩阵就是一个二维数组,二维数组就是矩阵嘛,一开始我们要对邻接矩阵进行初始化,可能置成0,可能置成-1,也可能置成正无穷,无论置成什么,都代表没有边(即如果 g[a][b]=初始化的值则代表a到b之间没有边)。
加边的话也很简单,就是如果是s到e存在一条边权为d的边,那么g[s][e]=d,同时要注意某些题目有重边的情况,以防需要留下的边权被不需要留下的冲刷掉,一般我们会留下边权最小的边或者边权最大的边,留下的方法就是加个if判断一下。
邻接矩阵的有点是可以快速知道s到e之间有没有边,边权是多少,缺点是遍历时间复杂度较高,同时,定义较浪费空间(因为有很多节点之间没有边)。
2,邻接表
比起邻接矩阵,邻接表是OI中最常用的存图方法
其原理是用了n个链表,用一个first数组在存边的时候将从某节点出发的所有边串了起来。
struct node
{
int ed,len,nxt;
};
node edge[2333];
int first[2333],cnt;
inline void add_edge(int s,int e,int d)
{
cnt++;
edge[cnt].ed=e;
edge[cnt].len=d;
edge[cnt].nxt=first[s];
first[s]=cnt;
return;
}//加边
int main()
{
scanf("%d%d%d",&s,&e,&d);
add_edge(s,e,d);
//add_edge(e,s,d); 若是无向边
}
for(int i=first[s];i;i=edge[i].ed)
{
}//遍历从s出发的所有边
写在最后 Yousiki Orz