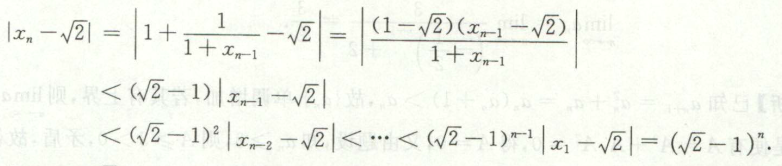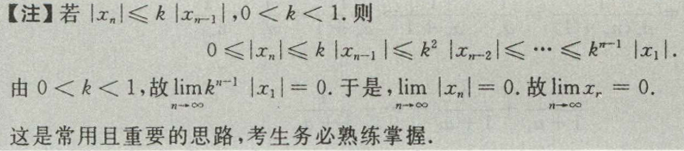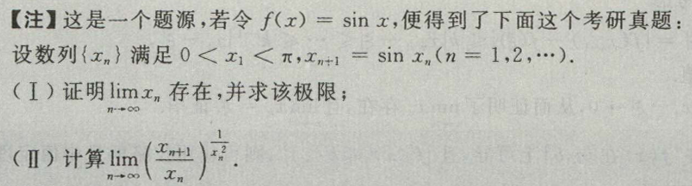2020张宇1000题·数一·刷题记录

第一篇高等数学

第1章极限、连续

三、数列极限(1.64-1.91)

换元，拆分，等价替换。
分母无理化，化简代值。
分母无理化，e的重要极限。
？？？拉格朗日中值定理。
两次比较，用夹逼定理卡值，最快。笨一点的方法，改写，然后求导化简估值。
要分x=0与不等于0两种情况，同乘sinx/2^n。
换元后，硬求导求两次。或者同1.67，用拉格朗日中值定理，函数差值转化为导数与差的乘积。
提取、化简、往e^x-1靠，再两次等价替换。
极限的保号性？？？有待细查。排除其他可举反例。
xₙ>0，所以数列xₙ有下界，是因为0肯定是xₙ的下界？？？
![](_v_images/20190918155455792_14057.png =460x)
若单调数列a_n有界，则极限存在，记$\lim \limits_{n \to \infty} a_n=A$，则$\lim \limits_{n \to \infty} \dfrac{1}{1+a_n^2}=\dfrac{1}{1+A^2}$，存在；若单调数列a_n无界，则极限不存在，$\lim \limits_{n \to \infty} a_n=+ \infty或-\infty$，此时有$\lim \limits_{n \to \infty} \dfrac{1}{1+a_n^2}=0$，存在。
(1)要被数列绕晕了；取倒数，两边同时减去一项，往b_n与b_n-1的关系上靠，真难想到啊。
(2)等比数列求和公式，${\displaystyle S_{n}={\begin{cases}{\frac {a_{1}-a_{1}q^{n}}{1-q}}&q\neq 1\\na_{1}&q=1\end{cases}}}$；求a_n的表达式需要用到b_n的和。猜猜(-1/2)^x的函数图像什么样？
a_n肯定是单调递增，用反证法可以证得a_n无上界。题目所给式子可以让1/a_n+1有两种变形，但是要往求和的式子上靠，用到了拆分。
看起来简单，结果又是一个令人大头的。证明$x_n>0$的过程，为啥要那样设，而且只在草稿纸上证明？？？先根据条件求得极限，再将假设代回验证，先斩后奏。？？？一系列骚操作变换，相间取绝对值-拆分-比较替换，往$x_n+1与x_n$的关系上靠，然后成功套路使用递归，但是最后为啥能直接去掉了绝对值？？？看懂了也做不来系列。
跟1.77只有第一步相同，先假设求值，舍去负值用的极限保号性？？？再相减取绝对值，不过这里是直接代值，接着通分后居然能提公因式，$1+(1-\sqrt2)(x_{n-1}+1)=(1-\sqrt2)(x_{n-1}-\sqrt2)$，然后一比较再化简，将分母变没了，真神。
![](_v_images/20190918192745784_19603.png =460x)

最后得到形式一模一样的$x_n+1与x_n$的关系，此步就是关键，也是最终目的，能成功套路使用递归。
![](_v_images/20190918200027946_25492.png =460x)
掌握套路就丝毫不慌了，跟1.77类似、1.78一模一样。
答案提供了另一种思路，用比值取绝对值化简，配合夹逼准则，解法内核是一样的。
不喜欢证明题啊，太抽象了，只知道跟介值定理有关，然后就无从下手了，呃，让我先跳过。？？？
(1)~~画图怎么感觉ξ不是唯一的，难道是画得不合理。~~？？？一番骚操作得到了函数值两端异号，然后就由连续函数介值定理，得证。再用反证法证明ξ的唯一性，又是一番骚操作。
(2)往已知条件上面靠，构造相减，然后运用递归，与1.81相同，$0< k< 1，|x_1-\xi|\geq 0，有\lim \limits_{n \to \infty}k^{n-1}=0，\lim \limits_{n \to \infty}x_n=\xi$得证。
总结拓展：题源的子题看起来就没那么难懂了。
(1)构造大函数，导数小于0，大函数单调递减。而且两端极限都是无穷，$\lim \limits_{x \to -\infty}F(x)=+\infty，\lim \limits_{x \to +\infty}F(x)=-\infty$，零点定理，得证。
(2)往$|x_n-\xi|与|x_{n-1}-\xi|$的关系上靠，同上，构造相减，运用递归。
先找$A_n+1，B_n+1与A_n，B_n$之间的关系，然后得到$x_n=\dfrac{A_n}{B_n}$的表达式，并看成一个整体，化简分式的时候只有一种方式能通。然后构造$x_{n+1}-x_n$，通分化简后观察式子，得到$x_{n+1}-x_n与x_n-x_{n+1}$同号的性质，这条信息很重要！能够确定数列$\{x_n\}$是单调的，从而确定极限存在，最后假设再代入求值，由极限的保号性，舍去负值。
(1)此题能通过$a_{n+1}-{a_n}$代换，从而确定数列单调递减。又易得$a_n \geq 0$，故数列肯定有下界，收敛得证。
(2)根据已知条件几步简单变形，$\lim \limits_{x \to \infty}$可以跨括号。？？？此时的t应该满足0< t< 1吧。
(3)易得t≥1，假设t≠0，与(2)的结论相矛盾，用反证法得证。
总结拓展：题源而改的考研真题看一下。
![](_v_images/20190919213244351_15891.png =460x)

(1)用到了x>0时，0<sinx<x的性质。为什么能直接说$0< x_n<\pi$？？？数学归纳法得到$0< x_{n+1}=sinx_n< x_n$，数列单调减少且$x_n> 0$，由单调有界准则知数列极限存在，故有$\lim \limits_{n \to \infty}x_{n+1}=\lim \limits_{n \to \infty}sinx_n$，得a=sina，a=0，所以数列极限为0。
(2)需要将$\lim \limits_{n \to \infty}\bigg(\dfrac{x_{n+1}}{x_n}\bigg)^\frac{1}{x_n^2}$转化为$\lim \limits_{x \to 0}\left(\dfrac{sinx}{x}\right)^\frac{1}{x^2}$，就是熟悉的求极限了。改写，拆分，等价替换，得到结果。
(1)题目突然简单，函数求导寻找驻点，还是唯一的，注意定义域，其实不用画图分析，函数的Wolfram图像验证。
(2)$将x_n跟x_{n+1}$分别展开，找二者间的关系，跟(1)的结论联系上了。推出数列有上界以及单调递增，数列极限存在得证。假设极限，再代入式子反求。
积分要拆成两部分之和，盲猜$x_n$应该是从1逐渐趋于0。证明的话需要找$x_n跟x_{n-1}$二者间的关系，化简$x_n$，然后找大小关系，确定数列单调有界，得出极限。？？？有个问题，$x_{n-1} \in (0,1)$是假设的，貌似没有确切证明，显而易见？
(1)明显是给第二问做铺垫，可以单独成题。直接画图易得，就不需要通过构造函数证单调取极值了。(滑稽)
(2)通过定义域以及代换能得到$0 \lt x_2 \lt ln2$，但是反而不需要这么精确，只需要$0 \lt x_2 \lt 1$这部分。同理可证$0 \lt x_k \lt 1$，数学归纳法得到$0 \lt x_n \lt 1$，数列有界。再通过已知条件证明数列单调减少，故极限存在。
(1)高中知识就可证得，利用函数单调性与几个关键点与0的大小。
(2)ξ是同一个，F(ξ)=0，先证$x_1 \gt x_2 \gt ξ$。？？？假设$x_{n-1} \gt x_n \gt ξ$成立，证明数列单调减少且有下界ξ，故极限存在。
(1)函数单调与零点定理。
(2)注意第一问的结论是任意n，取不同值对应的$x_n$，都是满足方程等于0的。所以有$f_{n+1}(x_{n+1})=e^{x_{n+1}}+x_{n+1}^{2(n+1)+1}=e^{x_{n+1}}+x_{n+1}^{2n+1} \cdot x_{n+1}^2=0$，注意$x_{n+1} \in (-1,0)$是小于0的，而$x_{n+1}^2 \in (0,1)$是大于0的，所以$e^{x_{n+1}}+x_{n+1}^{2n+1} \lt f_{n+1}(x_{n+1})=0$。而$f_n(x_n)=e^{x_n}+x_n^{2n+1}=0$，所以$\color{red}{e^{x_{n+1}}+x_{n+1}^{2n+1} \lt e^{x_n}+x_n^{2n+1}}$。注意此时x的指数都时2n+1，可以看成是固定的，而且$x\in(-1,0)$，$e^x+x^{2n+1}$又是单调递增的函数，所以有$x_{n+1} \lt x_n$，数列${x_n}$单调减少。？？？此步骤不容易看懂，主要是因为x的下标n与上标2n+1的n，需要区分开跟随变动和拆分后不变的情况。${x_n}$单调有下界，若极限存在，记$\lim \limits_{n \to \infty}x_n=a$，$e^{x_n}=-x_n^{2n+1}$，所以$\dfrac{x_n}{2n+1}=ln(-x_n)$。$n\to\infty$时，有$a \cdot 0=ln(-a)$，所以$\lim \limits_{n \to \infty}x_n=a=-1$。$$
(3)a还是上面的那个a，但是需要(2)问用到$x_n$的另一种变形，$x_n=-e^{\frac{x_n}{2n+1}}$，最终目的消去相乘的n。$\lim \limits_{n \to \infty}n(x_n-a)=\lim \limits_{n \to \infty}-n(e^{\frac{x_n}{2n+1}}-1)=\lim \limits_{n \to \infty}-n(\dfrac{x_n}{2n+1})=-\dfrac{a}{2}=\dfrac{1}{2}$。最后的替换是因为$\frac{x_n}{2n+1} \to 0，e^x-1 \sim x$。
两个大F的函数可以用来求出表达式，$x_{n+1}=\dfrac{x_n^2+9}{2x_n}=\dfrac{1}{2}(x_n+\dfrac{9}{x_n}) \geq \dfrac{1}{2} \cdot 2\sqrt{x_n \cdot \dfrac{9}{x_n}}=3$，所以数列有下界。而且$\color{red}{\dfrac{x_{n+1}}{x_n}=\dfrac{1}{2}(1+\dfrac{9}{x_n^2})} \leq 1$。此处$x_{n+1}$用公式替换，而$x_n$没有用公式替换，直接除，就不会出现$x_{n-1}$了，而且$x_n$跟$x_{n+1}$一样，都是$\geq3$的。于是证明了数列单调递减且有下界，设极限存在，有$A=\dfrac{A^2+9}{2A}，A=\pm3$，-3舍去，数列极限=3。