今天考的还是牛客 牛客的题的质量还是挺不错的 至少 我都不会qwq。
由于下一次的没有参加 所以这里把下一次的题也顺带说一下。(填坑期间。

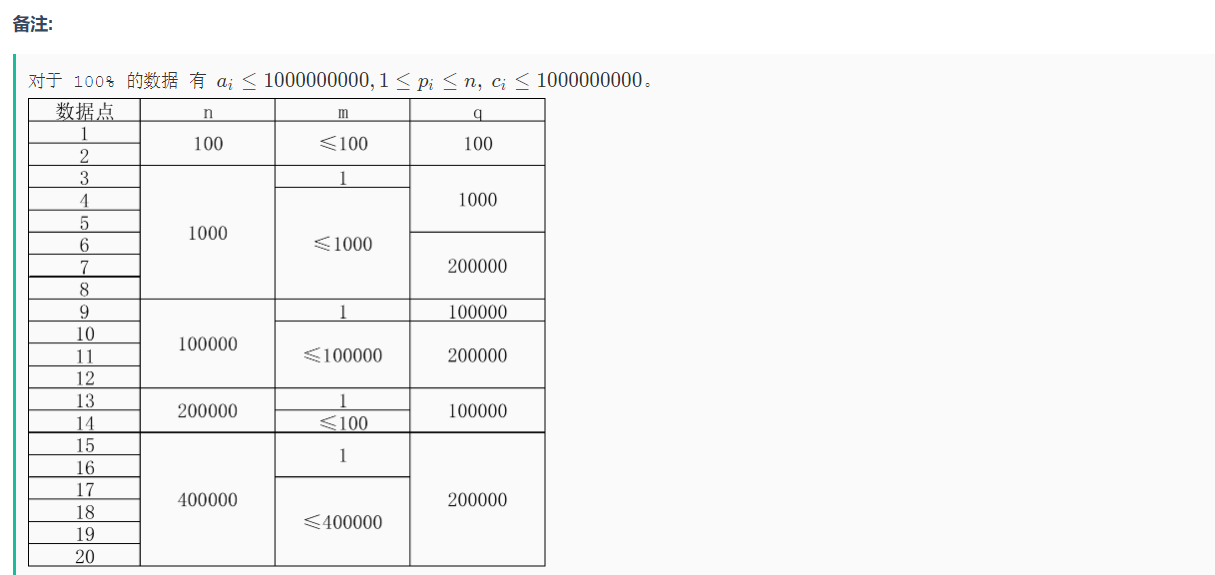
给人的感觉 类似于二分之后模拟。但是模拟的话也就是每次我们选择最多的需求开始做 然后这样 每次都选取最高的那个 然后慢慢填 这样效率并不高如何快速判定答案?
不知道 其实是这样的我们容易得到答案的下界max{ai}和 令一个答案的下界 ceil(sum/m) ceil 向上取整的意思。
取max我们得到了一个答案我们猜想 一下这个答案是否合法 ?其实花了几个样例发现是合法的就可以写了 。
证明是这样的我们依次给每一天分配 第一天分配a1 第二天从a1之后继续分配 然后如果不够就从头开始 由于答案>=max{ai}
这满足了一个限制一天不会被同一个机器做两次 不可能绕一圈还多 然后发现这样做就是合法的 然后由于总次数大于sum所以可以发现不会出现不够的情况 所以我们成功的构造出来了。
那就是动态查询最大值了 multiset即可。值得一提的是我是二分找答案了 爆longlong了。
直接除较好。

//#include<bits/stdc++.h>
#include<iostream>
#include<queue>
#include<iomanip>
#include<cctype>
#include<cstdio>
#include<deque>
#include<utility>
#include<cmath>
#include<ctime>
#include<cstring>
#include<string>
#include<cstdlib>
#include<vector>
#include<algorithm>
#include<stack>
#include<map>
#include<set>
#include<bitset>
#define INF 1000000000
#define ll long long
#define db double
#define pb push_back
#define un unsigned
#define mod 1000000007
#define ull unsigned long long
using namespace std;
char *fs,*ft,buf[1<<15];
inline char getc()
{
return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline ll read()
{
ll x=0,f=1;char ch=getc();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();}
return x*f;
}
const int MAXN=400010;
ll n,m,q;
ll a[MAXN];
ll sum;
multiset<ll>s;
multiset<ll>::iterator it;
inline ll ask()
{
ll maxx=*s.rbegin();
ll w=sum%m==0?sum/m:sum/m+1;
return max(w,maxx);
}
int main()
{
//freopen("1.in","r",stdin);
//freopen("1.out","w",stdout);
n=read();m=read();q=read();
for(int i=1;i<=n;++i)s.insert(a[i]=read()),sum+=a[i];
printf("%lld\n",ask());
for(int i=1;i<=q;++i)
{
ll x,y;
x=read();y=read();
it=s.find(a[x]);
s.erase(it);
sum-=a[x];
a[x]=y;
sum+=a[x];
s.insert(a[x]);
printf("%lld\n",ask());
}
return 0;
}


算是一道考验中级难度的图论题目吧 贪心挺容易看出来的 但是 对仙人掌 仙人掌沙漠 沙漠 迷的同学就不太友好了。
仙人掌 一张非常优秀的 图每条边最多属于一个简单的环 也就是不存在大环套小环的情况了。
考虑最优性 我们期望删除一条边 最多 能分出一个联通块 我们我们求出所有的点双联通分量也就是环 然后对环进行删。
然后先把割边删掉不必要非得求割边 因为考虑到一个大小为2的点双联通分量中间一定是割边 所以我们先删这个 剩下的从大到小删即可。

//#include<bits/stdc++.h>
#include<iostream>
#include<queue>
#include<iomanip>
#include<cctype>
#include<cstdio>
#include<deque>
#include<utility>
#include<cmath>
#include<ctime>
#include<cstring>
#include<string>
#include<cstdlib>
#include<vector>
#include<algorithm>
#include<stack>
#include<map>
#include<set>
#include<bitset>
#define INF 1000000000
#define ll long long
#define db double
#define pb push_back
#define un unsigned
#define mod 1000000007
#define ull unsigned long long
using namespace std;
char *fs,*ft,buf[1<<15];
inline char getc()
{
return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{
int x=0,f=1;char ch=getc();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();}
return x*f;
}
//满堂花醉三千客 一剑霜寒十四州.
const int MAXN=1000010;
int n,m,k;
int top,cnt,ans,rt,id,w,len=1;
int q[MAXN];
int s[MAXN];
int dfn[MAXN],low[MAXN],vis[MAXN];
int lin[MAXN],ver[MAXN<<2],nex[MAXN<<2];
inline int cmp(int x,int y){return x>y;}
inline void add(int x,int y)
{
ver[++len]=y;
nex[len]=lin[x];
lin[x]=len;
}
inline void dfs(int x)
{
dfn[x]=low[x]=++cnt;
s[++top]=x;
for(int i=lin[x];i;i=nex[i])
{
int tn=ver[i];
if(!dfn[tn])
{
dfs(tn);
low[x]=min(low[x],low[tn]);
if(low[tn]==dfn[x])
{
int sz=0;
for(int j;j!=tn;--top)
{
j=s[top];
++sz;
}
++sz;
if(sz==2){if(k)--k,++ans;}
else q[++id]=sz;
}
}
else low[x]=min(low[x],dfn[tn]);
}
}
int main()
{
//freopen("1.in","r",stdin);
n=read();m=read();k=read();
for(int i=1;i<=m;++i)
{
int x,y;
x=read();y=read();
add(x,y);add(y,x);
}
for(int i=1;i<=n;++i)
if(!dfn[i])
{
++ans;top=0;
dfs(i);
}
sort(q+1,q+1+id,cmp);
for(int i=1;i<=id;++i)
{
if(!k)break;
--k;
w=min(k,q[i]-1);
ans+=w;
k-=w;
}
printf("%d\n",ans);
return 0;
}


Ynoi 天降之物可还行qwq. 出毒瘤分块就没意思了 话说此题还真的没意思。
我觉得这道题很屑 所以就不说了。说下暴力/cy 觉得我的暴力很优秀。
这里强制在线不在线都是没有用的东西 无聊由于修改的存在 不存在一些离线的算法。
怎么求答案?我的想法是考虑归并的 对位置进行归并复杂度O(n) 但是这要求有序 把位置放到set里即可。
由于这里是O(n)set所以归并的复杂度是O(n)的 但是修改的话是nmlog的 很烦对吧。
考虑 一下无修改每次搞完 map存一下答案可大大降低复杂度 近乎应该是O(n~n^2)左右的 可以跑的很快所以这样就得到了50分。
100分做法很屑 毒瘤分块 然后处理块内的 和 块外的 然后 修改的话要整块打标记碎块就重构一部分。
总体复杂度 nsqrt(n)+msqrt(n) 。没写100分了 我觉得做法很屑。

//#include<bits/stdc++.h>
#include<iostream>
#include<queue>
#include<iomanip>
#include<cctype>
#include<cstdio>
#include<deque>
#include<utility>
#include<cmath>
#include<ctime>
#include<cstring>
#include<string>
#include<cstdlib>
#include<vector>
#include<algorithm>
#include<stack>
#include<map>
#include<set>
#include<bitset>
#define INF 1000000000
#define ll long long
#define db double
#define pb push_back
#define un unsigned
#define mod 1000000007
#define ull unsigned long long
#define pii pair<int,int>
#define mk(x,y) make_pair(x,y)
using namespace std;
char *fs,*ft,buf[1<<15];
inline char getc()
{
return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;
}
inline int read()
{
int x=0,f=1;char ch=getc();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();}
return x*f;
}
//满堂花醉三千客 一剑霜寒十四州
//注set均摊 O(n)
const int MAXN=100010;
int n,m,op,flag,last;
struct wy
{
int op;
int x,y;
int z;
}t[MAXN];
int pos[MAXN],w[MAXN];
int a[MAXN],b[MAXN];
set<int>s[MAXN];
set<int>::iterator it,lt;
map<pii,int>H;
inline int ask(int x,int y)
{
if(x==y)return 0;
int gg=INF;
int len1=s[x].size();
int len2=s[y].size();
it=s[x].begin();
lt=s[y].begin();
int len=len1+len2;
int i=1,j=len1+1;
int la=INF,lb=INF;
for(int k=1;k<=len;++k)
{
if(j>len||(i<=len1&&(*it)<(*lt)))
{
gg=min(gg,abs(*it-lb));
la=*it;++it;++i;
if(j==len+1)break;
}
else
{
gg=min(gg,abs(*lt-la)),lb=*lt;
++lt;++j;
if(i==len1+1)break;
}
}
return gg;
}
inline void change(int l,int r,int x)
{
for(int i=l;i<=r;++i)
{
if(x==pos[i])continue;
s[pos[i]].erase(i);
--w[pos[i]];
pos[i]=x;
++w[pos[i]];
s[x].insert(i);
}
}
int main()
{
//freopen("1.in","r",stdin);
//freopen("1.out","w",stdout);
n=read();m=read();op=read();
for(int i=1;i<=n;++i)
{
int x;
x=read();
pos[i]=x;++w[x];
s[x].insert(i);
}
for(int i=1;i<=m;++i)
{
t[i].op=read();
if(t[i].op==1)
{
t[i].x=read();t[i].y=read();t[i].z=read();
flag=1;
}
else
{
t[i].x=read();t[i].y=read();
}
}
if(!flag)//无修改操作直接归并 复杂度 感觉很低
{
for(int i=1;i<=m;++i)
{
int x=t[i].x^last;
int y=t[i].y^last;
if(!w[x]||!w[y]){printf("%d\n",-1);last=0;continue;}
int ans;
if(H[mk(x,y)])ans=H[mk(x,y)];
else ans=ask(x,y),H[mk(x,y)]=ans;
printf("%d\n",ans);
if(op)last=ans;
}
return 0;
}
else
{
for(int i=1;i<=m;++i)
{
if(t[i].op==1)
{
change(t[i].x^last,t[i].y^last,t[i].z^last);
}
else
{
int x=t[i].x^last;
int y=t[i].y^last;
if(!w[x]||!w[y]){printf("%d\n",-1);last=0;continue;}
int ans=ask(x,y);
printf("%d\n",ans);
if(op)last=ans;
}
}
return 0;
}
return 0;
}
