1. 问题
力扣数据中心有 n 台服务器,分别按从 0 到 n-1 的方式进行了编号。
它们之间以「服务器到服务器」点对点的形式相互连接组成了一个内部集群,其中连接 connections 是无向的。
从形式上讲,connections[i] = [a, b] 表示服务器 a 和 b 之间形成连接。任何服务器都可以直接或者间接地通过网络到达任何其他服务器。
「关键连接」是在该集群中的重要连接,也就是说,假如我们将它移除,便会导致某些服务器无法访问其他服务器。
请你以任意顺序返回该集群内的所有 「关键连接」。
示例 1: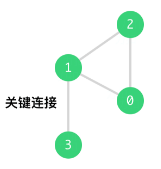
输入:n = 4, connections = [[0,1],[1,2],[2,0],[1,3]] 输出:[[1,3]] 解释:[[3,1]] 也是正确的。 原题链接;
2. Tarjan算法
Tarjan 算法是在一个图中查找强连通分量的算法。强连通分量是指,每个顶点皆可由该图上的边抵达其他的每一个点的有向图。
算法的基本思想:
任选一个节点开始进行深度优先搜索(若深度优先搜索结束后仍有未访问的节点,则从中任选一点再次进行)。搜索过程中已访问的节点不再访问。
强连通分量的根:
指深度优先搜索是强连通分量重首个被访问的节点。
为找到根节点,我们给每个节点 v 一个深度优先搜索标号 v.index ,表示第几个被访问的节点。此外,每个节点有一个值 v.lowlink,表示从 v 出发经边可到达的所有节点中最小的 index。 v.lowlink 总是不大于 v.index,且从 v 出发经有向边不能到达其他节点,v 是强连通分量的根当且仅当 v.lowlink = v.index.
伪代码:
algorithm tarjan is input: 图 G = (V, E) output: 以所在的强连通分量划分的顶点集合 index := 0 S := empty // 初始化栈S为空栈 for each v in V do if (v.index is undefined) strongconnect(v) end if function strongconnect(v) // 将未使用的最小index值作作为节点v的index v.index := index v.lowlink := index index := index + 1 S.push(v) // 考虑节点v的后继节点 for each (v, w) in E do if (w.index is undefined) then // 后继节点w未访问,递归调用 strongconnect(w) v.lowlink := min(v.lowlink, w.lowlink) else if (w is in S) then // w已在栈S中,则其也在当前的强连通分量中 v.lowlink := min(v.lowlink, w.index) end if // 若v是根则出栈,并得到一个强连通分量 if (v.lowlink = v.index) then start a new strongly connected component repeat w := S.pop() add w to current strongly connected component until (w = v) output the current strongly connected component end if end function 3. 本题解法
关键连接其实就是,除了强连通分量的其他边;也就是不形成闭环的边。
使用 time 表示该节点的索引; low 表示能到达的最小索引。
class Solution(object): def criticalConnections(self, n, connections): graph = [[] for _ in range(n)] for u, v in connections: graph[u].append(v) graph[v].append(u) seen = [False] * n time = [-1] * n low = [-1] * n t = [0] self.ans = [] def dfs(node, parent = None): seen[node] = True time[node] = low[node] = t[0] t[0] += 1 for nei in graph[node]: if nei == parent: continue if seen[nei]: low[node] = min(low[node], time[nei]) else: dfs(nei, node) low[node] = min(low[nei], low[node]) if low[nei] > time[node]: self.ans.append([node, nei]) for node, s in enumerate(seen): if not s: dfs(node) return self.ans 参考:
来源:51CTO
作者:rosefunR
链接:https://blog.csdn.net/rosefun96/article/details/100861403