- 概述
- 三角形的五心包括重心、垂心、外心、内心和旁心,是解决三角形问题的一种工具,也是一种研究对象。
- 前置知识:三角形等积变换、轴对称、相似、圆
- 内容
-
重心
- 重心的概念
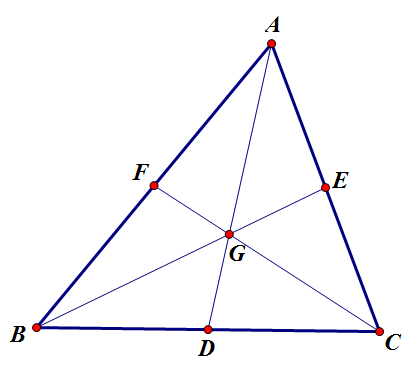
- 三角形三条中线的交点,叫做三角形的重心,三角形的重心在三角形的内部

如图,G为△ABC的重心
- 三角形三条中线的交点,叫做三角形的重心,三角形的重心在三角形的内部
- 重心的性质
- 基本性质
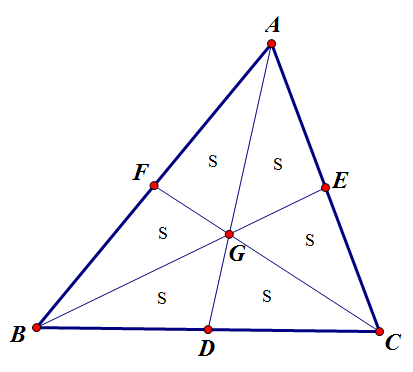
- 三角形重心与顶点的距离等于它与对应中点的距离的两倍,即$\displaystyle \frac{AG}{GD}=\frac{BG}{GE}=\frac{CG}{GF}=2$
- 证明1
- 由共边定理得

- 由蝴蝶定理得

- 于是有

- 由共边定理得$\frac{AG}{DG}=\frac{\triangle ACG}{\triangle CDG}=2$
- 同理可推得其他边的关系
- 由共边定理得
- 证明2
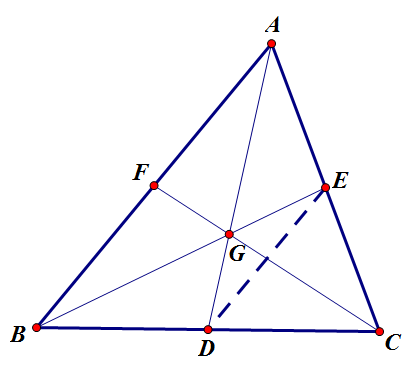
- 连接$DE$,由中位线得平行,得八字模型,由相似和中位线$\frac{1}{2}$得$2$倍

- 连接$DE$,由中位线得平行,得八字模型,由相似和中位线$\frac{1}{2}$得$2$倍
- 推论1
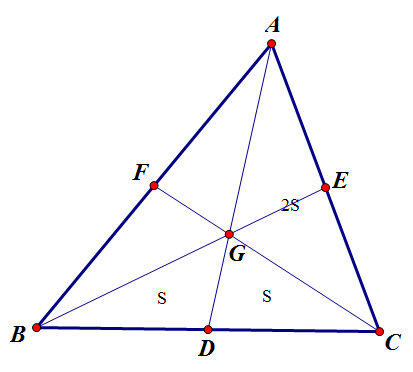
- 设$G$是$\triangle ABC$中一点,若$S_{\triangle ABG}=S_{\triangle ABC}=\frac{1}{3}S_{\triangle ABC}$,则$G$为$\triangle ABC$的重心
- 证明
- 由共边定理(燕尾模型)得$\frac{BD}{CD}=\frac{S_{\triangle ABG}}{S_{\triangle ACG}}=1$,即$G$为$\triangle ABC$中点
- 证明
- 设$G$是$\triangle ABC$中一点,若$S_{\triangle ABG}=S_{\triangle ABC}=\frac{1}{3}S_{\triangle ABC}$,则$G$为$\triangle ABC$的重心
- 基本性质
- 重心的概念
-
垂心
-
外心
-
内心
-
旁心
-