可能很多人不会留意到这个问题,今天恰好碰到了,然后来稍微讨论一下
直接插入排序应该是很多数据结构与算法书里第一个讲的排序算法,算法的描述是这样的:
把待排序列视作两段,一段是已排序列,一段是未排序列。每一趟排序时,为未排序列的首位在已排序列中进行查找(因为是直接插入排序,所以这里特指逐个比较)其合适的位置,然后将其插入(插入的过程中伴随着一系列元素的后移)。
当时没有想太多,直接写了个按文字描述的代码:
def InsertSort1(LIST): for i in range(1,len(LIST)):#从1开始,将0元素视为已排序列 TEMP=LIST[i]#保存中间变量 for ii in range(0,i): if LIST[ii]>TEMP:#从前往后逐次比较,如果出现比它大的元素,那么就说明他应该落在此位。此处未加等于号是为了保证排序稳定性 for iii in range(i,ii,-1):#注意,从后往前位移元素 LIST[iii]=LIST[iii-1] LIST[ii]=TEMP break return LIST
后来在看的时候发现好像不太对劲,怎么嵌套了三层for,于是乎回忆起了这一段应该是从后往前进行比较的
def InsertSort2(LIST): for i in range(1,len(LIST)): TEMP=LIST[i] flag=True for ii in range(i-1,-1,-1):#从后往前进行逐次比较 if LIST[ii]>TEMP: LIST[ii+1]=LIST[ii] else: LIST[ii+1]=TEMP flag=False break if flag: LIST[0]=TEMP return LIST
这里使用了两个辅助变量,TEMP和flag
事实上很多书在写这一段的时候,用了另一种巧妙的方法,只是用了一个辅助变量,这里可以参阅其他文章,我当时写到这里的时候立刻就回忆起了书里把这个做法叫做哨兵,即数组的0元素不用来储存元素,作为temp使用,在需要flag的地方不需要使用flag,保持了操作的一致性。这其实并不是我们要讨论的重点。
乍一看,二方法只嵌套了两层for,是不是比一方法要好呢?
答案是否定的,其实这个问题用一个图就能很好的表达了:
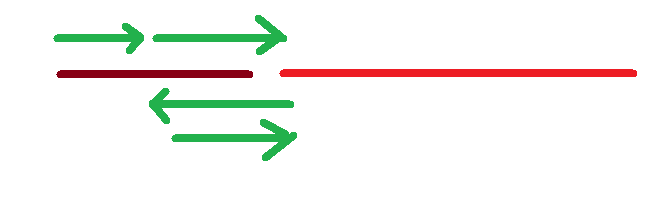
InsertSort1() 的性能十分稳定,在图中,它逐次比较的“路程”和后续位移的“路程”加起来恰好就是前一段线长(+1)
而InsertSort2()的性能不是那么稳定,在图中,当待排元素在已排序列中合适的位置靠后时,它的性能无疑是更好(付出了更短的“路程”),而当待排元素靠前时,它的性能就变差了(付出了双倍,更长的“路程”)
其实两个做法都是符合插入排序思想的,平均性能一致,最好性能的情况下2好于1,最坏情况下1>2
老实说真没想到这个最初始的算法会藏着这么一个有趣的小秘密,也算是颇有收获了