深度优先遍历简称DFS(Depth First Search),广度优先遍历简称BFS(Breadth First Search),它们是遍历图当中所有顶点的两种方式。
我们来到一个游乐场,游乐场里有11个景点。我们从景点0开始,要玩遍游乐场的所有景点,可以有什么样的游玩次序呢?
深度优先遍历
二叉树的前序、中序、后序遍历,本质上也可以认为是深度优先遍历。
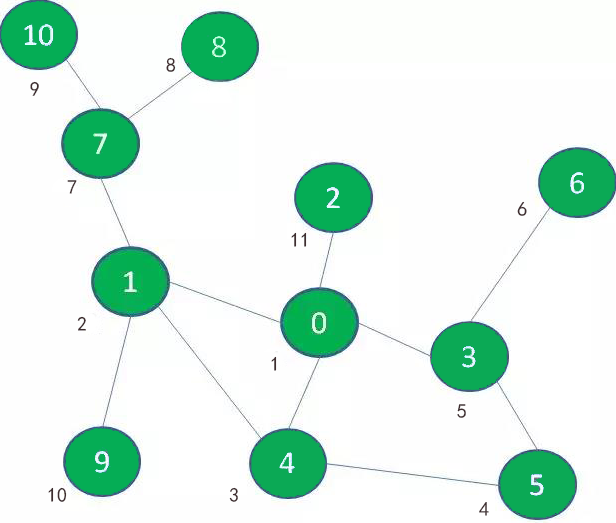
第一种是一头扎到底的玩法。我们选择一条支路,尽可能不断地深入,如果遇到死路就往回退,回退过程中如果遇到没探索过的支路,就进入该支路继续深入。
在图中,我们首先选择景点1的这条路,继续深入到景点4、景点5、景点3、景点6,终于发现走不动了(景点旁边的数字代表探索次序):
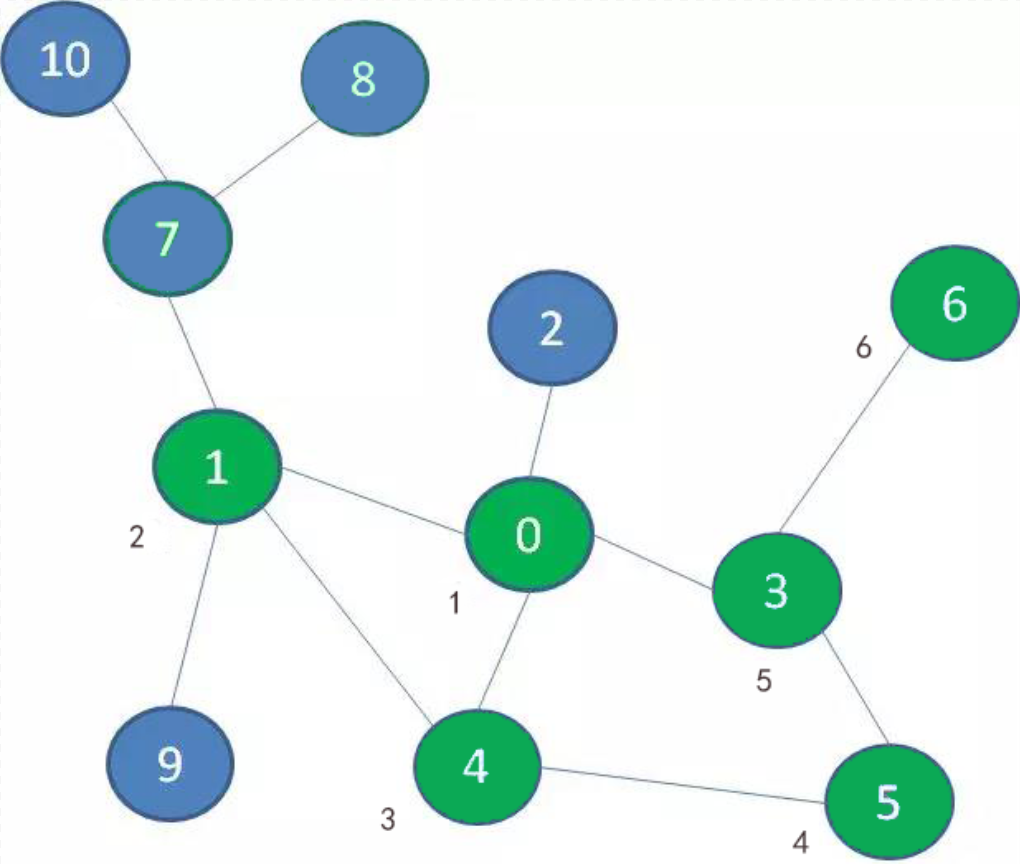
于是,我们退回到景点1,然后探索景点7,景点8,又走到了死胡同。于是,退回到景点7,探索景点10:
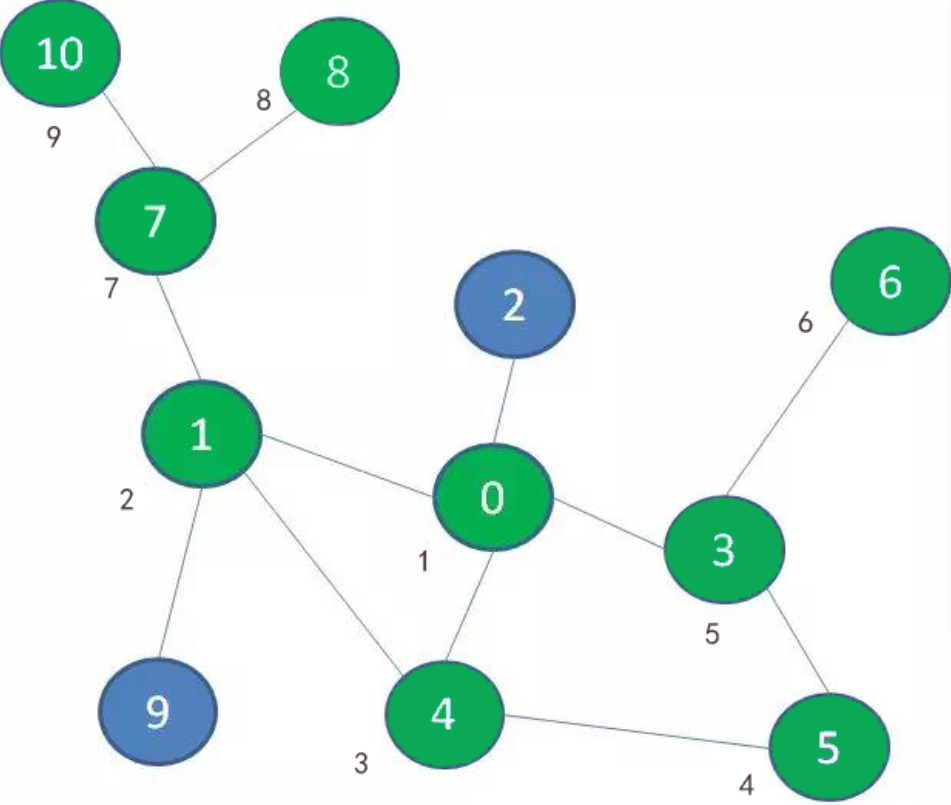
按照这个思路,我们再退回到景点1,探索景点9,最后再退回到景点0,后续依次探索景点2,终于玩遍了整个游乐场:
广度优先遍历
二叉树的层序遍历,本质上也可以认为是深度优先遍历。
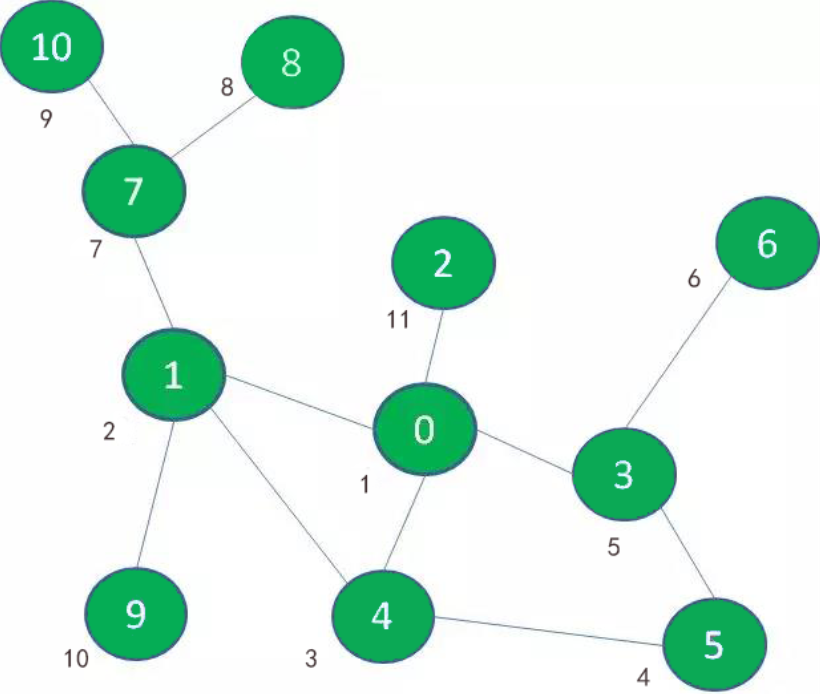
在图中,我们首先探索景点0的相邻景点1、2、3、4
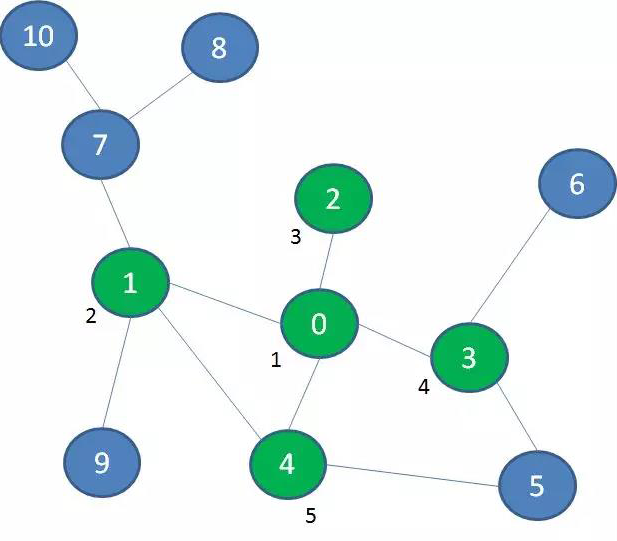
接着,我们探索与景点0相隔一层的景点7、9、5、6:
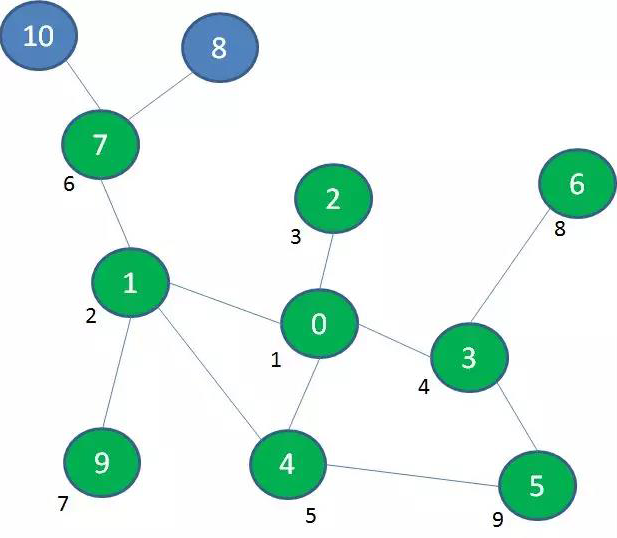
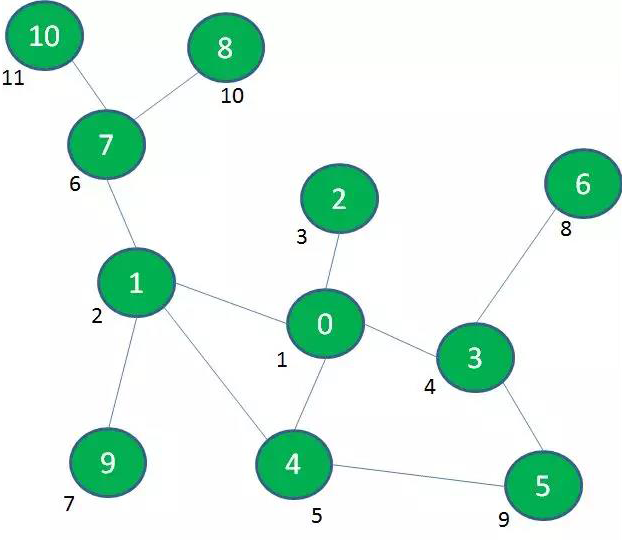
最后,我们探索与景点0相隔两层的景点8、10:
<?php
/**
* 图的深度优先遍历、广度优先遍历
* 图的存储结构--邻接矩阵
*/
class Graph {
// 存储节点信息
public $vertices;
// 存储边信息
public $arcs;
// 图的节点数
public $vexnum;
// 记录节点是否已被遍历
public $visited = [];
// 初始化
public function __construct($vertices) {
$this->vertices = $vertices;
$this->vexnum = count($this->vertices);
for ($i = 0; $i < $this->vexnum; $i++) {
for ($j = 0; $j < $this->vexnum; $j++) {
$this->arcs[$i][$j] = 0;
}
}
}
// 两个顶点间添加边(无向图)
public function addEdge($a, $b) {
if ($a == $b) { // 边的头尾不能为同一节点
return;
}
$this->arcs[$a][$b] = 1;
$this->arcs[$b][$a] = 1;
}
// 从第i个节点开始深度优先遍历
public function traverse($i) {
// 标记第i个节点已遍历
$this->visited[$i] = 1;
// 打印当前遍历的节点
echo $this->vertices[$i] . PHP_EOL;
// 遍历邻接矩阵中第i个节点的直接联通关系
for ($j = 0; $j < $this->vexnum ; $j++) {
// 目标节点与当前节点直接联通,并且该节点还没有被访问,递归
if ($this->arcs[$i][$j] == 1 && $this->visited[$j] == 0) {
$this->traverse($j);
}
}
}
//深度优先遍历
public function dfs() {
// 初始化节点遍历标记
$this->init();
// 从没有被遍历的节点开始深度遍历
for ($i = 0; $i < $this->vexnum; $i++) {
if ($this->visited[$i] == 0) {
// 若是连通图,只会执行一次
$this->traverse($i);
}
}
}
// 初始化节点遍历标记
public function init(){
for ($i = 0; $i < $this->vexnum; $i++) {
$this->visited[$i] = 0;
}
}
//广度优先遍历
public function bfs() {
// 初始化节点遍历标记
$this->init();
$queue = [];
for ($i = 0; $i < $this->vexnum; $i++) { // 对每一个顶点做循环
if (!$this->visited[$i]) { // 若是未访问过就处理
$this->visited[$i] = 1; // 设置当前顶点访问过
echo $this->vertices[$i] . PHP_EOL; // 打印顶点
$queue[] = $i; // 将此顶点入队列
while (!empty($queue)) { // 若当前队列不为空
$curr = array_shift($queue); // 将队对元素出队
for ($j = 0; $j < $this->vexnum; $j++) {
if ($this->arcs[$curr][$j] == 1 && $this->visited[$j] == 0) {
$this->visited[$j] = 1; // 将找到的此顶点标记为已访问
echo $this->vertices[$j] . PHP_EOL; // 打印顶点
$queue[] = $j; // 将找到的此顶点入队列
}
}
}
}
}
}
}
/*
0 1 2 3 4 5 6 7 8 9 10
0 0 1 1 1 1 0 0 0 0 0 0
1 1 0 0 0 1 0 0 1 0 1 0
2 1 0 0 0 0 0 0 0 0 0 0
3 1 0 0 0 0 1 1 0 0 0 0
4 1 1 0 0 0 1 0 0 0 0 0
5 0 0 0 1 1 0 0 0 0 0 0
6 0 0 0 1 0 0 0 0 0 0 0
7 0 1 0 0 0 0 0 0 1 0 1
8 0 0 0 0 0 0 0 1 0 0 0
9 0 1 0 0 0 0 0 0 0 0 0
10 0 0 0 0 0 0 0 1 0 0 0
so
0 1,2,3,4
1 0,4,7,9
2 0
3 0,5,6
4 0,1,5
5 3,4
6 3
7 1,8,10
8 7
9 1
10 7
*/
// 测试
$vertices = ['景点0', '景点1', '景点2', '景点3', '景点4', '景点5', '景点6', '景点7', '景点8', '景点9', '景点10'];
$graph = new Graph($vertices);
$graph->addEdge(0, 1);
$graph->addEdge(0, 2);
$graph->addEdge(0, 3);
$graph->addEdge(0, 4);
$graph->addEdge(1, 4);
$graph->addEdge(1, 7);
$graph->addEdge(1, 9);
$graph->addEdge(3, 5);
$graph->addEdge(3, 6);
$graph->addEdge(4, 5);
$graph->addEdge(7, 8);
$graph->addEdge(7, 10);
// 递归
echo "dfs:";
$graph->dfs();
echo "<br />";
echo "bfs:";
$graph->bfs();
来源:oschina
链接:https://my.oschina.net/u/4388412/blog/3452574