线性规划习题 | 易学教程

一、基础训练

<LT>例1</LT>已知$x,y$满足约束条件$\begin{cases}x+y-2\leq 0\x-2y-2\leq 0\2x-y+2\ge 0\end{cases}$,求解：

(1)$z=-\cfrac{1}{4}x+y$的最大值和最小值。

分析：将所给的目标函数改写成$l:y=\cfrac{1}{4}x+z$，则可以看到$z$的几何意义是直线$l$的纵截距，则直线$l$沿$y$轴向上平移，则$z$增大；直线$l$沿$y$轴向下平移，则$z$减小；故直线经过点$A(2,0)$时，$z_{max}=-\cfrac{1}{4}\times2+0=-\cfrac{1}{2}$；直线经过点$B(-2,-2)$时，$z_{min}=-\cfrac{1}{4}\times(-2)+(-2)=-\cfrac{3}{2}$；

(2)求$z=-\cfrac{1}{4}x-y$的最大值和最小值。

分析：将所给的目标函数改写成$l:y=-\cfrac{1}{4}x-z$，则可以看到$-z$的几何意义是直线$l$的纵截距，则直线$l$沿$y$轴向上平移，则$-z$增大，则$z$减小；直线$l$沿$y$轴向下平移，则$-z$减小，则$z$增大；故直线经过点$A(2,0)$时，$z_{min}=-\cfrac{1}{4}\times2-0=-\cfrac{1}{2}$；直线经过点$B(-2,-2)$时，$z_{max}=-\cfrac{1}{4}\times(-2)-(-2)=\cfrac{3}{2}$；

二、典例剖析

<LT>例2</LT>已知约束条件$\left{\begin{array}{1}{x-3y+4\leq 0}\ {x+2y-1 \ge 0 }\ {3x+y-8\leq 0} \end {array}\right.$，若目标函数$z=x+ay(a \ge 0)$恰好在点$(2，2)$处取到最大值，求$a$的取值范围。

提示：法1，线性规划法；法2：分离参数法。

<LT>例3</LT>已知$a>0$，$x，y$满足约束$\begin {cases} &x \ge 1 \ &x+y \leq 3 \ & y\ge a(x-3) \end {cases}$，若$z=3x+2y$的最小值为1，则$a$的值为__________.

<LT>例4</LT>【2016陕西省一检理科数学第11题】

设$k>1$，在约束条件$\begin{cases} &y\ge x \ &y\leq kx \ &x+y\leq 1\end{cases}$下，目标函数$z=x+ky$的最大值小于2，则$k$的取值范围是多少？

课件地址

分析：自行补图，由图像可知目标函数$y=-\cfrac{1}{k}x+\cfrac{z}{k}$的最优解是直线$y=kx$和$x+y=1$的交点$(\cfrac{1}{k+1}，\cfrac{k}{k+1})$，

代入得到$z_{max}=\cfrac{1}{k+1}+\cfrac{k^2}{k+1}<2$，化简得到$k^2-2k+1<2$，又$k>1$，故$k\in (1，1+\sqrt{2})$.

<LT>例4</LT>若目标函数$z=kx+2y$在约束条件$\begin{cases} &2x-y\leq 1 \ &x+y \ge 2 \ &y-x \leq 2\end{cases}$下仅在点$(1，1)$处取到最小值，则实数$k$的取值范围是多少

课件地址

分析：有图可知，仅在点$(1，1)$处取到最小值，只需目标函数$y=-\cfrac{k}{2}x+\cfrac{z}{2}$的斜率满足条件$-1<-\cfrac{k}{2}<2$即可，解得$k\in(-4，2)$；

引申：若题目变为：点$(1，1)$处取到最小值或取到最小值的最优解不唯一，可得到$k\in [-4，2]$；

<LT>例5</LT>已知函数$f(x)=\begin{cases} (\cfrac{1}{2})^x,&x<0 \ x-2,&x\ge 0 \end{cases}$，若$f[f(-2)]=a$，实数$x，y$满足约束条件$\begin{cases} & x-a \ge 0 \ & x+y\leq 6 \ & 2x-y\leq 6\end{cases}$，则目标函数$z=\cfrac{3x+4y+10}{x+2}$的最大值是_________.

分析：先求得$a=2$，再代入做出可行域如图，课件地址

由可行域可以看出$k=\cfrac{y+1}{x+2}\in [-\cfrac{1}{4}，\cfrac{5}{4}]$，再将目标函数变形$z=\cfrac{3x+4y+10}{x+2}=\cfrac{3(x+2)+4y+4}{x+2}=3+4\times\cfrac{y+1}{x+2}$，从而可以计算出$z\in [2，8]$.

<LT>例6</LT>若$z=f(x,y)$称为二元函数，已知$f(x,y)=ax+by$，$\begin{cases} &f(1,-2)-5 \leq 0 \ &f(1,1)-4\leq 0 \ &f(3,1)-10 \ge0\end{cases}$ ，则$z=f(-1,1)$的最大值等于( )

分析：由题目已知，能很快转化为在线性约束条件$\begin{cases} &a-2b-5 \leq 0 \ &a+b-4\leq 0 \ &3a+b-10 \ge 0\end{cases}$下，求目标函数$z=f(-1,1)=-a+b$的最大值问题。余下解答略。

<LT>例7</LT>(2016全国第三次大联考第12题)

设P是不等式组$\begin{cases}x\ge 0\y\ge 0\x+3y\leq 1\end{cases}$表示的平面区域内的任意一点，向量$\vec{m}=(-1，1)$，$\vec{n}=(2，-1)$，若$\overrightarrow{OP}=\lambda\vec{m}+\mu\vec{n}$，则$\cfrac{\mu}{\lambda+1}$的取值范围是多少？

<img src="http://images2017.cnblogs.com/blog/992978/201709/992978-20170928220040590-607906064.png" /> 分析：由$\overrightarrow{OP}=(x，y)=(-\lambda+2\mu，\lambda-\mu)$；

则有$x=-\lambda+2\mu，y=\lambda-\mu$代入已知的线性约束条件，

得到$\begin{cases}-\lambda+2\mu\ge 0\\lambda-\mu\ge 0\-\lambda+2\mu+3(\lambda-\mu)\leq 1\end{cases}$，求$\cfrac{\mu}{\lambda+1}$的取值范围，

即相当于已知$\begin{cases}x-2y\leq 0\x-y\ge 0 \ 2x-y\leq1\end{cases}$，求$k=\cfrac{y-0}{x-(-1)}$的取值范围，

如右图所示，故$k_{min}=k_{BO}=0$，$k_{max}=k_{BA}=\cfrac{1-0}{1+1}=\cfrac{1}{2}$，

故$\cfrac{\mu}{\lambda+1}$的取值范围为$[0，\cfrac{1}{2}]$。

<LT>例8</LT>【向量的投影的几何意义】【2018西安八校联考第5题】

已知$O$是坐标原点，点$A(2，1)$，点$M(x，y)$是平面区域$\begin{cases}&y\leq x\&x+y\leq 1\&y\ge -1\end{cases}$内的一个动点，则$\overrightarrow{OA}\cdot \overrightarrow{OM}$的最大值是多少？

法1：利用向量的坐标运算得到，$\overrightarrow{OA}\cdot \overrightarrow{OM}=2x+y$，故转化为求$2x+y$的最大值，即求$z=2x+y$的最大值，用线性规划的常规方法解决即可。

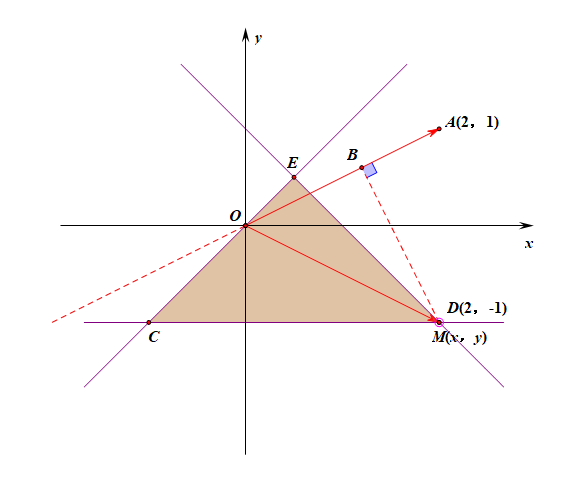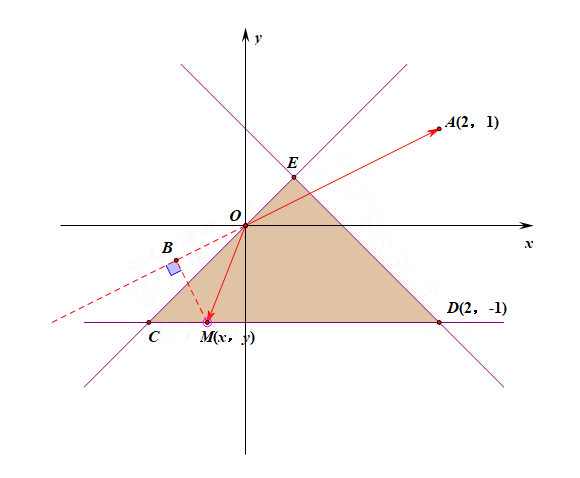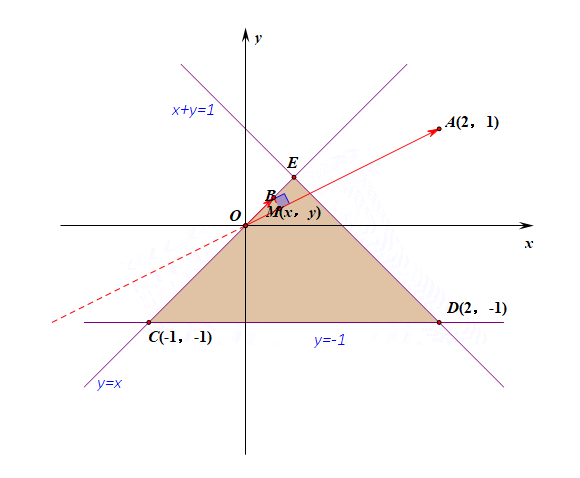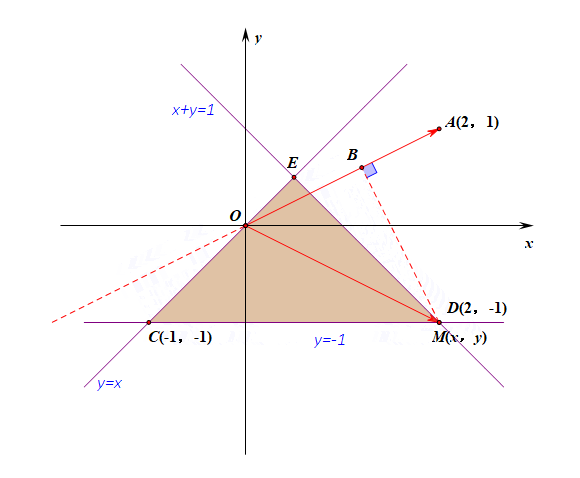
法2：利用向量的投影的几何意义求解，说明：点$M$是三角形区域内部及边界上的一个动点，动画只做了点$M$在边界上的情形；

注：图中有向线段$OB$是向量$\overrightarrow{OM}$在向量$\overrightarrow{OA}$方向上的投影，它是可正，可负，可零的；

$\overrightarrow{OA}\cdot \overrightarrow{OM}=|\overrightarrow{OA}|\cdot |\overrightarrow{OM}|\cdot cos\theta$，其中$|\overrightarrow{OA}|$是个定值，

故只需要求$|\overrightarrow{OM}|\cdot cos\theta$的最大值，而$|\overrightarrow{OM}|\cdot cos\theta$的几何意义是$\overrightarrow{OM}$在$\overrightarrow{OA}$方向上的投影，

由图形可知，当点$M(x，y)$位于点$(2，-1)$时投影$|\overrightarrow{OM}|\cdot cos\theta$最大，故将点$(2，-1)$代入$\overrightarrow{OA}\cdot \overrightarrow{OM}=3$。

变式题1：求$\overrightarrow{OA}\cdot \overrightarrow{OM}$的最小值是多少？

分析：由上图可以看出，当两个向量的夹角为钝角时，其投影是负值，故当点$M$位于点$C$时，其内积最小，

此时将点$(-1，-1)$代入得到$\overrightarrow{OA}\cdot \overrightarrow{OM}=-3$。

变式题2：求向量$\overrightarrow{OM}$的投影的绝对值最小时的动点$M$的轨迹方程？

分析：当其夹角为$90^{\circ}$时，有向线段$OB=0$，故向量$\overrightarrow{OM}$的投影的绝对值最小$0$；

此时，点$M$在三角形区域内部且和直线$OA$垂直，故其轨迹为$y=-2x，(-1\leqslant y\leqslant 0)$

<LT>例9</LT>函数$y=x^3+3ax^2+3bx$在区间$[-1，1]$单调减少，且$a＞0$，则$2a+b$的最大值为________．

【分析】先由函数单调递减转化为恒成立，再转化为线性规划问题求解。

【解答】

由函数$y=x^3+3ax^2+3bx$在区间$[-1，1]$单调减少，

可得$f'(x)=3x^2+6ax+3b\leq 0$在$[-1，1]$上恒成立，

即$\left{\begin{array}{l}{f'(-1)\leq 0}\{f'(1)\leq 0}\end{array}\right.$，

即$\left{\begin{array}{l}{3-6a+3b\leq 0}\{3+6a+3b\leq 0}\end{array}\right.$，

又$a>0$，得到

$\left{\begin{array}{l}{2a-b-1\ge 0}\{2a+b+1\leq 0}\{a>0}\end{array}\right.$，

做出可行域如右图，由图可知，当直线$z=2a+b$，即$b=-2a+z$平移和直线$2a+b+1= 0$平行时，

$2a+b$取到最大值，最大值为$-1$。

本题容易受$a>0$的影响，即点$(0，-1)$不在可行域内，

但可以在直线$2a+b+1=0$上另外取一点代入求值。

【点评】当利用恒成立转化为线性规划问题后，题目的难度就降低了。同时提醒注意由恒成立命题向二次不等式组转化的这一数学模型，希望大家能理解记忆，以后碰到就可以直接应用。

<LT>例10</LT>已知实数$a、b$满足条件$\left{\begin{array}{l}{a+b-2\ge 0}\{b-a-1\leq 0}\{a\leq 1}\end{array}\right.$，求$\cfrac{a+2b}{2a+b}$的取值范围。

【法1】转化为斜率型，

思路如下：由于所求值函数为分式形式的关于$a、b$的一次齐次式，

故可以转化为$\cfrac{a+2b}{2a+b}=\cfrac{1+2\cdot \cfrac{b}{a}}{2+\cfrac{b}{a}}$，

$=2-\cfrac{3}{2+k}=f(k)$，其中$k=\cfrac{b}{a}$

这样先由可行域求得$k=\cfrac{b}{a}\in [1，3]$

函数$f(k)$在区间$[1，3]$上单调递增，

然后用单调性，求得$\cfrac{a+2b}{2a+b}\in [1，\cfrac{7}{5}]$

【法2】换元法，令$a+2b=n$，$2a+b=m$，

联立解以$a、b$为元的方程组，得到

$a=\cfrac{2m-n}{3}$，$b=\cfrac{2n-m}{3}$，

代入原不等式组，可将原约束条件转化为关于$m 、n$的不等式组，

即已知$m 、n$满足条件$\left{\begin{array}{l}{m+n-6\ge 0}\{n-m-1\leq 0}\{2m-n-3\leq 0}\end{array}\right.$，

求$\cfrac{n}{m}$的取值范围。

利用数形结合思想可得，$\cfrac{a+2b}{2a+b}=\cfrac{n}{m}\in [1，\cfrac{7}{5}]$。图像

<LT>例11</LT>已知实数$x$，$y$满足$\left{\begin{array}{l}{x^2+y^2\leq 9}\{x\ge 1}\{y\ge 1}\end{array}\right.$，则$\cfrac{y}{x-5}$的取值范围是____________。

分析：如图所示，从数上理解$\cfrac{y}{x-5}=\cfrac{y-0}{x-5}$，从形上理解，应该是定点$A(5，0)$和动点$P(x，y)$的连线的斜率的取值范围；

故当$k_{AP}$最大时，点$P$坐标应该为$(1，1)$，此时$k_{max}=-\cfrac{1}{4}$；

当$k_{AP}$最小时，点$P$位于直线$y=k(x-5)$和函数$y=\sqrt{9-x^2}$相切的切点$Q$处，以下重点求切点$Q(x_0，y_0)$的坐标；

法1：连结$OQ$，可知$|OQ|=3$，$|AQ|=4$，利用等面积法，可知$y_0=\cfrac{12}{5}$，代入函数$y=\sqrt{9-x^2}$求得$x_0=\cfrac{9}{5}$，故$k_{min}=k_{AQ}=-\cfrac{3}{4}$

故所求范围是$[-\cfrac{3}{4}，-\cfrac{1}{4}]$；

法2：利用导数求切点$Q(x_0，y_0)$的坐标；

由于$y=g(x)=\sqrt{9-x^2}$，则$g'(x)=\cfrac{1}{2}\cdot (9-x^2)^{-\cfrac{1}{2}}\cdot (-2x)=\cfrac{-x}{\sqrt{9-x^2}}$，

则$k=\cfrac{-x_0}{\sqrt{9-x_0^2}}$①，$y_0=k(x_0-5)$②，$y_0=\sqrt{9-x_0^2}$③，联立①②③，解得$x_0=\cfrac{9}{5}$，

代入函数$y=\sqrt{9-x^2}$，求得$y_0=\cfrac{12}{5}$，故$k_{min}=k_{AQ}=-\cfrac{3}{4}$，

故所求范围是$[-\cfrac{3}{4}，-\cfrac{1}{4}]$；

<LT>例13</LT>【2019届高三理科数学二轮用题】已知不等式组$\left{\begin{array}{l}{2x-y\ge 0}\{2-2y\leq 0}\{x\leq 2}\end{array}\right.$所表示的区域为$\Omega$，则区域$\Omega$的外接圆的面积为__________.

分析：做出如图所示的三角形可行域，三条边长可知，故求其外接圆的半径可以采用$S_{\triangle OAB}=\cfrac{abc}{4R}$，

又由于$S_{\triangle OAB}=\cfrac{1}{2}\times 3\times 2=3$，则$3=\cfrac{3\times \sqrt{5}\times 2\sqrt{5}}{4R}$，解得$R=\cfrac{5}{2}$，故$S_{外接圆}=\cfrac{25\pi}{4}$。

解后反思：结合题目的具体条件，选择恰当的公式，计算量能相应的减少。

<LT>例14</LT>【2019届高三理科数学三轮用题】

<LT>例15</LT>【2019届高三理科数学第三轮模拟训练题】实数$x$，$y$满足$\left{\begin{array}{l}{y\leqslant 2x+2}\{x+y-2\geqslant 0}\{x\leqslant 2}\end{array}\right.$，则$z=|x-y|$的最大值为【】

分析：先用常规方法求得$m=x-y$的取值范围，可得$m\in [-4，2]$，则$z=|m|\in [0，4]$，故选$B$。

<LT>例16</LT>已知$x^2+y^2\leq 1$，求$|2x+y-2|+|x+3y-6|$的最小值？

思路一：转化为点线距

为什么想到这个，我们发现$|2x+y-2|+|x+3y-6|=\sqrt{5}\cfrac{|2x+y-2|}{\sqrt{5}}+\sqrt{10}\cfrac{|x+3y-6|}{\sqrt{10}}$，

其中表达式$\cfrac{|2x+y-2|}{\sqrt{5}}$和$\cfrac{|x+3y-6|}{\sqrt{10}}$分别表示园内及圆上的动点到两条直线的距离，所以可以把“数”的问题转化为“形”的问题。

思路二：三角代换，令$x=R\cos\theta，y=R\sin\theta，R\in[0，1]$，则$|2x+y-2|+|x+3y-6|\ge|3R\cos\theta+4R\sin\theta-8|=|5R\sin(\theta+\phi)-8|$

思路三：

来源：oschina

链接：https://my.oschina.net/u/4295895/blog/3834074

标签

cos