量子纠缠2——CHSH不等式

问题

有Alice和Bob两个人，随机给他们两个数x和y(0或1)，然后A和B根据他们得到数(x和y)给两个个数a和b(0或1)。

规则如下：

如果输入的x和y都是1，那么，Alice和Bob给出不一样的数获胜；否则，Alice和Bob给出相同的数获胜。

Alice和Bob在拿到x和y后就不能交谈了，但是在拿到前可以交流。

问：Alice和Bob怎样约定获胜的可能性最大？

一共有以下十六中情况：

x	y	a	b	result
0	0	0	0	赢
0	0	0	1	输
0	0	1	0	输
0	0	1	1	赢
0	1	0	0	赢
0	1	0	1	输
0	1	1	0	输
0	1	1	1	赢
1	0	0	0	赢
1	0	0	1	输
1	0	1	0	输
1	0	1	1	赢
1	1	0	0	输
1	1	0	1	赢
1	1	1	0	赢
1	1	1	1	输

经典解法

我们可以看到，如果Alice和Bob随机输出a和b，即输出的a和b与输入的x和y无关，那么他们获胜了可能性是50%，也就是0.5。

如果有提前约定呢？

当输入x和y都是0的时候，Alice和Bob可以约定都出0（约定都出1也是一样的道理），这样，输入是（0，0）的25%可能是一定获胜。

但是当你的输入是1的时候，你不知道另一个人是的输入是0还是1。

如果约定出0，即，无论输入是什么都出0，则，获胜的可能性是75%，只有输入是（1，1）时失败。

如果约定出1，即，输入什么输出什么，则获胜的可能性是25%，只有输入是（0，0）才获胜。

如果约定一个出0一个出1（假设A遇1出1，B遇1出0），则成功率75%，只有在输入是（1，0）时失败。

综上，在经典解法中，成功的概率最大是0.75。

量子解法

首先我们给Alice和Bob一对bell态的量子比特（\(|\psi\rangle=\frac{1}{\sqrt2}|00\rangle + \frac{1}{\sqrt2}|11\rangle=\frac{1}{\sqrt2}|++\rangle + \frac{1}{\sqrt2}|--\rangle\)）

然后他们分别根据自己的输入对自己量子比特测量，测量结果就是他们的输出。

测量方式如下：

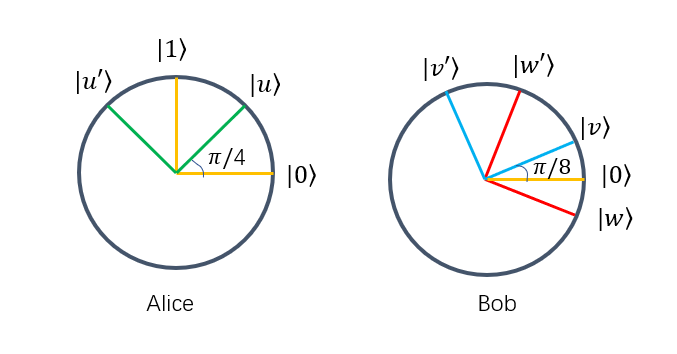
如果Alice的输入是0，那么就在\(| 0\rangle\)、\(| 1\rangle\)基测量，如果输入是1，就在\(| u\rangle\)、\(| u'\rangle\)基测量。

如果Bob的输入是0，那么就在\(| v\rangle\)、\(| v'\rangle\)基测量，如果输入是1，就在\(| w\rangle\)、\(| w'\rangle\)基测量。

这样的获胜的可能性是多少呢？

如果输入是（0，0）：因为Alice的输入是0，所以Alice用\(| 0\rangle\)、\(| 1\rangle\)基测量，测量在不在\(| 0\rangle\)，在的话输出1，不在输出0，并且可以知道他在\(| 1\rangle\)。此时，因为Alice和bob的量子是纠缠的，Bob的量子比特也会坍缩到\(| 0\rangle\)或者\(| 1\rangle\)的位置。Bob的输入也是0，所以Bob要在\(| v\rangle\)、\(| v'\rangle\)基测量，看量子在不在\(| v\rangle\)。如果Alice的量子最终坍缩到了\(| 0\rangle\)，在\(| v\rangle\)测量得到1的概率为\(cos^2\frac{\pi}{8}\)，因为\(| 0\rangle\)和\(| v\rangle\)之间的夹角是\(\frac{\pi}{8}\)，则有\(cos^2\frac{\pi}{8}\)的概率成功，如果Alice的量子坍缩到了\(| 1\rangle\)，则Alice的输出为0，在在\(| v\rangle\)测量得到1的概率为\(cos^2\frac{3\pi}{8}\)，但是这个时候输出0才会获胜，所以成功的概率依旧是\(cos^2\frac{3\pi}{8}\)。

其他输入的情况，按照上述过程，获胜的概率也都是\(cos^2\frac{3\pi}{8}\)，则总的获胜概率是\(cos^2\frac{3\pi}{8} \approx 0.85\)

结论

量子解法的最大成功率 \(>\) 经典解法的最大成功率

\[0.85 > 0.75 \]

量子纠缠存在

参考资料：

Quantume Mechanics & Quantume Computation Lecture 4

来源：oschina

链接：https://my.oschina.net/u/4312499/blog/4357666