　　　　在强化学习（十）Double DQN (DDQN)中，我们讲到了DDQN使用两个Q网络，用当前Q网络计算最大Q值对应的动作，用目标Q网络计算这个最大动作对应的目标Q值，进而消除贪婪法带来的偏差。今天我们在DDQN的基础上，对经验回放部分的逻辑做优化。对应的算法是Prioritized Replay DQN。

　　　　本章内容主要参考了ICML 2016的deep RL tutorial和Prioritized Replay DQN的论文<Prioritized Experience Replay>(ICLR 2016)。

1. Prioritized Replay DQN之前算法的问题

　　　　在Prioritized Replay DQN之前，我们已经讨论了很多种DQN，比如Nature DQN， DDQN等，他们都是通过经验回放来采样，进而做目标Q值的计算的。在采样的时候，我们是一视同仁，在经验回放池里面的所有的样本都有相同的被采样到的概率。

　　　　但是注意到在经验回放池里面的不同的样本由于TD误差的不同，对我们反向传播的作用是不一样的。TD误差越大，那么对我们反向传播的作用越大。而TD误差小的样本，由于TD误差小，对反向梯度的计算影响不大。在Q网络中，TD误差就是目标Q网络计算的目标Q值和当前Q网络计算的Q值之间的差距。

　　　　这样如果TD误差的绝对值$|\delta(t)|$较大的样本更容易被采样，则我们的算法会比较容易收敛。下面我们看看Prioritized Replay DQN的算法思路。

2. Prioritized Replay DQN算法的建模

　　　　Prioritized Replay DQN根据每个样本的TD误差绝对值$|\delta(t)|$，给定该样本的优先级正比于$|\delta(t)|$，将这个优先级的值存入经验回放池。回忆下之前的DQN算法，我们仅仅只保存和环境交互得到的样本状态，动作，奖励等数据，没有优先级这个说法。

　　　　由于引入了经验回放的优先级，那么Prioritized Replay DQN的经验回放池和之前的其他DQN算法的经验回放池就不一样了。因为这个优先级大小会影响它被采样的概率。在实际使用中，我们通常使用SumTree这样的二叉树结构来做我们的带优先级的经验回放池样本的存储。

　　　　具体的SumTree树结构如下图：

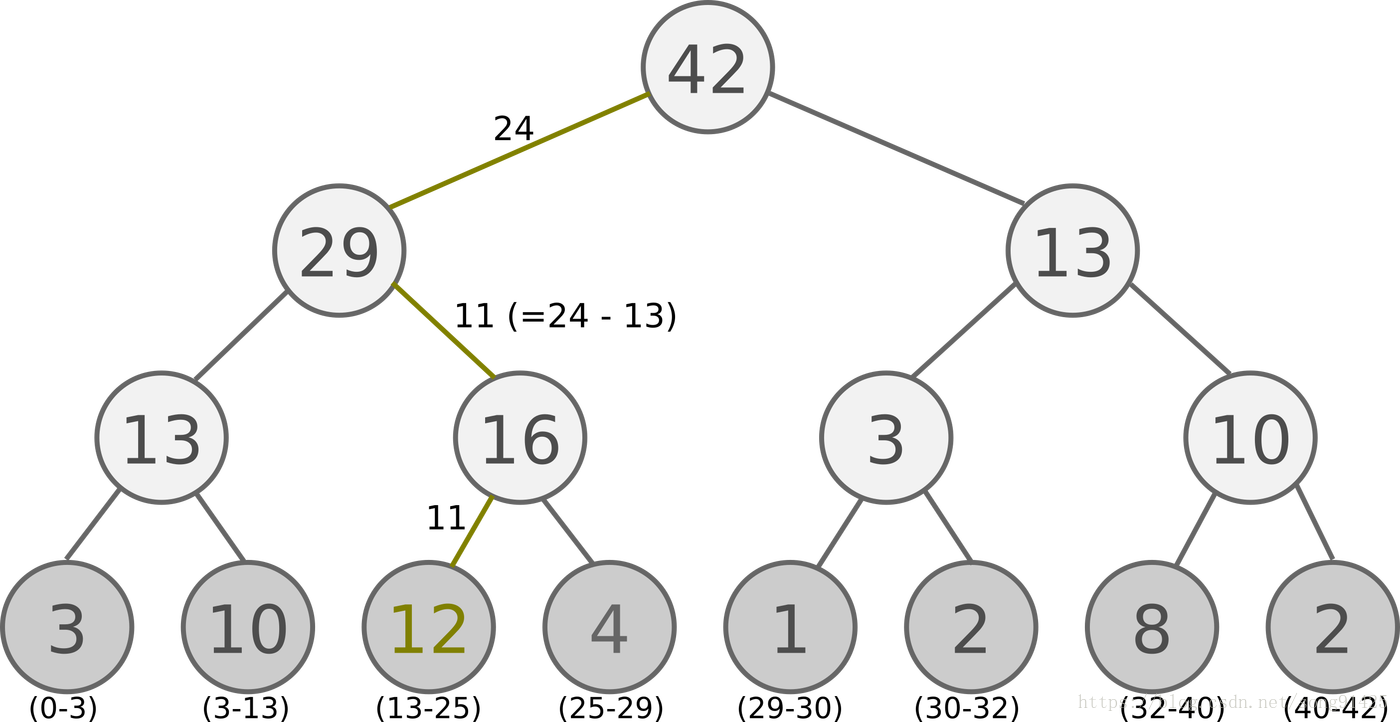
　　　　所有的经验回放样本只保存在最下面的叶子节点上面，一个节点一个样本。内部节点不保存样本数据。而叶子节点除了保存数据以外，还要保存该样本的优先级，就是图中的显示的数字。对于内部节点每个节点只保存自己的儿子节点的优先级值之和，如图中内部节点上显示的数字。

　　　　这样保存有什么好处呢？主要是方便采样。以上面的树结构为例，根节点是42，如果要采样一个样本，那么我们可以在[0,42]之间做均匀采样，采样到哪个区间，就是哪个样本。比如我们采样到了26，在（25-29）这个区间，那么就是第四个叶子节点被采样到。而注意到第三个叶子节点优先级最高，是12，它的区间13-25也是最长的，会比其他节点更容易被采样到。

　　　　如果要采样两个样本，我们可以在[0,21],[21,42]两个区间做均匀采样，方法和上面采样一个样本类似。

　　　　类似的采样算法思想我们在word2vec原理(三) 基于Negative Sampling的模型第四节中也有讲到。

　　　　除了经验回放池，现在我们的Q网络的算法损失函数也有优化，之前我们的损失函数是：$$\frac{1}{m}\sum\limits_{j=1}^m(y_j-Q(\phi(S_j),A_j,w))^2$$

　　　　现在我们新的考虑了样本优先级的损失函数是$$\frac{1}{m}\sum\limits_{j=1}^mw_j(y_j-Q(\phi(S_j),A_j,w))^2$$

　　　　其中$w_j$是第j个样本的优先级权重，由TD误差$|\delta(t)|$归一化得到。

　　　　第三个要注意的点就是当我们对Q网络参数进行了梯度更新后，需要重新计算TD误差，并将TD误差更新到SunTree上面。

　　　　除了以上三个部分，Prioritized Replay DQN和DDQN的算法流程相同。

3. Prioritized Replay DQN算法流程

　　　　下面我们总结下Prioritized Replay DQN的算法流程，基于上一节的DDQN，因此这个算法我们应该叫做Prioritized Replay DDQN。主流程参考论文<Prioritized Experience Replay>(ICLR 2016)。

　　　　算法输入：迭代轮数$T$，状态特征维度$n$, 动作集$A$, 步长$\alpha$，采样权重系数$\beta$，衰减因子$\gamma$, 探索率$\epsilon$, 当前Q网络$Q$，目标Q网络$Q'$, 批量梯度下降的样本数$m$,目标Q网络参数更新频率$C$, SumTree的叶子节点数$S$。

　　　　输出：Q网络参数。

　　　　1. 随机初始化所有的状态和动作对应的价值$Q$. 随机初始化当前Q网络的所有参数$w$,初始化目标Q网络$Q'$的参数$w' = w$。初始化经验回放SumTree的默认数据结构，所有SumTree的S个叶子节点的优先级$p_j$为1。

　　　　2. for i from 1 to T，进行迭代。

　　　　　　a) 初始化S为当前状态序列的第一个状态, 拿到其特征向量$\phi(S)$

　　　　　　b) 在Q网络中使用$\phi(S)$作为输入，得到Q网络的所有动作对应的Q值输出。用$\epsilon-$贪婪法在当前Q值输出中选择对应的动作$A$

　　　　　　c) 在状态$S$执行当前动作$A$,得到新状态$S'$对应的特征向量$\phi(S')$和奖励$R$,是否终止状态is_end

　　　　　　d) 将$\{\phi(S),A,R,\phi(S'),is\_end\}$这个五元组存入SumTree

　　　　　　e) $S=S'$

　　　　　　f) 从SumTree中采样$m$个样本$\{\phi(S_j),A_j,R_j,\phi(S'_j),is\_end_j\}, j=1,2.,,,m$，每个样本被采样的概率基于$P(j) = \frac{p_j}{\sum\limits_i(p_i)}$，损失函数权重$w_j = (N*P(j))^{-\beta}/\max_i(w_i)$，计算当前目标Q值$y_j$：$$y_j= \begin{cases} R_j& {is\_end_j\; is \;true}\\ R_j + \gamma Q'(\phi(S'_j),\arg\max_{a'}Q(\phi(S'_j),a,w),w')& {is\_end_j\; is \;false} \end{cases}$$

　　　　　　g) 使用均方差损失函数$\frac{1}{m}\sum\limits_{j=1}^mw_j(y_j-Q(\phi(S_j),A_j,w))^2$，通过神经网络的梯度反向传播来更新Q网络的所有参数$w$

　　　　　　h) 重新计算所有样本的TD误差$\delta_j = y_j- Q(\phi(S_j),A_j,w)$，更新SumTree中所有节点的优先级$p_j = |\delta_j|$

　　　　　　i) 如果T%C=1,则更新目标Q网络参数$w'=w$

　　　　　　j) 如果$S'$是终止状态，当前轮迭代完毕，否则转到步骤b)

　　　　　　注意，上述第二步的f步和g步的Q值计算也都需要通过Q网络计算得到。另外，实际应用中，为了算法较好的收敛，探索率$\epsilon$需要随着迭代的进行而变小。

4. Prioritized Replay DDQN算法流程

　　　　下面我们给出Prioritized Replay DDQN算法的实例代码。仍然使用了OpenAI Gym中的CartPole-v0游戏来作为我们算法应用。CartPole-v0游戏的介绍参见这里。它比较简单，基本要求就是控制下面的cart移动使连接在上面的pole保持垂直不倒。这个任务只有两个离散动作，要么向左用力，要么向右用力。而state状态就是这个cart的位置和速度， pole的角度和角速度，4维的特征。坚持到200分的奖励则为过关。

　　　　完整的代码参见我的github: https://github.com/ljpzzz/machinelearning/blob/master/reinforcement-learning/ddqn_prioritised_replay.py，代码中的SumTree的结构和经验回放池的结构参考了morvanzhou的github代码。

　　　　这里重点讲下和第三节中算法描述不同的地方，主要是$w_j$的计算。注意到：$$w_j = \frac{ (N*P(j))^{-\beta}}{\max_i(w_i)} = \frac{ (N*P(j))^{-\beta}}{\max_i((N*P(i))^{-\beta})} = \frac{ (P(j))^{-\beta}}{\max_i((P(i))^{-\beta})} =( \frac{p_j}{\min_iP(i)})^{-\beta}$$

　　　　因此代码里面$w_j$，即ISWeights的计算代码是这样的：

def sample(self, n):
        b_idx, b_memory, ISWeights = np.empty((n,), dtype=np.int32), np.empty((n, self.tree.data[0].size)), np.empty((n, 1))
        pri_seg = self.tree.total_p / n       # priority segment
        self.beta = np.min([1., self.beta + self.beta_increment_per_sampling])  # max = 1

        min_prob = np.min(self.tree.tree[-self.tree.capacity:]) / self.tree.total_p     # for later calculate ISweight
        if min_prob == 0:
            min_prob = 0.00001
        for i in range(n):
            a, b = pri_seg * i, pri_seg * (i + 1)
            v = np.random.uniform(a, b)
            idx, p, data = self.tree.get_leaf(v)
            prob = p / self.tree.total_p
            ISWeights[i, 0] = np.power(prob/min_prob, -self.beta)
            b_idx[i], b_memory[i, :] = idx, data
        return b_idx, b_memory, ISWeights

　　　　上述代码的采样在第二节已经讲到。根据树的优先级的和total_p和采样数n，将要采样的区间划分为n段，每段来进行均匀采样，根据采样到的值落到的区间，决定被采样到的叶子节点。当我们拿到第i段的均匀采样值v以后，就可以去SumTree中找对应的叶子节点拿样本数据，样本叶子节点序号以及样本优先级了。代码如下：

def get_leaf(self, v):
        """
        Tree structure and array storage:
        Tree index:
             0         -> storing priority sum
            / \
          1     2
         / \   / \
        3   4 5   6    -> storing priority for transitions
        Array type for storing:
        [0,1,2,3,4,5,6]
        """
        parent_idx = 0
        while True:     # the while loop is faster than the method in the reference code
            cl_idx = 2 * parent_idx + 1         # this leaf's left and right kids
            cr_idx = cl_idx + 1
            if cl_idx >= len(self.tree):        # reach bottom, end search
                leaf_idx = parent_idx
                break
            else:       # downward search, always search for a higher priority node
                if v <= self.tree[cl_idx]:
                    parent_idx = cl_idx
                else:
                    v -= self.tree[cl_idx]
                    parent_idx = cr_idx

        data_idx = leaf_idx - self.capacity + 1
        return leaf_idx, self.tree[leaf_idx], self.data[data_idx]

　　　　除了采样部分，要注意的就是当梯度更新完毕后，我们要去更新SumTree的权重，代码如下，注意叶子节点的权重更新后，要向上回溯，更新所有祖先节点的权重。

self.memory.batch_update(tree_idx, abs_errors)  # update priority

def batch_update(self, tree_idx, abs_errors):
        abs_errors += self.epsilon  # convert to abs and avoid 0
        clipped_errors = np.minimum(abs_errors, self.abs_err_upper)
        ps = np.power(clipped_errors, self.alpha)
        for ti, p in zip(tree_idx, ps):
            self.tree.update(ti, p)

def update(self, tree_idx, p):
        change = p - self.tree[tree_idx]
        self.tree[tree_idx] = p
        # then propagate the change through tree
        while tree_idx != 0:    # this method is faster than the recursive loop in the reference code
            tree_idx = (tree_idx - 1) // 2
            self.tree[tree_idx] += change

　　　　除了上面这部分的区别，和DDQN比，TensorFlow的网络结构流程中多了一个TD误差的计算节点，以及损失函数多了一个ISWeights系数。此外，区别不大。