目录
1、0-1分布(两点分布、伯努利分布)
2、几何分布
3、二项分布
4、高斯分布(正态分布)
5、卡方分布
 (chi-square distribution)
(chi-square distribution) 6、t分布
单个二值型离散随机变量的分布,概率分布函数:
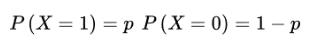
2、几何分布
离散型概率分布,定义为:n次伯努利试验中,试验k次才能得到一次成功的机率。即前k-1次皆失败,第k次成功的概率。
概率分布函数:
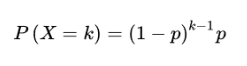
 3、二项分布
3、二项分布
n次伯努利试验,各次试验之间相互独立,每次试验只有两种可能(抛硬币),相互对立。设事件发生的概率是P,不发生的概率是1-P,n次重复独立试验中发生K次的概率:
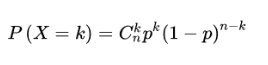
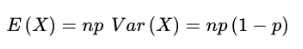
4、高斯分布(正态分布)
随机变量X服从数学期望为μ,方差为σ2的正态分布,记为N(μ,σ2)。
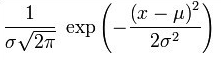
μ决定正态分布的位置。
标准差决定正态分布的幅度。

性质:

标准正态分布:μ=0,σ=1。
性质:
Φ(x)=1-Φ(-x)
![]()

5、卡方分布
 (chi-square distribution)
(chi-square distribution) 若n个相互独立的随机变量ξ₁,ξ₂,...,ξn ,均服从标准正态分布N(0,1)(也称独立同分布于标准正态分布),则这n个服从标准正态分布的随机变量的平方和构成一新的随机变量,其分布规律称为卡方分布(chi-square distribution)。
随机变量 :

记为:

其中参数
称为自由度,自由度不同就是另一个
分布。
卡方分布是由正态分布构造而成的一个新的分布,当自由度
 很大时,
很大时,  分布近似为正态分布。
分布近似为正态分布。 性质:

6、t分布
正态分布是许多统计方法的理论基础。μ和σ决定了正态分布的位置和形态。为了应用方便,常将一般的正太变量X通过u变换[(X-μ)/σ]转化成标准正态分布N(0,1),使原来各种形态的正态分布都转换成了μ=0,σ=1的标准正态分布,也称为u分布 。
根据中心极限定理,通过抽样模拟试验表明,在正态分布总体以固定n抽取若干个样本时,样本均数的分布仍然服从正态分布N(μ,
 )。所以对样本均数(均值)的分布进行u变换,也可以变换为标准正态分布。
)。所以对样本均数(均值)的分布进行u变换,也可以变换为标准正态分布。 实际工作中,σ2(总体方差)是未知的,所以常用s作为σ的估计值,为了与u变换区别,称为t变换。
统计量t值的分布称为t分布。假设随机变量X服从标准正态分布N(0,1),Y服从
 分布,那么
分布,那么  的分布称为自由度为n的t分布,记为
的分布称为自由度为n的t分布,记为 
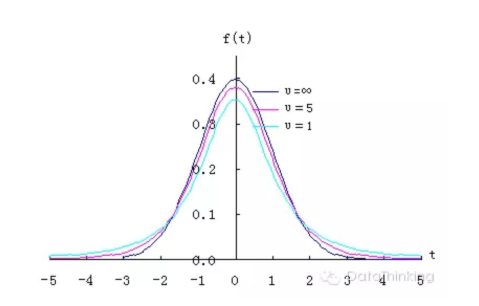
可以看出t分布以0为中心,左右对称的单峰分布;
t分布式一簇曲线,形态变化与n(确切的说自由度v)大小有关,自由度越小,t分布越低平;自由度越大,t分布曲线越接近标准正态分布(u分布)。
6.1 置信区间
已知X~N(μ,1)找一个区间,使得包含μ的真值的概率为95%,假n=5,则:
![]() ~ N(μ,
~ N(μ,
 ) ~ N(μ,1/5)
) ~ N(μ,1/5) 
α = 1 - 95% = 0.05
查表得:![]()
查表的方法:直接在标准正态分布表里面找概率 = 1-α/2 时的 z 取值。
含义:正态分布左侧的面积(概率)为0.975时候的横坐标值。(上分位)
Z1-α/2:是下分位表示,意思是右侧面积为0.975。
注意:置信区间双侧检验,所以要α/2.
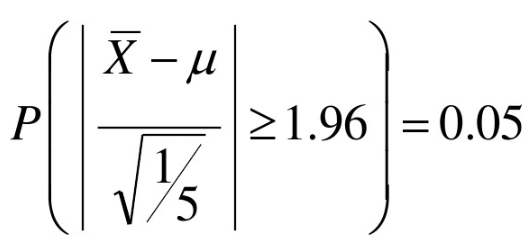
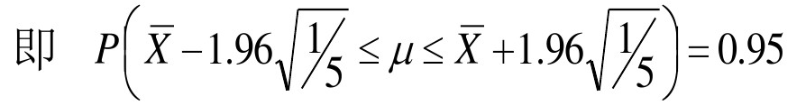
称随机区间![]() 为参数μ的置信度为95%的置信区间。
为参数μ的置信度为95%的置信区间。
(1)已知总体方差,求总体均值的置信区间

是总体样本均值;
α是显著水平(1-置信度),若置信度是95%,则α=1-0.95=0.05;
Zα/2称为Z值,可以查找标准正态分布表得到;(z(a/2)指的是标准正态分布的双侧临界值,z(a)当然就是单侧临界值)σ:总体的标准差;
n:抽样出来的样本个数;
:样本的标准误差
(2)未知总体方差,求总体均值μ的置信区间
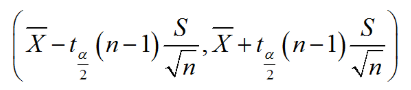
tα/2(n-1)称为t值,通过查t分布表得到(tα/2(n-1) = t1-α/2(n-1));
S:样本的标准差
:样本的平均误差
 称为
称为 分布。
分布。 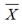 是总体样本均值;
是总体样本均值;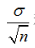 :样本的标准误差
:样本的标准误差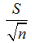 :样本的平均误差
:样本的平均误差