2020 牛客多校7 C A National Pandemic(树链剖分)

题意

有\(T\)组样例，第二行给\(n\),\(m\)，分别为点的个数和询问个数，接下来\(n-1\)行为边，之后是\(m\)行询问
询问有三种，\(1\) \(x\) \(w\), 表示点\(x\)增加\(w\)，其他所有点增减\(w-dis(x,y)\)(点\(y\)树上到\(x\)的距离)
\(2\) \(x\)，表示将点\(x\)的权值变为\(min(F(x), 0)\)
\(3\) \(x\)，表示询问\(x\)的权值\(F(x)\)

解法

对整颗树进行树链剖分（对各点做标记的部分只有两个dfs而已，不是很难），之后将重新标号的点映射到线段树上，并用线段树维护每个点的权值（除了2操作可以使用另外一个数组来维护每个点被减去的权值），操作1我们只需要维护一个全局变量，然后对x到根上所有的点的点权全部+2，这样我们就可以假装所有的1操作都是在根上操作的了~~(￣▽￣)／~~。最后计算结果时的式子为\(addw[x] - 1ll * cnt1 * dep[x] + golbal_wt + queryPath(1, x)\) 就是\(2\)操作的修改值 \(-\) 之前\(1\)操作的次数 \(*\) \(x\)的深度 \(+\) 全局权值 \(+\) 树上\(1\)到\(x\)的点权

先拿例题中的图举例
首先将树剖成三条链

经过操作\(1\) \(1\) \(5\)之后，全局变量变为\(4\),\(1\)的点权变为\(2\)，又经过\(2\) \(1\), \(1\)的点权修正值为\(-5\)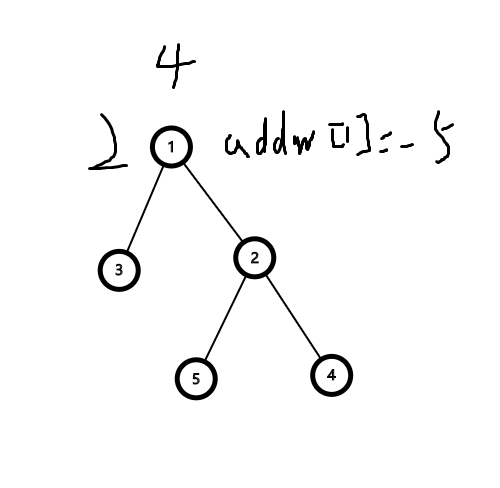

再经过\(1\) \(2\) \(7\)之后，\(1\), \(2\)的点权继续加\(2\)，全局变量\(+ 5 = 9\)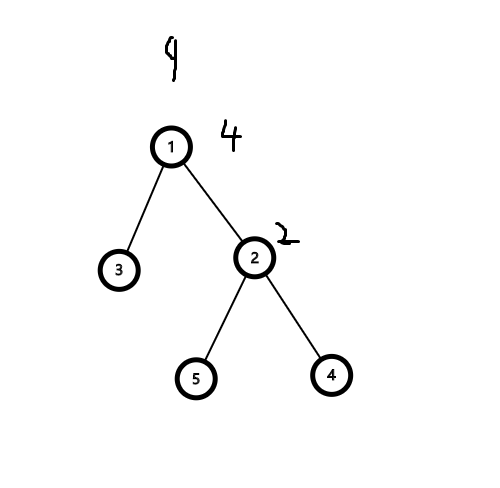

这样操作的时候，比如你要求点\(3\)的值，就是\(全局权重-dep[3] * 2 + queryPath(1,3) = 9\), 因为有两次操作\(1\)，而权值公式为\(w-dis(x,y)\)，所以减去两次\(dep[3]\),最后我们补上多减的值就是了。

又比如我们询问\(2\), 权值如上计算是\(11\)，按照最基本的式子原本应该是\(全局权重-cnt1*dep[2]\)，而因为\(1\),\(2\)都曾进行过一次操作，我们应该将操作点移到根后点\(2\)失去的贡献加回来,也就是每经过一个点，我们就将权重\(+2\)

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N = 5e4 + 7;

int t;
int n, m, u, v, op, w;
int head[N], cnte = 0, idx = 0;
int dep[N], dfn[N], fa[N], top[N], wson[N], siz[N], id[N];
ll addw[N], global_wt;


struct Edge{
    int to, nxt, val;
} edge[N << 1];
void addedge(int u, int v)
{
    edge[++cnte].nxt = head[u];
    edge[cnte].to = v;
    edge[cnte].val = 0;
    head[u] = cnte;
}

struct segment_tree
{
    #define lson rt << 1
    #define rson rt << 1 | 1

    ll sum[N << 2], add[N << 2];

    void udp(int rt, ll v, int l, int r)
    {
        sum[rt] += (r - l + 1ll) * v;
        add[rt] += v;
    }
    void build(int l, int r, int rt)
    {
        sum[rt] = add[rt] = 0;

        if (l == r) return;
        int mid = (l + r) >> 1;
        build(l, mid, lson);
        build(mid + 1, r, rson);
    }
    void push_down(int rt, int l, int r)
    {
        if(add[rt])
        {
            int mid = (l + r) >> 1;
            udp(lson, add[rt], l, mid);
            udp(rson, add[rt], mid + 1, r);
            add[rt] = 0;
        }
    }
    void update(int L, int R, ll c, int l, int r, int rt)
    {
        if (L == l && r == R )
        {
            udp(rt, c, l, r);
            return;
        }
        int mid = (l + r) >> 1;
        push_down(rt, l, r);

        if (L <= mid) update(L, min(R,mid), c, l, mid, lson);
        if (R > mid) update(max(L,mid + 1), R, c, mid + 1, r, rson);
        sum[rt] = sum[lson] + sum[rson];
    }
    ll query(int L, int R, int l, int r, int rt)
    {
        if (L == l && r == R) return sum[rt];
        int mid = (l + r) >> 1;
        push_down(rt, l, r);
        ll res = 0;
        if (R <= mid) res += query(L, R, l, mid, lson);
        else if (L > mid) res += query(L, R, mid + 1, r, rson);
        else return query(L, mid, l, mid, lson) + query(mid + 1, R, mid + 1, r, rson);
    }
} tree;

void init()
{
    cnte = 0;
    idx = 0;
    global_wt = 0;
    fill(head, head + N, 0);
    fill(fa, fa + N, 0);
    fill(siz, siz + N, 0);
    fill(wson, wson + N, 0);
    fill(addw, addw + N, 0);

}

void dfs1(int u)
{
    siz[u] = 1;
    for (int i = head[u]; i;i = edge[i].nxt)
    {
        int v = edge[i].to;
        if(v == fa[u]) continue;
        fa[v] = u;
        dep[v] = dep[u] + 1;
        dfs1(v);
        siz[u] += siz[v];
        if(siz[v] > siz[wson[u]]) wson[u] = v;
    }
}

void dfs2(int u, int chain)
{
    id[u] = ++idx, dfn[idx] = u;
    top[u] = chain;

    if(wson[u] != 0) dfs2(wson[u], chain);
    for (int i = head[u]; i; i = edge[i].nxt)
    {
        int v = edge[i].to;
        if(v == fa[u] || v == wson[u]) continue;
        dfs2(v, v);
    }
}

void udpPath(int u, int v, int val)
{
    while(top[u] != top[v])
    {
        if(dep[top[u]] < dep[top[v]]) swap(u, v);
        tree.update(id[top[u]], id[u], val, 1, n, 1);
        u = fa[top[u]];
    }
    if(dep[u] < dep[v]) swap(u, v);
    tree.update(id[v], id[u], val, 1, n, 1);
}


ll queryPath(int u, int v)
{
    ll res = 0;
    while(top[u] != top[v])
    {
        if(dep[top[u]] < dep[top[v]]) swap(u, v);
        res += tree.query(id[top[u]], id[u], 1, n, 1);
        u = fa[top[u]];
    }
    if(dep[u] < dep[v]) swap(u, v);
    res += tree.query(id[v], id[u], 1, n, 1);
    return res;
}



void solve()
{
    scanf("%d %d", &n, &m);
    for (int i = 1; i < n; i++)
    {
        scanf("%d %d", &u, &v);
        addedge(u, v);
        addedge(v, u);
    }
    tree.build(1, n, 1);
    dep[1] = 1;
    dfs1(1);
    dfs2(1, 1);
    int cnt1 = 0;
    while(m--)
    {
        scanf("%d", &op);
        if(op == 1)
        {
            scanf("%d %d", &u, &w);
            global_wt += w;
            global_wt -= dep[u];
            cnt1++;
            udpPath(1, u, 2);
        }
        else if(op == 2)
        {
            scanf("%d", &u);
            ll weight = addw[u] - 1ll * cnt1 * dep[u] + global_wt + queryPath(1, u);
            if(weight > 0) addw[u] -= weight;
        }
        else
        {
            scanf("%d", &u);
            ll weight = addw[u] - 1ll * cnt1 * dep[u] + global_wt + queryPath(1, u);
            printf("%lld\n", weight);
        }
        
    }
}

int main()
{
    scanf("%d", &t);
    while(t--)
    {       
        init();
        solve();
    }
    return 0;
}

来源：oschina

链接：https://my.oschina.net/u/4303535/blog/4464029

标签

QueryPath