[TOC]
2019.1.27
#10082. 「一本通 3.3 例 1」Word Rings
题意
每组数据读入一个n和n个字符串。定义前2个与末尾2个字母相同可以连接。问使这个环串的平均长度最大。求这个最大值。不存在输出$No solution$。
思路
平均值公式: $$ Average=(E_1+E_2+.....+E_n)/n $$
$$ Average*n=(E_1+E_2+...+E_n) $$
$$ (E_1-Average)+(E_2-Average)+...+(E_n-Average)=0 $$
那么可以二分答案: $$ (E_1-Ans)+(E_2-Ans)+...+(E_n-Ans)\geq0 $$ 然后瞎搞spfa。
#include<algorithm>
#include<bitset>
#include<complex>
#include<deque>
#include<exception>
#include<fstream>
#include<functional>
#include<iomanip>
#include<ios>
#include<iosfwd>
#include<iostream>
#include<istream>
#include<iterator>
#include<limits>
#include<list>
#include<locale>
#include<map>
#include<memory>
#include<new>
#include<numeric>
#include<ostream>
#include<queue>
#include<set>
#include<sstream>
#include<stack>
#include<stdexcept>
#include<streambuf>
#include<string>
#include<typeinfo>
#include<utility>
#include<valarray>
#include<vector>
#include<cctype>
#include<cerrno>
#include<cfloat>
#include<ciso646>
#include<climits>
#include<clocale>
#include<cmath>
#include<csetjmp>
#include<csignal>
#include<cstdarg>
#include<cstddef>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<ctime>
#define E 200010
#define eps 1e-3
using namespace std;
inline int read(){
int res=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9') res=res*10+ch-'0',ch=getchar();
return res*f;
}
inline void write(int x){
if(x<0) putchar('-'),x=-x;
if(x<10) putchar(x+'0');
else{
write(x/10);
putchar(x%10+'0');
}
}
//queue<int> q;
//set<int> s;
//priority_queue<int> q1;
//priority_queue<int,vector<int>,greater<int> > q2;
//list<int> l;
//stack<int> s;
int n;
string str[100010];
int fir[E],nxt[E],son[E],tot,cnt,Max;
double w[E],dis[E],flag;
int vis[E];
int f[6666];
void add(int x,int y,double z){++tot;son[tot]=y;nxt[tot]=fir[x];fir[x]=tot;w[tot]=z;}
void spfa(int s,int v,double mid){
if(flag==1) return ;
vis[s]=v;
for(int i=fir[s];i;i=nxt[i]){
int to=son[i];
if(dis[s]+w[i]>dis[to]+mid){
dis[to]=dis[s]+w[i]-mid;
if(dis[to]>Max){
flag=1;
return ;
}
if(!vis[to]) spfa(to,v,mid);
if(flag) return ;
else if(vis[to]==v){
flag=1;
return ;
}
}
}
vis[s]=0;
}
bool check(double mid){
flag=0;
for(int i=0;i<=cnt;i++) dis[i]=0.0;
memset(vis,0,sizeof(vis));
for(int i=1;i<=cnt;i++){
spfa(i,i,mid);
if(flag==1) break;
}
return flag;
}
int main(){
// freopen("code.in","r",stdin);freopen("code.out","w",stdout);
n=read();
while(n!=0){
for(int i=1;i<=n;i++) cin>>str[i];
memset(fir,0,sizeof(fir));
memset(f,0,sizeof(f));
tot=0;cnt=0;Max=0;
for(int i=1;i<=n;i++){
int len=str[i].length();
Max=max(Max,len);
int a=(str[i][0]-'a')*26+str[i][1]-'a';
int b=(str[i][len-2]-'a')*26+str[i][len-1]-'a';
if(!f[a]) f[a]=++cnt;
int A=f[a];
if(!f[b]) f[b]=++cnt;
int B=f[b];
add(A,B,(double)len);
}
Max*=n;
double l=0,r=1000,ans=-1,mid;
while(l+eps<r){
mid=(l+r)/2;
if(check(mid)) l=mid,ans=mid;
else r=mid;
}
if(ans!=-1) printf("%.2lf\n",ans);
else puts("No solution");
n=read();
}
return 0;
}
#10083. 「一本通 3.3 例 2」双调路径
题意
读入一个图,计算最小路径的总数。费用时间都相同的两条最小路径只算一条,输出不同种类的最小路径数。
思路
设$$f[i][j]$$表示在i点且已花费j时的最少时间 $$ f[i][j]=Min(f[k][i-Cost(k,i)]+Time(k,i)|For Each Edge(k,i)) $$
#include<algorithm>
#include<bitset>
#include<complex>
#include<deque>
#include<exception>
#include<fstream>
#include<functional>
#include<iomanip>
#include<ios>
#include<iosfwd>
#include<iostream>
#include<istream>
#include<iterator>
#include<limits>
#include<list>
#include<locale>
#include<map>
#include<memory>
#include<new>
#include<numeric>
#include<ostream>
#include<queue>
#include<set>
#include<sstream>
#include<stack>
#include<stdexcept>
#include<streambuf>
#include<string>
#include<typeinfo>
#include<utility>
#include<valarray>
#include<vector>
#include<cctype>
#include<cerrno>
#include<cfloat>
#include<ciso646>
#include<climits>
#include<clocale>
#include<cmath>
#include<csetjmp>
#include<csignal>
#include<cstdarg>
#include<cstddef>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<ctime>
#define E 5010
#define eps 1e-3
using namespace std;
inline int read(){
int res=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9') res=res*10+ch-'0',ch=getchar();
return res*f;
}
inline void write(int x){
if(x<0) putchar('-'),x=-x;
if(x<10) putchar(x+'0');
else{
write(x/10);
putchar(x%10+'0');
}
}
//queue<int> q;
//set<int> s;
//priority_queue<int> q1;
//priority_queue<int,vector<int>,greater<int> > q2;
//list<int> l;
//stack<int> s;
int n,m,s,e;
int fir[E],nxt[E],son[E],w[E],cost[E],tot;
void add(int x,int y,int z,int t){++tot;w[tot]=z;son[tot]=y;nxt[tot]=fir[x];cost[tot]=t;fir[x]=tot;}
int dp[105][10005][3],Max,ans,Min=2e9;
int vis[105][10005];
struct node{int pos,dis;};
queue<node> q;
node make(int x,int y){node pp;pp.pos=x;pp.dis=y;return pp;}
void spfa(){
while(!q.empty()) q.pop();
for(int i=1;i<=n;i++){
for(int j=0;j<=10005;j++){
dp[i][j][0]=2e9;
dp[i][j][1]=0;
}
}
dp[s][0][0]=0;
dp[s][0][1]=1;
vis[s][0]=1;
q.push(make(s,0));
while(!q.empty()){
int u=q.front().pos,dis=q.front().dis;q.pop();
vis[u][dis]=0;
for(int i=fir[u];i;i=nxt[i]){
int to=son[i];
if(dis+w[i]>Max+1) continue ;
if(dp[u][dis][0]+cost[i]<dp[to][dis+w[i]][0]){
dp[to][dis+w[i]][0]=dp[u][dis][0]+cost[i];
dp[to][dis+w[i]][1]=1;
if(vis[to][dis+w[i]]==0){
vis[to][dis+w[i]]=1;
q.push(make(to,dis+w[i]));
}
}
}
}
}
int main(){
// freopen("code.in","r",stdin);freopen("code.out","w",stdout);
n=read();m=read();s=read();e=read();
for(int i=1;i<=m;i++){
int x=read(),y=read(),z=read(),t=read();
add(x,y,z,t);
add(y,x,z,t);
}
Max=(n-1)*100+5;
spfa();
for(int i=0;i<=Max;i++){
if(!dp[e][i][1]) continue ;
if(dp[e][i][0]<Min){
ans++;
Min=dp[e][i][0];
}
}
write(ans);putchar('\n');
return 0;
}
#10084. 「一本通 3.3 练习 1」最小圈
题意
读入一个有向图,求图中最小环的最小平均值时多少。
思路
当然食用二分+spfa啦。
基本思路同#10082. 「一本通 3.3 例 1」Word Rings
平均值公式: $$ Average=(E_1+E_2+.....+E_n)/n $$
$$ Average*n=(E_1+E_2+...+E_n) $$
$$ (E_1-Average)+(E_2-Average)+...+(E_n-Average)=0 $$
那么可以二分答案: $$ (E_1-Ans)+(E_2-Ans)+...+(E_n-Ans)\geq0 $$ 然后瞎搞spfa。
但这次求最小值。
改一改符号就好了。
#include<algorithm>
#include<bitset>
#include<complex>
#include<deque>
#include<exception>
#include<fstream>
#include<functional>
#include<iomanip>
#include<ios>
#include<iosfwd>
#include<iostream>
#include<istream>
#include<iterator>
#include<limits>
#include<list>
#include<locale>
#include<map>
#include<memory>
#include<new>
#include<numeric>
#include<ostream>
#include<queue>
#include<set>
#include<sstream>
#include<stack>
#include<stdexcept>
#include<streambuf>
#include<string>
#include<typeinfo>
#include<utility>
#include<valarray>
#include<vector>
#include<cctype>
#include<cerrno>
#include<cfloat>
#include<ciso646>
#include<climits>
#include<clocale>
#include<cmath>
#include<csetjmp>
#include<csignal>
#include<cstdarg>
#include<cstddef>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<ctime>
#define E 20010
#define eps 1e-10
using namespace std;
inline int read(){
int res=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9') res=res*10+ch-'0',ch=getchar();
return res*f;
}
inline void write(int x){
if(x<0) putchar('-'),x=-x;
if(x<10) putchar(x+'0');
else{
write(x/10);
putchar(x%10+'0');
}
}
//queue<int> q;
//set<int> s;
//priority_queue<int> q1;
//priority_queue<int,vector<int>,greater<int> > q2;
//list<int> l;
//stack<int> s;
int n,m;
int fir[E],nxt[E],son[E],tot;
double w[E],Max;
void add(int x,int y,double z){++tot;nxt[tot]=fir[x];son[tot]=y;fir[x]=tot;w[tot]=z;}
double dis[E],flag;
int vis[E];
int spfa(int s,double mid){
vis[s]=1;
for(int i=fir[s];i;i=nxt[i]){
int to=son[i];
if(dis[s]+w[i]-mid<dis[to]){
dis[to]=dis[s]+w[i]-mid;
if(vis[to]||spfa(to,mid)){vis[s]=0;return 1;}
}
}
vis[s]=0;
return 0;
}
bool check(double mid){
for(int i=0;i<=n;i++) dis[i]=0.0;
memset(vis,0,sizeof(vis));
for(int i=1;i<=n;i++){
if(spfa(i,mid)==1) return 1;
}
return 0;
}
int main(){
n=read();m=read();
for(int i=1;i<=m;i++){
int x=read(),y=read();double z;
cin>>z;
add(x,y,(double)z);
}
double l=-1e7,r=1e7,mid,ans;
while(l+eps<r){
mid=(l+r)/2;
if(check(mid)) r=mid-eps,ans=mid;
else l=mid+eps;
}
printf("%.8lf\n",ans);
return 0;
}
#10085. 「一本通 3.3 练习 2」虫洞 Wormholes
题意
现在 John 想借助这些虫洞来回到过去(在出发时刻之前回到出发点),请你告诉他能办到吗。 John 将向你提供 F 个农场的地图。
思路
当然食用spfa啦。
当然,因为我懒,所以将上一题代码改一改就好了呀。
注意建双向边。
注意建负边。
check时只需要传入参数0就好了。
因为又没有让你求平均值QWQ
#include<algorithm>
#include<bitset>
#include<complex>
#include<deque>
#include<exception>
#include<fstream>
#include<functional>
#include<iomanip>
#include<ios>
#include<iosfwd>
#include<iostream>
#include<istream>
#include<iterator>
#include<limits>
#include<list>
#include<locale>
#include<map>
#include<memory>
#include<new>
#include<numeric>
#include<ostream>
#include<queue>
#include<set>
#include<sstream>
#include<stack>
#include<stdexcept>
#include<streambuf>
#include<string>
#include<typeinfo>
#include<utility>
#include<valarray>
#include<vector>
#include<cctype>
#include<cerrno>
#include<cfloat>
#include<ciso646>
#include<climits>
#include<clocale>
#include<cmath>
#include<csetjmp>
#include<csignal>
#include<cstdarg>
#include<cstddef>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<ctime>
#define E 20010
#define eps 1e-10
using namespace std;
inline int read(){
int res=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9') res=res*10+ch-'0',ch=getchar();
return res*f;
}
inline void write(int x){
if(x<0) putchar('-'),x=-x;
if(x<10) putchar(x+'0');
else{
write(x/10);
putchar(x%10+'0');
}
}
//queue<int> q;
//set<int> s;
//priority_queue<int> q1;
//priority_queue<int,vector<int>,greater<int> > q2;
//list<int> l;
//stack<int> s;
int n,m;
int fir[E],nxt[E],son[E],tot;
double w[E],Max;
void add(int x,int y,double z){++tot;nxt[tot]=fir[x];son[tot]=y;fir[x]=tot;w[tot]=z;}
double dis[E],flag;
int vis[E];
int spfa(int s,double mid){
vis[s]=1;
for(int i=fir[s];i;i=nxt[i]){
int to=son[i];
if(dis[s]+w[i]-mid<dis[to]){
dis[to]=dis[s]+w[i]-mid;
if(vis[to]||spfa(to,mid)){vis[s]=0;return 1;}
}
}
vis[s]=0;
return 0;
}
bool check(double mid){
for(int i=0;i<=n;i++) dis[i]=0.0;
memset(vis,0,sizeof(vis));
for(int i=1;i<=n;i++){
if(spfa(i,mid)==1) return 1;
}
return 0;
}
int main(){
int T,W;
T=read();
while(T--){
n=read();m=read();W=read();
tot=0;
memset(fir,0,sizeof(fir));
for(int i=1;i<=m;i++){
int x=read(),y=read();double z;
cin>>z;
add(x,y,(double)z);
add(y,x,(double)z);
}
for(int i=1;i<=W;i++){
int x=read(),y=read();double z;
cin>>z;
add(x,y,-z);
}
if(check(0)) puts("YES");
else puts("NO");
}
return 0;
}
#10086. 「一本通 3.3 练习 3」Easy SSSP
题意
给你一个图,问从源点到每个节点的最短路径分别是多少。
如果存在负权回路,只输出一行 -1;如果不存在负权回路,再求出一个点 S 到每个点的最短路的长度。如果 S 与这个点不连通,则输出 NoPath。
思路
当然食用spfa啦。
先跑一下非源点的。万一数据卡你其他有环呢?
然后再跑一次源点。得出Ans
#include<algorithm>
#include<bitset>
#include<complex>
#include<deque>
#include<exception>
#include<fstream>
#include<functional>
#include<iomanip>
#include<ios>
#include<iosfwd>
#include<iostream>
#include<istream>
#include<iterator>
#include<limits>
#include<list>
#include<locale>
#include<map>
#include<memory>
#include<new>
#include<numeric>
#include<ostream>
#include<queue>
#include<set>
#include<sstream>
#include<stack>
#include<stdexcept>
#include<streambuf>
#include<string>
#include<typeinfo>
#include<utility>
#include<valarray>
#include<vector>
#include<cctype>
#include<cerrno>
#include<cfloat>
#include<ciso646>
#include<climits>
#include<clocale>
#include<cmath>
#include<csetjmp>
#include<csignal>
#include<cstdarg>
#include<cstddef>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<ctime>
#define E 2000010
#define eps 1e-10
#define ll long long
using namespace std;
inline ll read(){
ll res=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9') res=res*10+ch-'0',ch=getchar();
return res*f;
}
inline void write(ll x){
if(x<0) putchar('-'),x=-x;
if(x<10) putchar(x+'0');
else{
write(x/10);
putchar(x%10+'0');
}
}
//queue<ll> q;
//set<ll> s;
//priority_queue<ll> q1;
//priority_queue<ll,vector<ll>,greater<ll> > q2;
//list<ll> l;
//stack<ll> s;
ll n,m;
ll fir[E],nxt[E],son[E],tot;
double w[E],Max;
void add(ll x,ll y,double z){++tot;nxt[tot]=fir[x];son[tot]=y;fir[x]=tot;w[tot]=z;}
double dis[E],flag;
ll vis[E];
queue<int> q;
int tt[E];
ll spfa(ll s){
vis[s]=1;
q.push(s);
while(!q.empty()){
int u=q.front();q.pop();
for(ll i=fir[u];i;i=nxt[i]){
ll to=son[i];
if(dis[u]+w[i]<dis[to]){
dis[to]=dis[u]+w[i];
tt[to]++;
if(tt[to]>n+1){
puts("-1");
exit(0);
}
if(vis[to]==0){
vis[to]=1;
q.push(to);
}
}
}
vis[u]=0;
}
return 0;
}
ll st[E];
int main(){
ll T=1,S;
while(T--){
n=read();m=read();S=read();
tot=0;
memset(fir,0,sizeof(fir));
for(ll i=1;i<=m;i++){
ll x=read(),y=read();double z;
cin>>z;
add(x,y,(double)z);
}
for(ll i=0;i<=n;i++) dis[i]=2e18;
dis[S]=0;
memset(vis,0,sizeof(vis));
spfa(2);
for(ll i=0;i<=n;i++) dis[i]=2e18;
dis[S]=0;
memset(vis,0,sizeof(vis));
spfa(S);
for(ll i=1;i<=n;i++){
if(i==S) puts("0");
else if(dis[i]>=2e18) puts("NoPath");
else{
printf("%.0lf\n",dis[i]);
}
}
}
return 0;
}
#10087. 「一本通 3.4 例 1」Intervals
题意
从$0\sim 5\times 10^4$中选出尽量少的整数,使每个区间$[a_i,b_i]$内都有至少$c_i$个数被选出。
思路
当然食用spfa啦。
设$s[k]$表示0~k中至少选多少个整数。根据题意可得: $$ s[b_i]-s[a_i-1]\geq c_i $$
$$ s[k]-s[k-1]\geq0 $$
$$ s[k]-s[k-1]\leq1 $$
也就是: $$ s[k-1]-s[k]\geq-1 $$ 那么跑一次最长路就好了。
#include<algorithm>
#include<bitset>
#include<complex>
#include<deque>
#include<exception>
#include<fstream>
#include<functional>
#include<iomanip>
#include<ios>
#include<iosfwd>
#include<iostream>
#include<istream>
#include<iterator>
#include<limits>
#include<list>
#include<locale>
#include<map>
#include<memory>
#include<new>
#include<numeric>
#include<ostream>
#include<queue>
#include<set>
#include<sstream>
#include<stack>
#include<stdexcept>
#include<streambuf>
#include<string>
#include<typeinfo>
#include<utility>
#include<valarray>
#include<vector>
#include<cctype>
#include<cerrno>
#include<cfloat>
#include<ciso646>
#include<climits>
#include<clocale>
#include<cmath>
#include<csetjmp>
#include<csignal>
#include<cstdarg>
#include<cstddef>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<ctime>
#define E 2000010
#define eps 1e-10
#define ll long long
using namespace std;
inline ll read(){
ll res=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9') res=res*10+ch-'0',ch=getchar();
return res*f;
}
inline void write(ll x){
if(x<0) putchar('-'),x=-x;
if(x<10) putchar(x+'0');
else{
write(x/10);
putchar(x%10+'0');
}
}
//queue<ll> q;
//set<ll> s;
//priority_queue<ll> q1;
//priority_queue<ll,vector<ll>,greater<ll> > q2;
//list<ll> l;
//stack<ll> s;
ll n,m;
ll fir[E],nxt[E],son[E],tot;
double w[E];
void add(ll x,ll y,double z){++tot;nxt[tot]=fir[x];son[tot]=y;fir[x]=tot;w[tot]=z;}
double dis[E],flag;
ll vis[E];
queue<int> q;
int tt[E];
ll spfa(ll s){
vis[s]=1;
q.push(s);
while(!q.empty()){
int u=q.front();q.pop();
for(ll i=fir[u];i;i=nxt[i]){
ll to=son[i];
if(dis[u]+w[i]>dis[to]){
dis[to]=dis[u]+w[i];
tt[to]++;
if(tt[to]>n+1){
puts("-1");
exit(0);
}
if(vis[to]==0){
vis[to]=1;
q.push(to);
}
}
}
vis[u]=0;
}
return 0;
}
ll st[E],Min,Max;
int main(){
n=read();
Max=-1;Min=2e9;
for(int i=1;i<=n;i++){
ll x=read(),y=read(),z=read();
add(x-1,y,z);
Max=max(Max,y);
Min=min(Min,x-1);
}
for(int i=Min;i<=Max;i++){
add(i,i+1,0);
add(i+1,i,-1);
}
for(int i=Min;i<=Max;i++) dis[i]=-2e9;
memset(vis,0,sizeof(vis));
dis[Min]=0;
spfa(Min);
printf("%.0lf\n",dis[Max]);
return 0;
}
#10088. 「一本通 3.4 例 2」出纳员问题
题意
$、、R(0)、R(1)、R(2)...R(23)$表示第x个时刻需要$R(x)$个出纳员,有n个出纳员申请工作,第$i$个出纳员从$t_i$时刻开始工作$8$小时,问至少需要多少出纳员?
思路
设$x[i]$表示第i时刻实际上需要雇佣$x[i]$人,$r[i]$为第i时刻至少需要$r[i]$个人。 $$ x[i-7]+x[i-6]+x[i-5]+x[i-4]+x[i-3]+x[i-2]+x[i-1]+x[i]\geq r[i] $$ 设$s[i]=x[1]+x[2]+x[3]+...+x[i]$,可得: $$ s[i]-s[i-1]\geq0 $$
$$ s[i-1]-s[i]\geq-num[i] $$
$$ s[i]-s[i-8]\geq r[i] $$
$$ s[i]-s[i+16]\geq r[i]-s[23] $$
#include<algorithm>
#include<bitset>
#include<complex>
#include<deque>
#include<exception>
#include<fstream>
#include<functional>
#include<iomanip>
#include<ios>
#include<iosfwd>
#include<iostream>
#include<istream>
#include<iterator>
#include<limits>
#include<list>
#include<locale>
#include<map>
#include<memory>
#include<new>
#include<numeric>
#include<ostream>
#include<queue>
#include<set>
#include<sstream>
#include<stack>
#include<stdexcept>
#include<streambuf>
#include<string>
#include<typeinfo>
#include<utility>
#include<valarray>
#include<vector>
#include<cctype>
#include<cerrno>
#include<cfloat>
#include<ciso646>
#include<climits>
#include<clocale>
#include<cmath>
#include<csetjmp>
#include<csignal>
#include<cstdarg>
#include<cstddef>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<ctime>
#define E 2000010
#define eps 1e-10
#define ll long long
using namespace std;
inline ll read(){
ll res=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9') res=res*10+ch-'0',ch=getchar();
return res*f;
}
inline void write(ll x){
if(x<0) putchar('-'),x=-x;
if(x<10) putchar(x+'0');
else{
write(x/10);
putchar(x%10+'0');
}
}
//queue<ll> q;
//set<ll> s;
//priority_queue<ll> q1;
//priority_queue<ll,vector<ll>,greater<ll> > q2;
//list<ll> l;
//stack<ll> s;
ll n,m;
ll fir[E],nxt[E],son[E],tot;
int w[E];
void add(ll x,ll y,ll z){++tot;nxt[tot]=fir[x];son[tot]=y;fir[x]=tot;w[tot]=z;}
int dis[E],flag;
ll vis[E];
queue<int> q;
int tt[E];
ll spfa(ll s){
memset(dis,63,sizeof(dis));
memset(tt,0,sizeof(tt));
memset(vis,0,sizeof(vis));
dis[24]=0;
vis[24]=1;
q.push(24);
while(!q.empty()){
int u=q.front();q.pop();
for(ll i=fir[u];i;i=nxt[i]){
ll to=son[i];
if(dis[u]+w[i]<dis[to]){
dis[to]=dis[u]+w[i];
tt[to]++;
if(tt[to]>n+1){
return 0;
}
if(vis[to]==0){
vis[to]=1;
q.push(to);
}
}
}
vis[u]=0;
}
return dis[0]==-s;
}
ll T,r[E],Min,Max,s[E],num[E];
void work(int x){
memset(fir,0,sizeof(fir));tot=0;
for(register int i=1;i<=24;i++) add(i,i-1,0),add(i-1,i,num[i]);
for(register int i=8;i<=24;i++) add(i,i-8,-r[i]);
for(register int j=1;j<=7;j++) add(j,j+16,x-r[j]);
add(24,0,-x);
}
int main(){
T=read();
while(T--){
for(int i=1;i<=24;i++){
r[i]=read();num[i]=0;
}
n=read();
for(int i=1;i<=n;i++){
int t=read();t++;
num[t]++;
}
int l=0,r=n,ans=2e9;
while(l<=r){
int mid=(l+r)/2;
work(mid);
if(spfa(mid)) ans=mid,r=mid-1;
else l=mid+1;
}
if(ans==2e9) puts("No Solution");
else write(ans),putchar('\n');
}
return 0;
}
#10089. 「一本通 3.4 练习 1」糖果
题意
满足条件:
如果 X=1.表示第 A 个小朋友分到的糖果必须和第 B 个小朋友分到的精果一样多。 如果 X=2,表示第 A 个小朋友分到的糖果必须少于第 B 个小朋友分到的糖果。 如果 X=3,表示第 A 个小朋友分到的糖果必须不少于第 B 个小朋友分到的糖果。 如果 X=4,表示第 A 个小朋友分到的糖果必须多于第 B 个小朋友分到的糖果。 如果 X=5,表示第 A 个小朋友分到的糖果必须不多于第 B 个小朋友分到的糖果。
求至少需要准备的糖果数?
思路
如果 X=1 $$ B=A $$ 如果 X=2 $$ B+1\ge A $$ 如果 X=3 $$ A\ge B $$ 如果 X=4 $$ A-1\ge B $$ 如果 X=5 $$ B \ge A $$ 那么就好了嘛:
#include<algorithm>
#include<bitset>
#include<complex>
#include<deque>
#include<exception>
#include<fstream>
#include<functional>
#include<iomanip>
#include<ios>
#include<iosfwd>
#include<iostream>
#include<istream>
#include<iterator>
#include<limits>
#include<list>
#include<locale>
#include<map>
#include<memory>
#include<new>
#include<numeric>
#include<ostream>
#include<queue>
#include<set>
#include<sstream>
#include<stack>
#include<stdexcept>
#include<streambuf>
#include<string>
#include<typeinfo>
#include<utility>
#include<valarray>
#include<vector>
#include<cctype>
#include<cerrno>
#include<cfloat>
#include<ciso646>
#include<climits>
#include<clocale>
#include<cmath>
#include<csetjmp>
#include<csignal>
#include<cstdarg>
#include<cstddef>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<ctime>
#define E 300010
#define eps 1e-10
#define ll long long
#pragma GCC optimize(2)
using namespace std;
inline ll read(){
ll res=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9') res=res*10+ch-'0',ch=getchar();
return res*f;
}
inline void write(ll x){
if(x<0) putchar('-'),x=-x;
if(x<10) putchar(x+'0');
else{
write(x/10);
putchar(x%10+'0');
}
}
//queue<ll> q;
//set<ll> s;
//priority_queue<ll> q1;
//priority_queue<ll,vector<ll>,greater<ll> > q2;
//list<ll> l;
//stack<ll> s;
ll n,k;
ll fir[E],nxt[E],son[E],w[E],tot,inf,ans;
inline void add(register ll x,register ll y,register ll z){
++tot;
w[tot]=z;
nxt[tot]=fir[x];
fir[x]=tot;
son[tot]=y;
}
ll dis[E],vis[E],tt[E];
deque<ll> q;
inline void spfa(){
memset(dis,0,sizeof(dis));
memset(tt,0,sizeof(tt));
memset(vis,0,sizeof(vis));inf=dis[0];
dis[0]=0;vis[0]=1;
while(!q.empty()) q.pop_front();
q.push_back(0);
while(!q.empty()){
register ll u=q.front();q.pop_front();
vis[u]=0;
for(register ll i=fir[u];i;i=nxt[i]){
register ll to=son[i];
if(dis[to]<dis[u]+w[i]){
tt[to]++;
dis[to]=dis[u]+w[i];
if(tt[to]>n+1){
puts("-1");
exit(0);
}
if(!vis[to]){
vis[to]=1;
if(!q.empty()&&dis[to]<dis[q.front()]) q.push_front(to);
else q.push_back(to);
}
}
}
}
}
int main(){
n=read();k=read();
for(register ll i=1;i<=k;i++){
ll x=read(),a=read(),b=read();
if(a==b&&(x==2||x==4)){
puts("-1");
return 0;
}
if(x==1) add(a,b,0),add(b,a,0);
if(x==2) add(a,b,1);
if(x==3) add(b,a,0);
if(x==4) add(b,a,1);
if(x==5) add(a,b,0);
}
for(register ll i=1;i<=n;i++) add(0,i,1);
spfa();
for(register ll i=1;i<=n;i++){
ans+=dis[i];
}
write(ans);putchar('\n');
return 0;
}
#10090. 「一本通 3.4 练习 2」布局 Layout
题意
有些奶牛是好基友,它们希望彼此之间的距离小于等于某个数。有些奶牛是情敌,它们希望彼此之间的距离大于等于某个数。
思路
如果两只奶牛是好基友,那么: $$ A-B\leq D $$ 如果两只奶牛是情敌,那么: $$ A-B\ge D $$ 即: $$ D\leq A-B $$ 也就是: $$ B-A\leq -D $$ 直接上代码:
#include<algorithm>
#include<bitset>
#include<complex>
#include<deque>
#include<exception>
#include<fstream>
#include<functional>
#include<iomanip>
#include<ios>
#include<iosfwd>
#include<iostream>
#include<istream>
#include<iterator>
#include<limits>
#include<list>
#include<locale>
#include<map>
#include<memory>
#include<new>
#include<numeric>
#include<ostream>
#include<queue>
#include<set>
#include<sstream>
#include<stack>
#include<stdexcept>
#include<streambuf>
#include<string>
#include<typeinfo>
#include<utility>
#include<valarray>
#include<vector>
#include<cctype>
#include<cerrno>
#include<cfloat>
#include<ciso646>
#include<climits>
#include<clocale>
#include<cmath>
#include<csetjmp>
#include<csignal>
#include<cstdarg>
#include<cstddef>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<ctime>
#define E 300010
#define eps 1e-10
#define ll long long
#pragma GCC optimize(2)
using namespace std;
inline ll read(){
ll res=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9') res=res*10+ch-'0',ch=getchar();
return res*f;
}
inline void write(ll x){
if(x<0) putchar('-'),x=-x;
if(x<10) putchar(x+'0');
else{
write(x/10);
putchar(x%10+'0');
}
}
//queue<ll> q;
//set<ll> s;
//priority_queue<ll> q1;
//priority_queue<ll,vector<ll>,greater<ll> > q2;
//list<ll> l;
//stack<ll> s;
ll n,k;
ll fir[E],nxt[E],son[E],w[E],tot,inf,ans;
inline void add(register ll x,register ll y,register ll z){
++tot;
w[tot]=z;
nxt[tot]=fir[x];
fir[x]=tot;
son[tot]=y;
}
ll dis[E],vis[E],tt[E];
deque<ll> q;
inline void spfa(int s){
memset(dis,63,sizeof(dis));
memset(tt,0,sizeof(tt));
memset(vis,0,sizeof(vis));inf=dis[0];
dis[s]=0;vis[s]=1;
while(!q.empty()) q.pop_front();
q.push_back(s);
while(!q.empty()){
register ll u=q.front();q.pop_front();
vis[u]=0;
for(register ll i=fir[u];i;i=nxt[i]){
register ll to=son[i];
if(dis[to]>dis[u]+w[i]){
tt[to]++;
dis[to]=dis[u]+w[i];
if(tt[to]>n+1){
puts("-1");
exit(0);
}
if(!vis[to]){
vis[to]=1;
if(!q.empty()&&dis[to]<dis[q.front()]) q.push_front(to);
else q.push_back(to);
}
}
}
}
}
int k1,k2;
int main(){
n=read();k1=read();k2=read();
for(register ll i=1;i<=k1;i++){
ll x=read(),y=read(),z=read();
add(x,y,z);
}
for(register ll i=1;i<=k2;i++){
ll x=read(),y=read(),z=read();
add(y,x,-z);
}
spfa(1);
ans=dis[n];
for(int i=1;i<=n;i++) spfa(i);
if(ans>=inf) puts("-2");
else write(ans),putchar('\n');
return 0;
}
#130. 树状数组 1 :单点修改,区间查询
题意
这是一道模板题。
给定Q个操作:
1 i x:给定 $i,x$,将 $a[i]$ 加上 $x$;2 l r:给定 $l,r$,求 $\sum_{i=l}^ra[i]$ 的值(换言之,求 $a[l]+a[l+1]+\dots+a[r]$ 的值)。
思路
模板题呀。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll n,m;
ll a[5000010];
void add(ll x,ll y){
for(ll i=x;i<=n;i+=i&(-i)){
a[i]+=y;
}
}
ll getsum(ll x){
ll sum=0;
for(ll i=x;i;i-=i&(-i)){
sum+=a[i];
}
return sum;
}
int main(){
scanf("%lld%lld",&n,&m);
for(ll i=1;i<=n;i++){
ll x;scanf("%lld",&x);
add(i,x);
}
for(ll i=1;i<=m;i++){
ll type;
scanf("%lld",&type);
if(type==1){
ll x,k;
scanf("%lld%lld",&x,&k);
add(x,k);
}
if(type==2){
ll x,y;
scanf("%lld%lld",&x,&y);
printf("%lld\n",getsum(y)-getsum(x-1));
}
}
}
#10114. 「一本通 4.1 例 2」数星星 Stars
题意
给定 $n$ 个点,定义每个点的等级是在该点左下方(含正左、正下)的点的数目,试统计每个等级有多少个点。
思路
这不就是裸的树状数组吗?
题目都按顺序(y的增序)。。。
#include<bits/stdc++.h>
using namespace std;
inline int read(){
char ch=getchar();int res=0,f=1;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9') res=res*10+ch-'0',ch=getchar();
return res*f;
}
inline void write(int x){
if(x<0) putchar('-'),x=-x;
if(x<10) putchar(x+'0');
else{
write(x/10);
putchar(x%10+'0');
}
}
int n,x,y,ans[1500010];
int a[1500010];
void add(int x,int y){
for(int i=x;i<=1500000;i+=i&(-i)){
a[i]+=y;
}
}
int getsum(int x){
int sum=0;
for(int i=x;i;i-=i&(-i)){
sum+=a[i];
}
return sum;
}
int main(){
n=read();
for(int i=1;i<=n;i++){
x=read();y=read();
int t=getsum(x+1);
ans[t]++;
add(x+1,1);
}
for(int i=0;i<n;i++){
write(ans[i]);putchar('\n');
}
return 0;
}
2019.1.28
#10116. 「一本通 4.1 练习 1」清点人数
题意
- 如果字母为
A,接下来是一个数 $m$,表示年级主任现在在第 $m$ 节车厢; - 如果字母为
B,接下来是两个数 $m,p$,表示在第 $m$ 节车厢有 $p$ 名学生上车; - 如果字母为
C,接下来是两个数 $m,p$,表示在第 $m$ 节车厢有 $p$ 名学生下车。
思路
当然是树状数组啦。。。
如果字母为 A ,那么$getsum(m)$
如果字母为 B ,那么$add(m,p)$
如果字母为 C ,那么$add(m,-p)$
好了呀。。。
#include<algorithm>
#include<bitset>
#include<complex>
#include<deque>
#include<exception>
#include<fstream>
#include<functional>
#include<iomanip>
#include<ios>
#include<iosfwd>
#include<iostream>
#include<istream>
#include<iterator>
#include<limits>
#include<list>
#include<locale>
#include<map>
#include<memory>
#include<new>
#include<numeric>
#include<ostream>
#include<queue>
#include<set>
#include<sstream>
#include<stack>
#include<stdexcept>
#include<streambuf>
#include<string>
#include<typeinfo>
#include<utility>
#include<valarray>
#include<vector>
#include<cctype>
#include<cerrno>
#include<cfloat>
#include<ciso646>
#include<climits>
#include<clocale>
#include<cmath>
#include<csetjmp>
#include<csignal>
#include<cstdarg>
#include<cstddef>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<ctime>
using namespace std;
inline int read(){
int res=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9') res=res*10+ch-'0',ch=getchar();
return res*f;
}
inline void write(int x){
if(x<0) putchar('-'),x=-x;
if(x<10) putchar(x+'0');
else{
write(x/10);
putchar(x%10+'0');
}
}
//queue<int> q;
//set<int> s;
//priority_queue<int> q1;
//priority_queue<int,vector<int>,greater<int> > q2;
//list<int> l;
//stack<int> s;
int n,k;
int c[500010];
void add(int x,int y){
for(int i=x;i<=n;i+=i&(-i)){
c[i]+=y;
}
}
int getsum(int x){
int sum=0;
for(int i=x;i;i-=i&(-i)){
sum+=c[i];
}
return sum;
}
int main(){
// freopen("code.in","r",stdin);freopen("code.out","w",stdout);
n=read();k=read();
for(int i=1;i<=k;i++){
char A;cin>>A;
int m,p;
if(A=='A'){
m=read();
write(getsum(m));putchar('\n');
}else if(A=='B'){
m=read();p=read();
add(m,p);
}else if(A=='C'){
m=read();p=read();
add(m,-p);
}
}
return 0;
}
#10117. 「一本通 4.1 练习 2」简单题
题意
有一个 $n$ 个元素的数组,每个元素初始均为 $0$。有 $m$ 条指令,要么让其中一段连续序列数字反转——$0$ 变 $1$,$1$ 变 $0$(操作 $1$),要么询问某个元素的值(操作 $2$)。
思路
当然是树状数组啦。。。
这里介绍C++的一大利器——位运算。
&在C++里叫做与运算。应该差不多吧。。大概就是这样的:(按一个个位运算)
1&1=1
0&1=0
1&0=0
0&0=0
|在C++里叫或运算
0|1=1
1|0=1
1|1=1
0|0=0
^在C++里叫异或(xor)
0^0=0
1^0=1
0^1=1
1^1=0
~在C++里叫取反
顾名思义。。。
~1=0
~0=1
然后你就会发现这道题可以用C++的异或+树状数组解决。
利用树状数组,做一个异或前缀和。然后在输出时异或一遍就好了。
(这道题的1操作就相当于异或1)
(然而我们知道x xor 1 xor 1还是等于x)
(所以对于每个1操作只需要先把l之前的xor 1,然后r+1之前的xor 1)
(对于每个2操作只需要把前面统统xor一遍)
你就完美的解决了这道题
#include<bits/stdc++.h>
using namespace std;//丑陋无比的头文件终于结束
inline int read(){
int res=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9') res=res*10+ch-'0',ch=getchar();
return res*f;
}//读入
inline void write(int x){
if(x<0) putchar('-'),x=-x;
if(x<10) putchar(x+'0');
else{
write(x/10);
putchar(x%10+'0');
}
}//输出
int n,k;
int c[500010];//不解释
void add(int x,int y){//修改
for(int i=x;i<=n;i+=i&(-i)){
c[i]^=y;//异或前缀和
}
}
int getsum(int x){//询问
int sum=0;
for(int i=x;i;i-=i&(-i)){
sum^=c[i];//询问异或
}
return sum;//返回啊
}
int main(){
n=read();k=read();//读入
for(int i=1;i<=k;i++){
char A;cin>>A;
int m,p;
if(A=='1'){//操作1
m=read();p=read();
add(m,1);//先将l之前的xor 1
add(p+1,1);//然后把r+1之前的xor 1
//那么l之前的数统统 xor 1 xor 1,抵消
}else if(A=='2'){
m=read();
write(getsum(m));putchar('\n');//询问输出
}
}
return 0;//结束了。。。
}
#133. 二维树状数组 1:单点修改,区间查询
题意
这是一道模板题。
给出一个 $n\times m$ 的零矩阵 $A$,你需要完成如下操作:
1 x y k:表示元素 $A_{x,y}$ 自增 $k$;2 a b c d:表示询问左上角为 $(a,b)$,右下角为 $(c,d)$ 的子矩阵内所有数的和。
思路
当然是树状数组啦。。。
模板题。不介绍。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll n,m;
ll a[5010][5010];
ll lowbit(ll x){
return (x&-x);
}
void add(ll x,ll y,ll k){
for(ll i=x;i<=n;i+=lowbit(i)){
for(ll j=y;j<=m;j+=lowbit(j)){
a[i][j]+=k;
}
}
}
ll getsum(ll x,ll y){
ll sum=0;
for(ll i=x;i>0;i-=lowbit(i)){
for(ll j=y;j>0;j-=lowbit(j)){
sum+=a[i][j];
}
}
return sum;
}
int main(){
scanf("%lld%lld",&n,&m);
ll type;
while(scanf("%lld",&type)!=EOF){
if(type==1){
ll x,y,k;
scanf("%lld%lld%lld",&x,&y,&k);
add(x,y,k);
}
if(type==2){
ll x1,y1,x2,y2;
scanf("%lld%lld%lld%lld",&x1,&y1,&x2,&y2);
printf("%lld\n",getsum(x2,y2)-getsum(x2,y1-1)-getsum(x1-1,y2)+getsum(x1-1,y1-1));
}
}
return 0;
}
#10119. 「一本通 4.2 例 1」数列区间最大值
题意
这是一道模板题。
输入一串数字,给你 $M$ 个询问,每次询问就给你两个数字 $X,Y$,要求你说出 $X$ 到 $Y$ 这段区间内的最大数。
思路
模板题。不介绍。
RMQ问题
#include<algorithm>
#include<bitset>
#include<complex>
#include<deque>
#include<exception>
#include<fstream>
#include<functional>
#include<iomanip>
#include<ios>
#include<iosfwd>
#include<iostream>
#include<istream>
#include<iterator>
#include<limits>
#include<list>
#include<locale>
#include<map>
#include<memory>
#include<new>
#include<numeric>
#include<ostream>
#include<queue>
#include<set>
#include<sstream>
#include<stack>
#include<stdexcept>
#include<streambuf>
#include<string>
#include<typeinfo>
#include<utility>
#include<valarray>
#include<vector>
#include<cstring>
#include<cmath>
using namespace std;
inline int read(){
char ch=getchar();int res=0,f=1;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9') res=res*10+ch-'0',ch=getchar();
return res*f;
}
inline void write(int zx){
if(zx<0) zx=-zx,putchar('-');
if(zx<10) putchar(zx+'0');
else{
write(zx/10);
putchar(zx%10+'0');
}
}
int n,m,a[100010],f[100010][20];
void ST(){
for(int i=1;i<=n;i++) f[i][0]=a[i];
for(int j=1;(1<<j)<=n;j++){
for(int i=1;i+(1<<j)-1<=n;i++){
f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
}
}
}
int RMQ(int l,int r){
int k=0;
while((1<<(k+1))<=r-l+1) k++;
return max(f[l][k],f[r-(1<<k)+1][k]);
}
int main(){
n=read();m=read();
for(int i=1;i<=n;i++) a[i]=read();
ST();
for(int i=1;i<=m;i++){
int l=read(),r=read();
write(RMQ(l,r));
putchar('\n');
}
return 0;
}
#10120. 「一本通 4.2 例 2」最敏捷的机器人
题意
首先,他们面前会有一排共 $n$ 个数,它们比赛看谁能最先把每连续 $k$ 个数中最大和最小值写下来,当然,这些机器人运算速度都很快,它们比赛的是谁写得快。
思路
模板题。不介绍。
RMQ问题分别做一个最大值与最小值。
#include<algorithm>
#include<bitset>
#include<complex>
#include<deque>
#include<exception>
#include<fstream>
#include<functional>
#include<iomanip>
#include<ios>
#include<iosfwd>
#include<iostream>
#include<istream>
#include<iterator>
#include<limits>
#include<list>
#include<locale>
#include<map>
#include<memory>
#include<new>
#include<numeric>
#include<ostream>
#include<queue>
#include<set>
#include<sstream>
#include<stack>
#include<stdexcept>
#include<streambuf>
#include<string>
#include<typeinfo>
#include<utility>
#include<valarray>
#include<vector>
#include<cstring>
#include<cmath>
#define ll long long
using namespace std;
inline ll read(){
char ch=getchar();ll res=0,f=1;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9') res=res*10+ch-'0',ch=getchar();
return res*f;
}
inline void write(ll zx){
if(zx<0) zx=-zx,putchar('-');
if(zx<10) putchar(zx+'0');
else{
write(zx/10);
putchar(zx%10+'0');
}
}
ll n,m,a[100010],f[100010][20],f2[100010][20];
void ST(){
for(ll i=1;i<=n;i++) f[i][0]=a[i];
for(ll j=1;(1<<j)<=n;j++) {
for(ll i=1;i+(1<<j)-1<=n;i++) {
f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
}
}
}
ll RMQ(ll l,ll r){
ll k=0;
while((1<<(k+1))<=r-l+1) k++;
return max(f[l][k],f[r-(1<<k)+1][k]);
}
void ST2(){
for(ll i=1;i<=n;i++) f2[i][0]=a[i];
for(ll j=1;(1<<j)<=n;j++) {
for(ll i=1;i+(1<<j)-1<=n;i++) {
f2[i][j]=min(f2[i][j-1],f2[i+(1<<(j-1))][j-1]);
}
}
}
ll RMQ2(ll l,ll r){
ll k=0;
while((1<<(k+1))<=r-l+1) k++;
return min(f2[l][k],f2[r-(1<<k)+1][k]);
}
int main(){
n=read();m=read();
for(ll i=1;i<=n;i++) a[i]=read();
ST();ST2();
for(ll i=1;i<=n-m+1;i++){
write(RMQ(i,i+m-1));
putchar(' ');
write(RMQ2(i,i+m-1));
putchar('\n');
}
return 0;
}
#10121. 「一本通 4.2 例 3」与众不同
题意
定义完美序列:一段连续的序列满足序列中的数互不相同。
想知道区间 $[L,R]$ 之间最长的完美序列长度。
思路
设$las[x]$表示盈利$x$最近出现位置。
设$st[i]$表示以第$i$个数结尾的最长完美序列的起始位置。 $$st[i]=max(st[i-1],las[a[i]+1])$$ 设$f[i]$表示以第$i$个数结尾的最长完美序列的长度 $$f[i]=i-st[i]+1$$ 由$st$的递推式可知,$st$的值是一个非递减的序列。
对于一个询问区间$[l_i,r_i]$,该区间内的$st$值可能会有两种情况:
- 左边一部分的$st$值不在区间内,即$<l_i$
- 右边一部分的$st$值不在区间内,即$\ge l_i$
由于$st$的值具有单调性,所以这个边界可以通过二分得到。设求出的边界为$mid$_i,可得: $$st[l_i...mid_i-1]<l_i$$
$$st[mid_i...r_i]\ge l_i$$
那么整个区间$[l_i,r_i]$的最长完美序列的长度可以分两部分来求。
-
左边:很显然为$mid_i-l_i$
-
右边:$MAX(m_i...r_i)$
所以右边的长度要使用ST表,即RMQ来求。
整个问题的时间复杂度: $$O((M+N) \times logN)$$
#include<algorithm>
#include<bitset>
#include<complex>
#include<deque>
#include<exception>
#include<fstream>
#include<functional>
#include<iomanip>
#include<ios>
#include<iosfwd>
#include<iostream>
#include<istream>
#include<iterator>
#include<limits>
#include<list>
#include<locale>
#include<map>
#include<memory>
#include<new>
#include<numeric>
#include<ostream>
#include<queue>
#include<set>
#include<sstream>
#include<stack>
#include<stdexcept>
#include<streambuf>
#include<string>
#include<typeinfo>
#include<utility>
#include<valarray>
#include<vector>
#include<cstring>
#include<cmath>
#define ll long long
const int N=2e5+5,M=1e6;
using namespace std;
inline ll read(){
char ch=getchar();ll res=0,f=1;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9') res=res*10+ch-'0',ch=getchar();
return res*f;
}
inline void write(ll zx){
if(zx<0) zx=-zx,putchar('-');
if(zx<10) putchar(zx+'0');
else{
write(zx/10);
putchar(zx%10+'0');
}
}
ll n,m,f[N][20],st[N],las[M<<1];
void ST(){
for(ll j=1;(1<<j)<=n;j++){
for(ll i=1;i+(1<<j)-1<=n;i++){
f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
}
}
}
ll RMQ(ll l,ll r){
ll k=0;
while((1<<(k+1))<=r-l+1) k++;
return max(f[l][k],f[r-(1<<k)+1][k]);
}
ll find(ll l,ll r){
if(st[l]==l) return l;
if(st[r]<l) return r+1;
int L=l,R=r;
while(L<=R){
int m=L+R>>1;
if(st[m]<l) L=m+1;
else R=m-1;
}
return L;
}
int main(){
n=read();m=read();
for(ll i=1;i<=n;i++){
int x=read();
st[i]=max(st[i-1],las[x+M]+1);
f[i][0]=i-st[i]+1;
las[x+M]=i;
}
ST();
for(ll i=1;i<=m;i++){
ll L,R;
L=read();R=read();L++;R++;
ll mid=find(L,R),ans=0,tmp;
if(mid>L) ans=mid-L;
if(mid<=R){
tmp=RMQ(mid,R);
ans=max(ans,tmp);
}
write(ans);putchar('\n');
}
return 0;
}
#10122. 「一本通 4.2 练习 1」天才的记忆
题意
给你一大串数字(编号为 $1$ 到 $N$,大小可不一定哦!),在你看过一遍之后,它便消失在你面前,随后问题就出现了,给你 $M$ 个询问,每次询问就给你两个数字 $A,B$,要求你瞬间就说出属于 $A$ 到 $B$ 这段区间内的最大数。
思路
典型的RMQ模板题啦。
先把一开始的一大串数字塞入RMQ。然后询问就好啦。没有一点坑。。。
#include<algorithm>
#include<bitset>
#include<complex>
#include<deque>
#include<exception>
#include<fstream>
#include<functional>
#include<iomanip>
#include<ios>
#include<iosfwd>
#include<iostream>
#include<istream>
#include<iterator>
#include<limits>
#include<list>
#include<locale>
#include<map>
#include<memory>
#include<new>
#include<numeric>
#include<ostream>
#include<queue>
#include<set>
#include<sstream>
#include<stack>
#include<stdexcept>
#include<streambuf>
#include<string>
#include<typeinfo>
#include<utility>
#include<valarray>
#include<vector>
#include<cstring>
#include<cmath>
#define ll long long
const int N=2e5+5,M=1e6;
using namespace std;
inline ll read(){
char ch=getchar();ll res=0,f=1;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9') res=res*10+ch-'0',ch=getchar();
return res*f;
}
inline void write(ll zx){
if(zx<0) zx=-zx,putchar('-');
if(zx<10) putchar(zx+'0');
else{
write(zx/10);
putchar(zx%10+'0');
}
}
ll n,m,f[N][20],st[N],las[M<<1];
void ST(){
for(ll j=1;(1<<j)<=n;j++){
for(ll i=1;i+(1<<j)-1<=n;i++){
f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
}
}
}
ll RMQ(ll l,ll r){
ll k=0;
while((1<<(k+1))<=r-l+1) k++;
return max(f[l][k],f[r-(1<<k)+1][k]);
}
ll find(ll l,ll r){
if(st[l]==l) return l;
if(st[r]<l) return r+1;
int L=l,R=r;
while(L<=R){
int m=L+R>>1;
if(st[m]<l) L=m+1;
else R=m-1;
}
return L;
}
int main(){
n=read();
for(ll i=1;i<=n;i++){
int x=read();
f[i][0]=x;
}
ST();m=read();
for(ll i=1;i<=m;i++){
ll L,R;
L=read();R=read();int ans=RMQ(L,R);
write(ans);putchar('\n');
}
return 0;
}
#10123. 「一本通 4.2 练习 2」Balanced Lineup
题意
FJ 准备了 $Q$ 个可能的牛的选择和所有牛的身高。他想知道每一组里面最高和最低的牛的身高差别。
思路
典型的RMQ模板题啦。
先把一开始的一大串数字塞入RMQ。然后询问就好啦。没有一点坑。。。
注意RMQ2次就好了啊
#include<algorithm>
#include<bitset>
#include<complex>
#include<deque>
#include<exception>
#include<fstream>
#include<functional>
#include<iomanip>
#include<ios>
#include<iosfwd>
#include<iostream>
#include<istream>
#include<iterator>
#include<limits>
#include<list>
#include<locale>
#include<map>
#include<memory>
#include<new>
#include<numeric>
#include<ostream>
#include<queue>
#include<set>
#include<sstream>
#include<stack>
#include<stdexcept>
#include<streambuf>
#include<string>
#include<typeinfo>
#include<utility>
#include<valarray>
#include<vector>
#include<cstring>
#include<cmath>
#define ll long long
const int N=2e5+5,M=1e6;
using namespace std;
inline ll read(){
char ch=getchar();ll res=0,f=1;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9') res=res*10+ch-'0',ch=getchar();
return res*f;
}
inline void write(ll zx){
if(zx<0) zx=-zx,putchar('-');
if(zx<10) putchar(zx+'0');
else{
write(zx/10);
putchar(zx%10+'0');
}
}
ll n,m,f[N][20],st[N],las[M<<1],f2[N][20];
void ST(){
for(ll j=1;(1<<j)<=n;j++){
for(ll i=1;i+(1<<j)-1<=n;i++){
f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
}
}
}
ll RMQ(ll l,ll r){
ll k=0;
while((1<<(k+1))<=r-l+1) k++;
return max(f[l][k],f[r-(1<<k)+1][k]);
}
void ST2(){
for(ll j=1;(1<<j)<=n;j++){
for(ll i=1;i+(1<<j)-1<=n;i++){
f2[i][j]=min(f2[i][j-1],f2[i+(1<<(j-1))][j-1]);
}
}
}
ll RMQ2(ll l,ll r){
ll k=0;
while((1<<(k+1))<=r-l+1) k++;
return min(f2[l][k],f2[r-(1<<k)+1][k]);
}
int main(){
n=read();m=read();
for(ll i=1;i<=n;i++){
int x=read();
f2[i][0]=f[i][0]=x;
}
ST();ST2();
for(ll i=1;i<=m;i++){
ll L,R;
L=read();R=read();int ans=RMQ(L,R)-RMQ2(L,R);
write(ans);putchar('\n');
}
return 0;
}
#2597. 「NOIP2011」选择客栈
题意
有$n$个客栈,每个客栈都配有咖啡馆。有两名旅客想住在同色调的客栈中,又想在两客栈之间的咖啡馆中小聚,咖啡馆的价钱不能高于$p$。
对于 $100%$ 的数据,有 $2\leq n\leq2\times 10^6$,$0<k\leq10^4$ ,$0\leq p\leq100$,$0\leq$ 最低消费 $\leq100$ 。
思路
$n$的范围那么大,$k$的范围那么小。那么暴力吧。
设$h_i$表示目前颜色$i$的客栈数量,$las_i$表示最近的颜色为$i$的客栈的编号。
然后$O(n)$扫一遍就好了啊。
#include<algorithm>
#include<bitset>
#include<complex>
#include<deque>
#include<exception>
#include<fstream>
#include<functional>
#include<iomanip>
#include<ios>
#include<iosfwd>
#include<iostream>
#include<istream>
#include<iterator>
#include<limits>
#include<list>
#include<locale>
#include<map>
#include<memory>
#include<new>
#include<numeric>
#include<ostream>
#include<queue>
#include<set>
#include<sstream>
#include<stack>
#include<stdexcept>
#include<streambuf>
#include<string>
#include<typeinfo>
#include<utility>
#include<valarray>
#include<vector>
#include<cstring>
#include<cmath>
#define ll long long
const int N=2e5+5,M=1e6;
using namespace std;
inline ll read(){
char ch=getchar();ll res=0,f=1;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9') res=res*10+ch-'0',ch=getchar();
return res*f;
}
inline void write(ll zx){
if(zx<0) zx=-zx,putchar('-');
if(zx<10) putchar(zx+'0');
else{
write(zx/10);
putchar(zx%10+'0');
}
}
ll n,m,color,price,now,las[N],h[N],sum[N],ans,p;
int main(){
n=read();m=read();p=read();
for(ll i=1;i<=n;i++){
color=read(),price=read();//读入
if(price<=p) now=i;//价钱要小于或等于p
if(now>=las[color]) sum[color]=h[color];//如果比上一个颜色相同的近,直接加上方案数
ans+=sum[color];//更新ANS
h[color]++;las[color]=i;//更新LAS和H
}
write(ans);putchar('\n');//输出
return 0;
}
#130. 树状数组 1 :单点修改,区间查询
题意
这是一道模板题。
给定Q个操作:
1 i x:给定 $i,x$,将 $a[i]$ 加上 $x$;2 l r:给定 $l,r$,求 $\sum_{i=l}^ra[i]$ 的值(换言之,求 $a[l]+a[l+1]+\dots+a[r]$ 的值)。
思路
模板题呀。但线段树可以过啊。
粘模板了。。。
#include<bits/stdc++.h>
#define N 10000000+10
#define ll long long
using namespace std;
ll n,m,a[N],add[N*4+10];
ll tree[N*4+10];
void pushup(ll id){
tree[id]=tree[id<<1]+tree[(id<<1)|1];
}
void build(ll id,ll l,ll r){
if(l==r) tree[id]=a[l];
else{
ll mid=l+((r-l)>>1);
build(id<<1,l,mid);
build((id<<1)|1,mid+1,r);
pushup(id);
}
}
void pushdown(ll id,ll l,ll r){
if(add[id]!=0){
add[id<<1]+=add[id];
add[(id<<1)|1]+=add[id];
ll mid=l+((r-l)>>1);
tree[id<<1]+=add[id]*(mid-l+1);
tree[(id<<1)|1]+=add[id]*(r-mid);
add[id]=0;
}
}
void update(ll id,ll l,ll r,ll ql,ll qr,ll val){
if(ql<=l&&qr>=r){
add[id]+=val;
tree[id]+=val*(r-l+1);
return ;
}
pushdown(id,l,r);
ll mid=l+((r-l)>>1);
if(ql<=mid) update(id<<1,l,mid,ql,qr,val);
if(qr>=mid+1) update((id<<1)|1,mid+1,r,ql,qr,val);
pushup(id);
}
ll query(ll id,ll l,ll r,ll ql,ll qr){
if(ql<=l&&qr>=r) return tree[id];
pushdown(id,l,r);
ll mid=l+((r-l)>>1);
ll ans=0;
if(ql<=mid) ans+=query(id<<1,l,mid,ql,qr);
if(qr>=mid+1) ans+=query((id<<1)|1,mid+1,r,ql,qr);
return ans;
}
int main(){
scanf("%lld%lld",&n,&m);
for(ll i=1;i<=n;i++) scanf("%lld",&a[i]);
build(1,1,n);
for(ll i=1;i<=m;i++){
ll type;
scanf("%lld",&type);
if(type==1){
ll x,y,k;
scanf("%lld%lld",&y,&k);
update(1,1,n,y,y,k);
}
if(type==2){
ll x,y;
scanf("%lld%lld",&x,&y);
ll temp=query(1,1,n,x,y);
printf("%lld\n",temp);
}
}
return 0;
}
#132. 树状数组 3 :区间修改,区间查询
题意
这是一道模板题。\r\n\r\n给定数列 $a[1], a[2], \dots, a[n]$,你需要依次进行 $q$ 个操作,操作有两类:
1 l r x:给定 $l,r,x$,对于所有 $i\in[l,r]$,将 $a[i]$ 加上 $x$(换言之,将 $a[l], a[l+1], \dots, a[r]$ 分别加上 $x$);2 l r:给定 $l,r$,求 $\sum_{i=l}^ra[i]$ 的值(换言之,求 $a[l]+a[l+1]+\dots+a[r]$ 的值)。
思路
模板题呀。但线段树可以过啊。
粘模板了。。。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll n,m,a[1000010],add[1000000*4+10];
ll tree[1000000*4+10];
void pushup(ll id){
tree[id]=tree[id<<1]+tree[(id<<1)|1];
}
void build(ll id,ll l,ll r){
if(l==r) tree[id]=a[l];
else{
ll mid=l+((r-l)>>1);
build(id<<1,l,mid);
build((id<<1)|1,mid+1,r);
pushup(id);
}
}
void pushdown(ll id,ll l,ll r){
if(add[id]!=0){
add[id<<1]+=add[id];
add[(id<<1)|1]+=add[id];
ll mid=l+((r-l)>>1);
tree[id<<1]+=add[id]*(mid-l+1);
tree[(id<<1)|1]+=add[id]*(r-mid);
add[id]=0;
}
}
void update(ll id,ll l,ll r,ll ql,ll qr,ll val){
if(ql<=l&&qr>=r){
add[id]+=val;
tree[id]+=val*(r-l+1);
return ;
}
pushdown(id,l,r);
ll mid=l+((r-l)>>1);
if(ql<=mid) update(id<<1,l,mid,ql,qr,val);
if(qr>=mid+1) update((id<<1)|1,mid+1,r,ql,qr,val);
pushup(id);
}
ll query(ll id,ll l,ll r,ll ql,ll qr){
if(ql<=l&&qr>=r) return tree[id];
pushdown(id,l,r);
ll mid=l+((r-l)>>1);
ll ans=0;
if(ql<=mid) ans+=query(id<<1,l,mid,ql,qr);
if(qr>=mid+1) ans+=query((id<<1)|1,mid+1,r,ql,qr);
return ans;
}
int main(){
scanf("%lld%lld",&n,&m);
for(ll i=1;i<=n;i++) scanf("%lld",&a[i]);
build(1,1,n);
for(ll i=1;i<=m;i++){
ll type;
scanf("%lld",&type);
if(type==1){
ll x,y,k;
scanf("%lld%lld%lld",&x,&y,&k);
update(1,1,n,x,y,k);
}
if(type==2){
ll x,y;
scanf("%lld%lld",&x,&y);
ll temp=query(1,1,n,x,y);
printf("%lld\n",temp);
}
}
return 0;
}
#10127. 「一本通 4.3 练习 1」最大数
题意
给定一个正整数数列 $a_1, a_2, a_3, \cdots , a_n$,每一个数都在 $0\sim p – 1$ 之间。可以对这列数进行两种操作:
-
添加操作:向序列后添加一个数,序列长度变成 $n + 1$;
-
询问操作:询问这个序列中最后 $L$ 个数中最大的数是多少。
程序运行的最开始,整数序列为空。写一个程序,读入操作的序列,并输出询问操作的答案。
思路
模板题呀。
#include<bits/stdc++.h>
#define ll long long
#define MAXNUM 200000*4+10
using namespace std;
struct node{
ll l,r,lef,rig,c;
}tree[MAXNUM];
ll n,m,q,len,las;
void build(ll l,ll r){
ll root=++len;
tree[root].l=l;tree[root].r=r;tree[root].lef=tree[root].rig=-1;
if(l<r){
ll mid=(l+r)/2;
tree[root].lef=len+1;build(l,mid);
tree[root].rig=len+1;build(mid+1,r);
}
}
void update(ll root,ll x,ll k){
if(tree[root].l==tree[root].r){tree[root].c=k;return ;}
ll lef=tree[root].lef,rig=tree[root].rig;
ll mid=(tree[root].l+tree[root].r)/2;
if(x<=mid) update(lef,x,k);
else update(rig,x,k);
tree[root].c=max(tree[lef].c,tree[rig].c);
}
ll query(ll root,ll l,ll r){
if(tree[root].l>=l&&tree[root].r<=r) return tree[root].c;
ll lef=tree[root].lef,rig=tree[root].rig;
ll mid=(tree[root].l+tree[root].r)/2;
if(r<=mid) return query(lef,l,r);
else if(mid<l) return query(rig,l,r);
else return max(query(lef,l,mid),query(rig,mid+1,r));
}
int main(){
scanf("%lld%lld",&m,&q);
build(1,m);
while(m--){
char s;cin>>s;
if(s=='A'){
ll x;scanf("%lld",&x);n++;
update(1,n,(x+las)%q);
}else{
ll x;scanf("%lld",&x);
las=query(1,n-x+1,n);
printf("%lld\n",las);
}
}
}
#10128. 「一本通 4.3 练习 2」花神游历各国
题意
每一次旅行中,花神会选择一条旅游路线,它在那一串国家中是连续的一段,这次旅行带来的开心值是这些国家的喜欢度的总和,当然花神对这些国家的喜欢程序并不是恒定的,有时会突然对某些国家产生反感,使他对这些国家的喜欢度 $\delta$ 变为 $\sqrt \delta$(可能是花神虐爆了那些国家的 OI,从而感到乏味)。
现在给出花神每次的旅行路线,以及开心度的变化,请求出花神每次旅行的开心值。
思路
为了使时间复杂度降低,我们可以发现:$\sqrt 1=1$所以,最大数字$10^9$操作较少次数便能到$1$。所以在操作前判断一下,如果区间内都是$1$即可跳过。
#include<bits/stdc++.h>
#define ll long long
#define MAXNUM 1000000*4+10
using namespace std;
struct node{
ll l,r,lef,rig;
ll val,Max;
}tree[210000];
ll a[110000],len,n,m;
void build(ll l,ll r){
ll root=++len;
tree[root].l=l;tree[root].r=r;tree[root].lef=tree[root].rig=-1;
if(l==r)tree[root].val=tree[root].Max=a[l];
else{
ll mid=(l+r)/2;
ll lef=tree[root].lef=len+1;build(l,mid);
ll rig=tree[root].rig=len+1;build(mid+1,r);
tree[root].val=tree[lef].val+tree[rig].val;
tree[root].Max=max(tree[lef].Max,tree[rig].Max);
}
}
void update(ll root,ll l,ll r){
if(tree[root].Max<2) return ;
if(tree[root].l==tree[root].r){tree[root].val=sqrt(tree[root].val);tree[root].Max=tree[root].val;return ;}
ll lef=tree[root].lef,rig=tree[root].rig,mid=(tree[root].l+tree[root].r)/2;
if(r<=mid) update(lef,l,r);
else if(mid<l) update(rig,l,r);
else update(lef,l,mid),update(rig,mid+1,r);
tree[root].val=tree[lef].val+tree[rig].val;
tree[root].Max=max(tree[lef].Max,tree[rig].Max);
}
ll query(ll root,ll l,ll r){
if(tree[root].l>=l&&tree[root].r<=r) return tree[root].val;
ll lef=tree[root].lef,rig=tree[root].rig,mid=(tree[root].l+tree[root].r)/2;
if(r<=mid) return query(lef,l,r);
else if(mid<l) return query(rig,l,r);
else return query(lef,l,mid)+query(rig,mid+1,r);
}
int main(){
scanf("%lld",&n);
for(ll i=1;i<=n;i++) scanf("%lld",&a[i]);
build(1,n);
scanf("%lld",&m);
while(m--){
char s;cin>>s;
if(s=='2'){
ll x,y;scanf("%lld%lld",&x,&y);
update(1,x,y);
}else{
ll x,y;scanf("%lld%lld",&x,&y);
printf("%lld\n",query(1,x,y));
}
}
return 0;
}
#10129. 「一本通 4.3 练习 3」维护序列
题意
有长为 $n$ 的数列,不妨设为 $a_1,a_2,\cdots ,a_n$。有如下三种操作形式:
- 把数列中的一段数全部乘一个值;
- 把数列中的一段数全部加一个值;
- 询问数列中的一段数的和,由于答案可能很大,你只需输出这个数模 $P$ 的值。
思路
线段树瞎搞。乘法的优先级要高一些。
注意MOD
#include<bits/stdc++.h>
#define N 10000000+10
#define ll long long
using namespace std;
ll n,m,a[N],add[N*4+10],mod,p,mul[N*4+10];
ll tree[N*4+10];
void pushup(ll id){
tree[id]=tree[id<<1]+tree[(id<<1)|1];
tree[id]%=mod;
}
void push_down(ll cur,ll l,ll r,ll mid){
if(mul[cur]==1&&add[cur]==0) return;
mul[cur<<1]=mul[cur<<1]*mul[cur]%mod;
add[cur<<1]=(add[cur<<1]*mul[cur]%mod+add[cur])%mod;
tree[cur<<1]=(tree[cur<<1]*mul[cur]%mod+add[cur]*(ll)(mid-l+1)%mod)%mod;
mul[cur<<1|1]=mul[cur<<1|1]*mul[cur]%mod;
add[cur<<1|1]=(add[cur<<1|1]*mul[cur]%mod+add[cur])%mod;
tree[cur<<1|1]=(tree[cur<<1|1]*mul[cur]%mod+add[cur]*(ll)(r-mid)%mod)%mod;
mul[cur]=1;
add[cur]=0;
return;
}
void update(ll id,ll l,ll r,ll ql,ll qr,ll val){
if(ql<=l&&qr>=r){
add[id]+=val;add[id]%=mod;
tree[id]=(tree[id]+(ll)(r-l+1)*val%mod)%mod;
return ;
}
push_down(id,l,r,l+r>>1);
ll mid=l+((r-l)>>1);
if(ql<=mid) update(id<<1,l,mid,ql,qr,val);
if(qr>=mid+1) update((id<<1)|1,mid+1,r,ql,qr,val);
pushup(id);
}
void updatemul(ll cur,ll L,ll R,ll l,ll r,ll x){
if(L>=l&&R<=r){
mul[cur]=mul[cur]*(ll)x%mod;
add[cur]=add[cur]*(ll)x%mod;
tree[cur]=tree[cur]*(ll)x%mod;
return;
}
ll mid=L+R>>1;
push_down(cur,L,R,mid);
if(l<=mid) updatemul(cur<<1,L,mid,l,r,x);
if(r>mid) updatemul(cur<<1|1,mid+1,R,l,r,x);
pushup(cur);
}
ll query(ll id,ll L,ll R,ll l,ll r){
if(L>=l&&R<=r) return tree[id]%mod;
ll mid=L+R>>1;
ll ans=0;
push_down(id,L,R,mid);
if(l<=mid) ans=(ans+query(id<<1,L,mid,l,r))%mod;
if(r>mid) ans=(ans+query(id<<1|1,mid+1,R,l,r))%mod;
pushup(id);
return ans;
}
void build(ll L,ll R,ll x,ll y,ll cur){
mul[cur]=1;add[cur]=0;tree[cur]+=y;
if(L==R) return;
ll mid=L+R>>1;
if(x>mid) build(mid+1,R,x,y,cur<<1|1);
else build(L,mid,x,y,cur<<1);
pushup(cur);
}
int main(){
scanf("%lld%lld",&n,&mod);
for(ll i=1;i<=n;i++) scanf("%lld",&a[i]),build(1,n,i,a[i]%mod,1);
scanf("%lld",&m);
for(ll i=1;i<=m;i++){
ll type;
scanf("%lld",&type);
if(type==1){
ll x,y,k;
scanf("%lld%lld%lld",&x,&y,&k);
updatemul(1,1,n,x,y,k);
}
if(type==2){
ll x,y,k;
scanf("%lld%lld%lld",&x,&y,&k);
update(1,1,n,x,y,k);
}
if(type==3){
ll x,y;
scanf("%lld%lld",&x,&y);
ll temp=query(1,1,n,x,y);
printf("%lld\n",temp%mod);
}
}
return 0;
}
2018.1.29
#10202. 「一本通 6.2 练习 5」樱花
题意
求不定方程: $$ \frac{1}{x}+\frac{1}{y}=\frac{1}{n!} $$ 的正整数解 $(x,y)$ 的数目。
思路
$$ \frac{1}{x}+\frac{1}{y}=\frac{1}{n!} $$
$$ \frac{y}{xy}+\frac{x}{xy}=\frac{1}{n!} $$
$$ \frac{x+y}{xy}=\frac{1}{n!} $$
$$ n!\times(x+y)=xy $$
$$ x+y=\frac{xy}{n!} $$
$$ (x-n!)*(y-n!)=(n!)^2 $$
#include<bits/stdc++.h>
using namespace std;
long long f[1000010],v[1000010],tot,ans[1000010],Ans=0;
long long n;
void prime(){
for(long long i=2;i<=1000000;i++){
if(!v[i]) v[i]=i,f[++tot]=i;
for(long long j=1;j<=tot;j++){
if(f[j]>v[i]||f[j]>1000000/i) break;
v[i*f[j]]=f[j];
}
}
}
int main(){
scanf("%lld",&n);
prime();long long tmp=n;
memset(ans,0,sizeof(ans));Ans=1;
for(int i=1;f[i]<=n&&i<=tot;i++){
long long tmp=0;
for(long long j=f[i];j<=n;j*=f[i]){
tmp+=n/j;
tmp%=1000000007;
}
Ans*=2*tmp+1;
Ans%=1000000007;
}
printf("%lld\n",Ans);
}
#10147. 「一本通 5.1 例 1」石子合并
题意
将 $n$ 堆石子绕圆形操场排放,现要将石子有序地合并成一堆。规定每次只能选相邻的两堆合并成新的一堆,并将新的一堆的石子数记做该次合并的得分。
请编写一个程序,读入堆数 $n$ 及每堆的石子数,并进行如下计算:
- 选择一种合并石子的方案,使得做 $n-1$ 次合并得分总和最大。
- 选择一种合并石子的方案,使得做 $n-1$ 次合并得分总和最小。
思路
DP水过去。。。
求最大值
设$f[i][j]$表示区间$[i,j]$得分的最大值。
很容易可以想到: $$f[i][j]=max(f[i][k]+f[k+1][j]+dist(i,j)))$$
$$dist(i,j)=a[i]+a[i+1]+...+a[j-1]+a[j]$$
所以我们设$sum[i]=a[1]+a[2]+...+a[i-1]+a[i]$
可得: $$sum[i]=sum[i-1]+a[i]$$ 那么: $$f[i][j]=max(f[i][j],f[i][k]+f[k+1][j]+sum[j]-sum[i-1])$$ 但是,仔细读题,发现是环。。。!
所以我们将环转换成链,即将$a$数组往后$n$个单位复制一遍。
最小值
与最大值差不多。改一个符号$max------>min$。
#include<algorithm>
#include<bitset>
#include<complex>
#include<deque>
#include<exception>
#include<fstream>
#include<functional>
#include<iomanip>
#include<ios>
#include<iosfwd>
#include<iostream>
#include<istream>
#include<iterator>
#include<limits>
#include<list>
#include<locale>
#include<map>
#include<memory>
#include<new>
#include<numeric>
#include<ostream>
#include<queue>
#include<set>
#include<sstream>
#include<stack>
#include<stdexcept>
#include<streambuf>
#include<string>
#include<typeinfo>
#include<utility>
#include<valarray>
#include<vector>
#include<cctype>
#include<cerrno>
#include<cfloat>
#include<ciso646>
#include<climits>
#include<clocale>
#include<cmath>
#include<csetjmp>
#include<csignal>
#include<cstdarg>
#include<cstddef>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<ctime>
#define E 200010
using namespace std;
inline int read(){
int res=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9') res=res*10+ch-'0',ch=getchar();
return res*f;
}
inline void write(int x){
if(x<0) putchar('-'),x=-x;
if(x<10) putchar(x+'0');
else{
write(x/10);
putchar(x%10+'0');
}
}
int n,f[210][210],a[210],sum[210],ans;
int main(){
n=read();
for(int i=1;i<=n;i++) a[i]=read(),a[i+n]=a[i];
for(int i=1;i<=n*2;i++) sum[i]=sum[i-1]+a[i];
memset(f,63,sizeof(f));
for(int i=1;i<=n*2;i++) f[i][i]=0;
for(int L=2;L<=n;L++){
for(int i=1;i<=n*2-L+1;i++){
int j=i+L-1;
for(int k=i;k<j;k++){
f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]+sum[j]-sum[i-1]);
}
}
}
ans=2e9;
for(int i=1;i<=n;i++){
ans=min(ans,f[i][i+n-1]);
}
write(ans);putchar('\n');
memset(f,0,sizeof(f));
for(int i=1;i<=n*2;i++) f[i][i]=0;
for(int L=2;L<=n;L++){
for(int i=1;i<=n*2-L+1;i++){
int j=i+L-1;
for(int k=i;k<j;k++){
f[i][j]=max(f[i][j],f[i][k]+f[k+1][j]+sum[j]-sum[i-1]);
}
}
}
ans=0;
for(int i=1;i<=n;i++){
ans=max(ans,f[i][i+n-1]);
}
write(ans);putchar('\n');
return 0;
}
#10148. 「一本通 5.1 例 2」能量项链
题意
有$n$颗珠子,每个珠子都有自己的标记,现将珠子串成项链(环),每相邻的两颗珠子可以通过聚合释放出能量=三颗珠子的标记之积,并合并成一颗更大的珠子,问聚合成一颗珠子后最大释放的能量。
比如有一串项链:$2-->3-->5-->10$,那么把第一颗与第四颗珠子合并后产生的能量$=2\times3\times10$。那么这一串项链最多可释放:$(((4\bigotimes1)\bigotimes2)\bigotimes3)=(10\times2\times3)+10\times3\times5+10\times10\times5=710$
思路
设$f[i][j]$表示区间$[i,j]$的珠子合并后产生能量的最大值。 $$f[i][j]=max(f[i][k]+f[k+1][j]+a[i]*a[j+1]*a[k+1])$$ 也是把环展开就好了。。。233333333333.............
#include<algorithm>
#include<bitset>
#include<complex>
#include<deque>
#include<exception>
#include<fstream>
#include<functional>
#include<iomanip>
#include<ios>
#include<iosfwd>
#include<iostream>
#include<istream>
#include<iterator>
#include<limits>
#include<list>
#include<locale>
#include<map>
#include<memory>
#include<new>
#include<numeric>
#include<ostream>
#include<queue>
#include<set>
#include<sstream>
#include<stack>
#include<stdexcept>
#include<streambuf>
#include<string>
#include<typeinfo>
#include<utility>
#include<valarray>
#include<vector>
#include<cctype>
#include<cerrno>
#include<cfloat>
#include<ciso646>
#include<climits>
#include<clocale>
#include<cmath>
#include<csetjmp>
#include<csignal>
#include<cstdarg>
#include<cstddef>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<ctime>
#define E 200010
using namespace std;
inline int read(){
int res=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9') res=res*10+ch-'0',ch=getchar();
return res*f;
}
inline void write(int x){
if(x<0) putchar('-'),x=-x;
if(x<10) putchar(x+'0');
else{
write(x/10);
putchar(x%10+'0');
}
}
//queue<int> q;
//set<int> s;
//priority_queue<int> q1;
//priority_queue<int,vector<int>,greater<int> > q2;
//list<int> l;
//stack<int> s;
int n,f[210][210],a[210],sum[210],ans;
int main(){
n=read();
for(int i=1;i<=n;i++) a[i]=read(),a[i+n]=a[i];
memset(f,0,sizeof(f));
for(int i=1;i<=n*2;i++) f[i][i]=0;
for(int L=2;L<=n;L++){
for(int i=1;i<=n*2-L+1;i++){
int j=i+L-1;
for(int k=i;k<=j-1;k++){
f[i][j]=max(f[i][j],f[i][k]+f[k+1][j]+a[i]*a[j+1]*a[k+1]);
}
}
}
ans=0;
for(int i=1;i<=n;i++){
ans=max(ans,f[i][i+n-1]);
}
write(ans);putchar('\n');
return 0;
}
2019.1.30
#10149. 「一本通 5.1 例 3」凸多边形的划分
题意
给定一个具有 $N$ 个顶点的凸多边形,将顶点从 $1$ 至 $N$ 标号,每个顶点的权值都是一个正整数。将这个凸多边形划分成 $N-2$ 个互不相交的三角形,试求这些三角形顶点的权值乘积和至少为多少。
思路
首先随便搞一个多边形:

然后给它顺时针每个顶点表上序号:
然后枚举$i,j$,要求:$i+1<j$,然后给$i,j$连一条线,分割出来另一个多边形:多边形23456
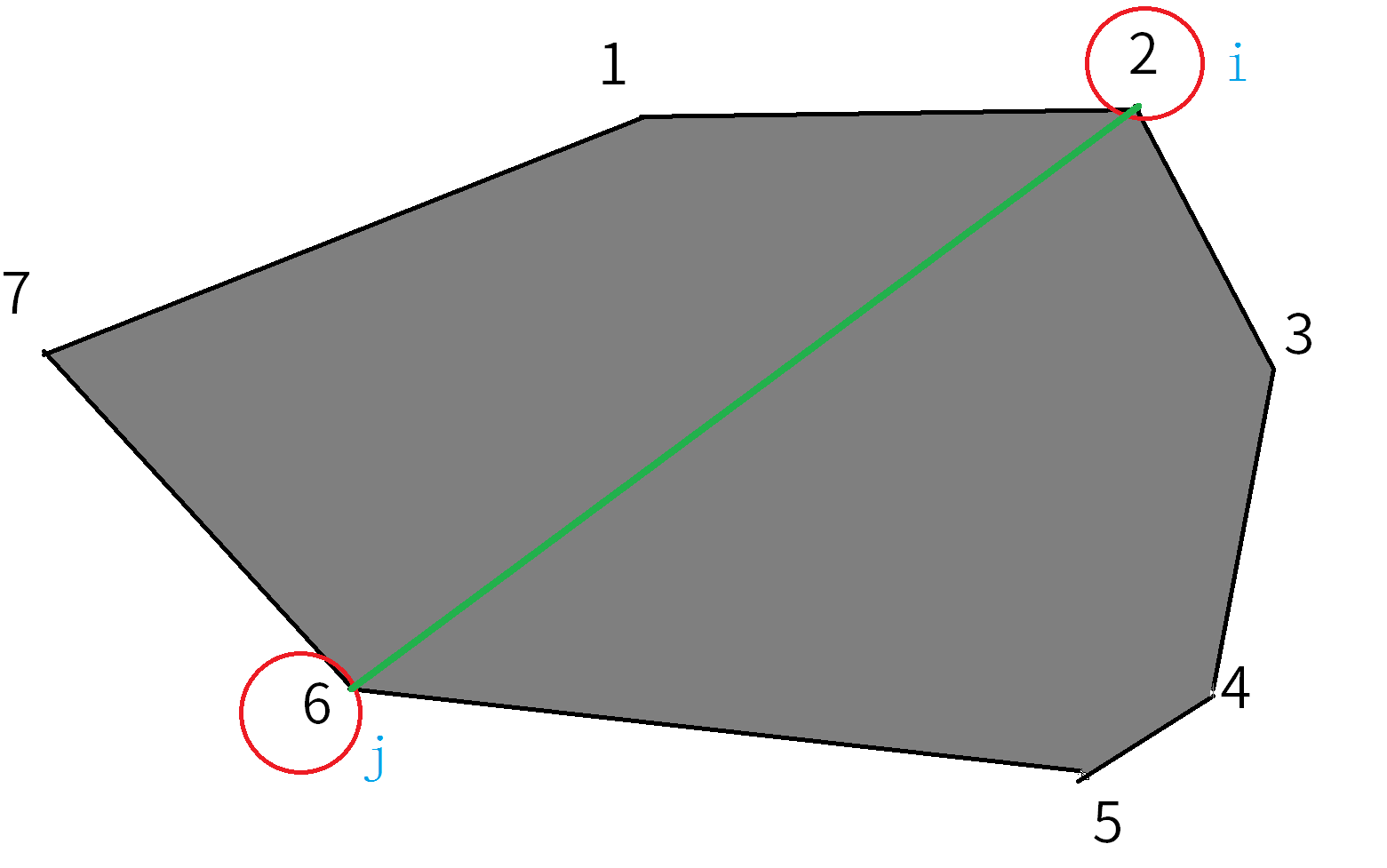
然后在$i,j$范围内枚举$k$,使得多边形23456又可以分割。
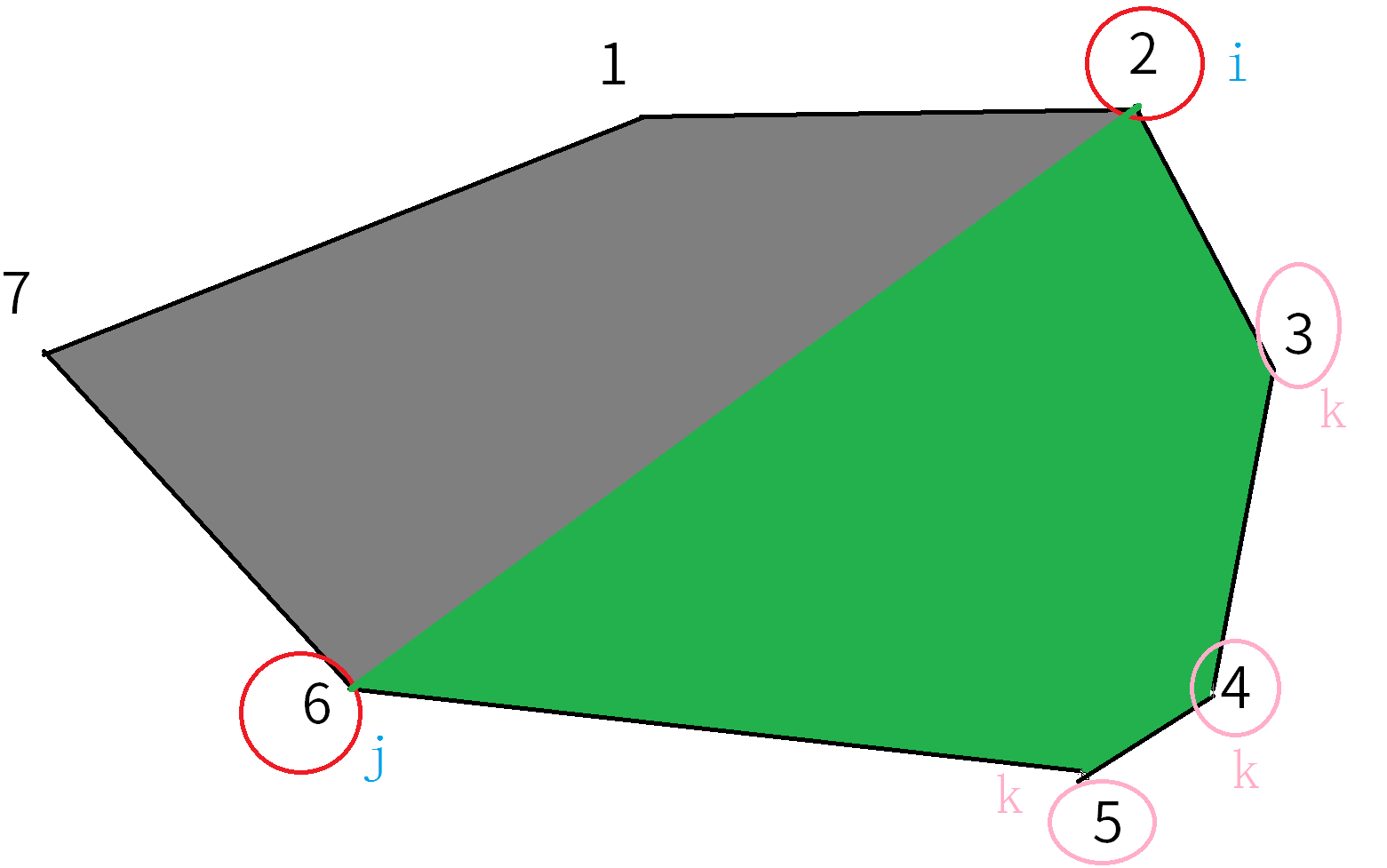
分割成如下图:
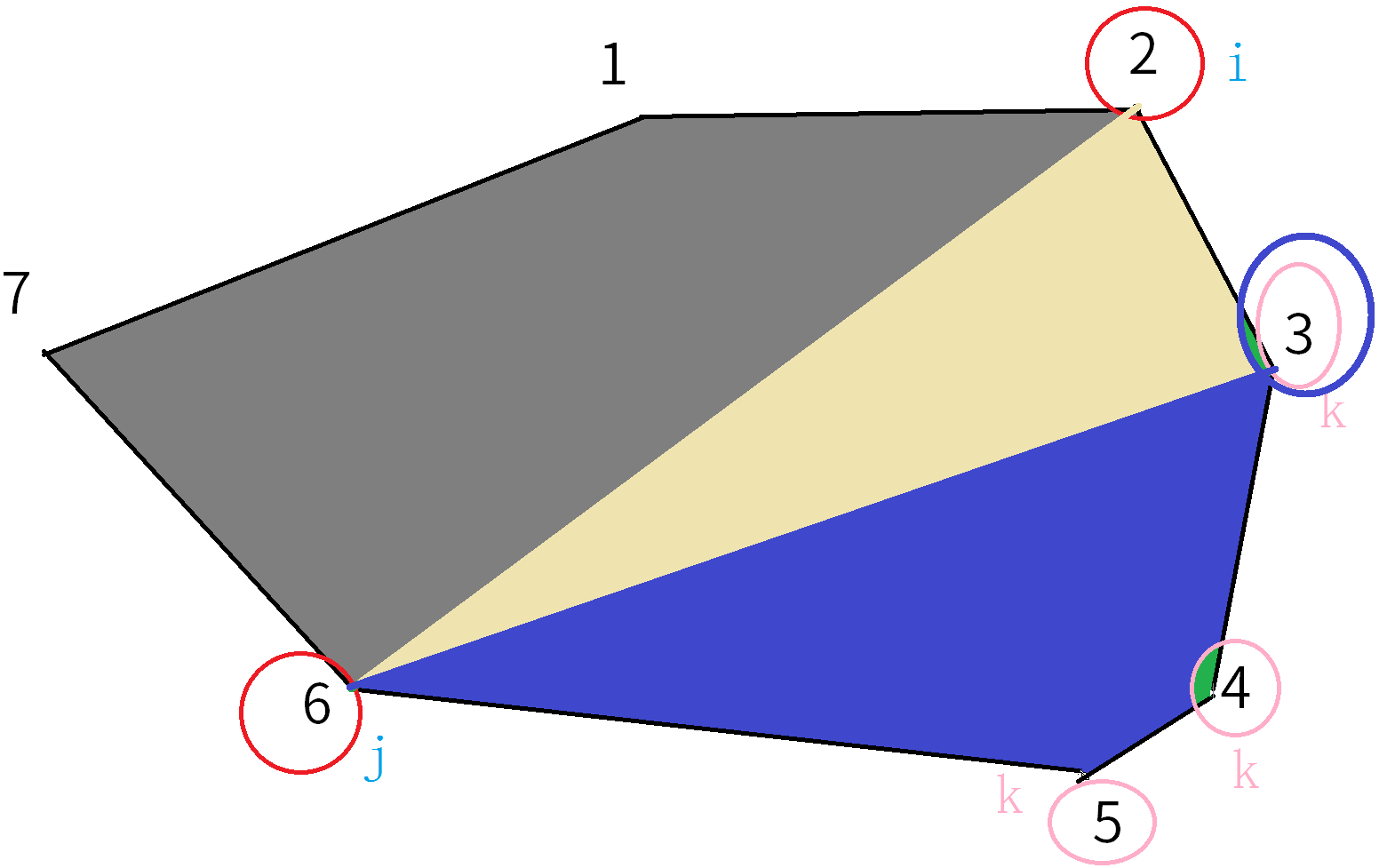
设$f[i][j]$表示把$i,j$的多边形切割成三角形后的权值乘积之和的最小值。
可得: $$f[i][j]=min{f[i][k]+f[k][j]+a[i]*a[j]*a[k]}(0<i<j<k\leq n)$$ 初始化: $$f[i][j]=inf(0<i\leq n,0<j\leq n)$$
$$f[i][i+1]=0(0<i<n)$$
时间复杂度:$O(n^3)$
输出结果:$f[1][n]$
当然,这道题范围特别大:对于 $100\%$ 的数据,有 $N\le 50$,每个点权值小于 $10^9$。三个数相乘最高可达$10^{27}$,所以需要使用高精度。这里使用了C++大数类,转自代号4101
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1000;
struct bign{
int d[maxn], len;
void clean() { while(len > 1 && !d[len-1]) len--; }
bign() { memset(d, 0, sizeof(d)); len = 1; }
bign(int num) { *this = num; }
bign(char* num) { *this = num; }
bign operator = (const char* num){
memset(d, 0, sizeof(d)); len = strlen(num);
for(int i = 0; i < len; i++) d[i] = num[len-1-i] - '0';
clean();
return *this;
}
bign operator = (int num){
char s[20]; sprintf(s, "%d", num);
*this = s;
return *this;
}
bign operator + (const bign& b){
bign c = *this; int i;
for (i = 0; i < b.len; i++){
c.d[i] += b.d[i];
if (c.d[i] > 9) c.d[i]%=10, c.d[i+1]++;
}
while (c.d[i] > 9) c.d[i++]%=10, c.d[i]++;
c.len = max(len, b.len);
if (c.d[i] && c.len <= i) c.len = i+1;
return c;
}
bign operator - (const bign& b){
bign c = *this; int i;
for (i = 0; i < b.len; i++){
c.d[i] -= b.d[i];
if (c.d[i] < 0) c.d[i]+=10, c.d[i+1]--;
}
while (c.d[i] < 0) c.d[i++]+=10, c.d[i]--;
c.clean();
return c;
}
bign operator * (const bign& b)const{
int i, j; bign c; c.len = len + b.len;
for(j = 0; j < b.len; j++) for(i = 0; i < len; i++)
c.d[i+j] += d[i] * b.d[j];
for(i = 0; i < c.len-1; i++)
c.d[i+1] += c.d[i]/10, c.d[i] %= 10;
c.clean();
return c;
}
bign operator / (const bign& b){
int i, j;
bign c = *this, a = 0;
for (i = len - 1; i >= 0; i--)
{
a = a*10 + d[i];
for (j = 0; j < 10; j++) if (a < b*(j+1)) break;
c.d[i] = j;
a = a - b*j;
}
c.clean();
return c;
}
bign operator % (const bign& b){
int i, j;
bign a = 0;
for (i = len - 1; i >= 0; i--)
{
a = a*10 + d[i];
for (j = 0; j < 10; j++) if (a < b*(j+1)) break;
a = a - b*j;
}
return a;
}
bign operator += (const bign& b){
*this = *this + b;
return *this;
}
bool operator <(const bign& b) const{
if(len != b.len) return len < b.len;
for(int i = len-1; i >= 0; i--)
if(d[i] != b.d[i]) return d[i] < b.d[i];
return false;
}
bool operator >(const bign& b) const{return b < *this;}
bool operator<=(const bign& b) const{return !(b < *this);}
bool operator>=(const bign& b) const{return !(*this < b);}
bool operator!=(const bign& b) const{return b < *this || *this < b;}
bool operator==(const bign& b) const{return !(b < *this) && !(b > *this);}
string str() const{
char s[maxn]={};
for(int i = 0; i < len; i++) s[len-1-i] = d[i]+'0';
return s;
}
};
istream& operator >> (istream& in, bign& x){
string s;
in >> s;
x = s.c_str();
return in;
}
ostream& operator << (ostream& out, const bign& x){
out << x.str();
return out;
}
#define ll bign
ll f[55][55],a[55];
int n;
int main(){
cin>>n;
for(int i=1;i<=n;i+=1) cin>>a[i];
memset(f,63,sizeof(f));
for(int i=1;i<=n;i++) f[i][i+1]=0;
for(int L=2;L<=n-1;L++){
for(int i=1;i<=n-L;i++){
int j=i+L;
for(int k=i+1;k<=j-1;k++){
f[i][j]=min(f[i][k]+f[k][j]+a[i]*a[j]*a[k],f[i][j]);
}
}
}
cout<<f[1][n];putchar('\n');
return 0;
}
//f[i][j]=min{f[i][k]+f[k][j]+a[i]*a[j]*a[k]}(0<i<k<j<=n)
//f[i][j]=inf
//f[i][i+1]=0;
//end:f[1][n]
//Time:O(n^3)
#10153. 「一本通 5.2 例 1」二叉苹果树
题意
有一棵二叉苹果树,如果数字有分叉,一定是分两叉,即没有只有一个儿子的节点。这棵树共 $N$ 个节点,标号 $1$ 至 $N$,树根编号一定为 $1$。
我们用一根树枝两端连接的节点编号描述一根树枝的位置。一棵有四根树枝的苹果树,因为树枝太多了,需要剪枝。但是一些树枝上长有苹果,给定需要保留的树枝数量,求最多能留住多少苹果。 
思路
设$f[i][j]$表示以i为根节点,保留j个节点的最大苹果数量
$$f[i][j]=max{f[l[i]][k]+f[r[i]][j-k-1]+a[i]}(0<=k<=j-1)$$
$$f[i][j]=0(0<i<=n,0<=j<=Q+1)$$
$$f[i][j]=ai$$
$$Answer:f[1][Q+1]$$
#include<bits/stdc++.h>
#define ll long long
using namespace std;
inline ll read(){
char ch=getchar();ll res=0,f=1;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9') res=res*10+ch-'0',ch=getchar();
return res*f;
}
inline void write(ll x){
if(x<0) putchar('-'),x=-x;
if(x<10) putchar(x+'0');
else{
write(x/10);
putchar(x%10+'0');
}
}
ll n,Q,f[110][110],a[110],l[110],r[110],mp[110][110];
void MakeTree(int x){
for(int i=1;i<=n;i++){
if(mp[x][i]!=-1){
l[x]=i;a[i]=mp[x][i];
mp[x][i]=mp[i][x]=-1;
MakeTree(i);
break;
}
}//Make Left Son
for(int i=1;i<=n;i++){
if(mp[x][i]!=-1){
r[x]=i;a[i]=mp[x][i];
mp[x][i]=mp[i][x]=-1;
MakeTree(i);
break;
}
}//Make Right Son
}
int DP(int x,int j){
if(j==0){f[x][j]=0;return 0;}
if((!l[x])&&(!r[x])){f[x][j]=a[x];return a[x];}
if(f[x][j]>0) return f[x][j];
for(int k=0;k<j;k++) f[x][j]=max(f[x][j],DP(l[x],k)+DP(r[x],j-k-1)+a[x]);
return f[x][j];
}
int main(){
n=read();Q=read();Q++;
memset(mp,-1,sizeof(mp));
for(int i=1;i<=n-1;i++){
int x=read(),y=read(),z=read();
mp[y][x]=mp[x][y]=z;
}
MakeTree(1);
write(DP(1,Q));putchar('\n');
/*
cout<<"-----------------------------------"<<endl;
for(int i=1;i<=n;i++){
cout<<"Node "<<i<<":\n";
cout<<"Left Son:"<<l[i]<<" Right Son:"<<r[i]<<endl;
cout<<"Val:"<<a[i]<<endl;
cout<<"DP :\n";
for(int j=0;j<=Q;j++){
cout<<"Has "<<j<<":"<<f[i][j]<<endl;
}
cout<<endl;
}
*/
return 0;
}
//设f[i][j]表示以i为根节点,保留j个节点的最大苹果数量
//f[i][j]=max{f[l[i]][k]+f[r[i]][j-k-1]+a[i]}(0<=k<=j-1)
//f[i][j]=0(0<i<=n,0<=j<=Q+1)
//f[i][j]=a[i](j!=0&&l[i]==0&&r[i]==0)
//Answer:f[1][Q+1]
/*
Sample Input:
5 2
1 3 1
1 4 10
2 3 20
3 5 20
Sample Output:
21
*/
#10154. 「一本通 5.2 例 2」选课
题意
有很多课程,但部分课程有先修课。学生不可能学完大学开设的所有课程,因此必须在入学时选定自己要学的课程。每个学生可选课程的总数是给定的。请找出一种选课方案使得你能得到的学分最多,并满足先修课优先的原则。假定课程间不存在时间上的冲突。
思路
瞎搞树形DP。
发现这是背包。
还是分组背包。(^▽^)
于是就愉快地解决了。
设$f[x][t]$表示以x为根节点的子树中选t门课能够获得的最高学分。(所以说是背包问题嘛) $$Answer:f[0][m]$$
#include<algorithm>
#include<bitset>
#include<complex>
#include<deque>
#include<exception>
#include<fstream>
#include<functional>
#include<iomanip>
#include<ios>
#include<iosfwd>
#include<iostream>
#include<istream>
#include<iterator>
#include<limits>
#include<list>
#include<locale>
#include<map>
#include<memory>
#include<new>
#include<numeric>
#include<ostream>
#include<queue>
#include<set>
#include<sstream>
#include<stack>
#include<stdexcept>
#include<streambuf>
#include<string>
#include<typeinfo>
#include<utility>
#include<valarray>
#include<vector>
#include<cstring>
#include<cmath>
#define ll long long
#define eps 1e-4
using namespace std;
inline int read(){
int ret=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9') {if (ch=='-') f=-f;ch=getchar();}
while (ch>='0'&&ch<='9') ret=ret*10+ch-'0',ch=getchar();
return ret*f;
}
inline void write(int zx){
if(zx<0){zx=-zx;putchar('-');}
if(zx<10) putchar(zx+'0');
else{
write(zx/10);
putchar(zx%10+'0');
}
}
int n,m,fir[310],nxt[310];
int s[310],w[310],f[310][310];
int DP(int x){
if(fir[x]==-1) return 0;
int sum=0;
for(int i=fir[x];i!=-1;i=nxt[i]){
int tmp=DP(i);
sum+=tmp+1;
for(int j=sum;j>=0;j--)
for(int k=0;k<=tmp;k++)
if(j-k-1>=0) f[x][j]=max(f[x][j],f[x][j-k-1]+f[i][k]);
}
return sum;
}
int main(){
n=read();m=read();
memset(fir,-1,sizeof(fir));
for(int i=1;i<=n;i++){
s[i]=read();w[i]=read();
nxt[i]=fir[s[i]];
fir[s[i]]=i;
}
for(int i=1;i<=n;i++) f[i][0]=w[i];
f[0][0]=0;
DP(0);
write(f[0][m]);
putchar('\n');
return 0;
}
#10155. 「一本通 5.2 例 3」数字转换
题意
如果一个数 $x$ 的约数和 $y$ (不包括他本身)比他本身小,那么 $x$ 可以变成 $y$,$y$ 也可以变成 $x$。例如 $4$ 可以变为 $3$,$1$ 可以变为 $7$。限定所有数字变换在不超过 $n$ 的正整数范围内进行,求不断进行数字变换且不出现重复数字的最多变换步数。
思路
求树的最长链
设$d1[i]$为以$i$为根的子树中,i到叶子节点距离最大值
设$d2[i]$为以$i$为根的子树中,i的叶子节点距离次大值(除了最大值所在的子树)
若j为i的儿子,那么:
- 若$d1[j]+dis[i][j]>d1[i]$,则$d2[i]=d1[i];d1[i]=d2[j]=dis[i][j];$
- 否则,若$d1[j]+dis[i][j]>d2[i]$,则$d2[i]=d1[j]+dis[i][j]; $
最后扫描所有节点,最长链=max{d1[i]+d2[i]}
#include<algorithm>
#include<bitset>
#include<complex>
#include<deque>
#include<exception>
#include<fstream>
#include<functional>
#include<iomanip>
#include<ios>
#include<iosfwd>
#include<iostream>
#include<istream>
#include<iterator>
#include<limits>
#include<list>
#include<locale>
#include<map>
#include<memory>
#include<new>
#include<numeric>
#include<ostream>
#include<queue>
#include<set>
#include<sstream>
#include<stack>
#include<stdexcept>
#include<streambuf>
#include<string>
#include<typeinfo>
#include<utility>
#include<valarray>
#include<vector>
#include<cstring>
#include<cmath>
#define ll long long
#define eps 1e-4
using namespace std;
//priority_queue<int,vector<int>,greater<int> > q1;
//priority_queue<int> q2;
//set<int> s;
//list<int> l;
//map<int> mp;
inline int read(){
int ret=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9') {if (ch=='-') f=-f;ch=getchar();}
while (ch>='0'&&ch<='9') ret=ret*10+ch-'0',ch=getchar();
return ret*f;
}
inline void write(int zx){
if(zx<0){zx=-zx;putchar('-');}
if(zx<10) putchar(zx+'0');
else{
write(zx/10);
putchar(zx%10+'0');
}
}
int sum[500001],n,d1[500001],d2[500001],ans;
void Pri(){
for(int i=1;i<=n;i++){
for(int j=2;j<=n/i;j++){
if(i*j>n) break;
sum[i*j]+=i;
}
}
}
void dp(){
for(int i=n;i>=1;i--){
if(sum[i]<i){
if(d1[i]+1>d1[sum[i]]){
d2[sum[i]]=d1[sum[i]];
d1[sum[i]]=d1[i]+1;
}else if(d1[i]+1>d2[sum[i]]) d2[sum[i]]=d1[i]+1;
}
}
}
int main(){
n=read();
Pri();
dp();
for(int i=1;i<=n;i++) ans=max(ans,d1[i]+d2[i]);
write(ans);putchar('\n');
return 0;
}
来源:oschina
链接:https://my.oschina.net/u/4413093/blog/3662251