单级CIC滤波器理论与设计
项目简述
工欲善其事必先利其器,信号处理有强大的理论支撑。若是没有掌握这些理论,只是随便找一些符合要求的代码,那么自己很难更近一步。而且算法本身就是FPGA工程师的难点,而不是硬件逻辑。所以,本篇文章我们将进行CIC抗混叠滤波器的设计,这在信号处理中具有及其重要的地位。接下来,我们将从理论与FPGA设计的两个角度来讲解CIC的设计
多速率信号处理
这个概念是相对于单速率(Single Rate)信号处理而言的。单速率 是指整个信号处理流程中只有一种数据速率;多速率 是指系统中存在多个数据速率。使用多速率信号处理可以节省存储空间、减少通信数据量、减少运算量、减轻设计难度。
很明显从字面意思上可以理解,多采样率嘛,就是有多个采样率呗。前面所说的FIR,IIR滤波器都是只有一个采样频率,是固定不变的采样率,然而有些情况下需要不同采样频率下的信号,具体例子我们将以数字下变频(DDC)为例来进行讲解。
按照传统的速率转换理论,我们要实现采样速率的转换,可以这样做,假如有一个有用的正弦波模拟信号,AD采样速率是f1,现在我需要用到的是采样频率是f2的信号,传统做法是将这个经过f1采样后的信号进行DA转换,再将转换后的模拟信号进行以f2采样频率的抽样,得到采样率为f2的数字信号,至此完成采样频率的转换。所以我们引入了更好的抽取与内插方法。
比如在DDC(数字下变频)系统中,前级需要很高的采样率fs确保ADC采集到信号的信噪比;而在去载波并提取出低频的基带信号后,信号有效带宽已经很小,此时可以满足要求的采样率也远远低于fs,如果不进行数据速率转换的处理,会造成许多资源的浪费和设计上的困难:
多速率信号处理 主要包括 数据速率的转换 和 LPF的设计 两个过程。数据速率的转换包括 抽取(Decimation,降低采样率) 和 内插(interpolation,提高采样率) 。抽取/内插时应保证信号的有效频带内没有频谱混叠,因此需要完成LPF的设计,常用的有 多速率FIR滤波器、CIC滤波器、HB滤波器。
从上面的文章中,我们可以看出多速率滤波器最重要的也就是***抽取***与***内插***两个操作。
抽取
当需要降低采样率时,输入信号数据每隔D-1个取一个,取出的数据依次排序,这个过程称作D倍抽取,采样率变为原来的1/D。但是我们需要确保抽取之后的采样率仍然可以满足Nyquist采样定理,否则会造成频谱的混叠。当然由于ADC的转换也会在整个频段内引入白噪声,因此在抽取前还是需要加入***抗混叠滤波器***。如下图所示:
上面是抽取的主要操作,也是绝大多数FPGA工程师进行的操作,但是却不明白其中的原理。接下来我们将从信号处理的角度解释上面两点:
1、为什么一定要保证抽取后满足奈奎斯特抽样定理。
2、为什么要先经过抗混叠滤波器。
先来总体来解释一下***抽取***的含义:前面不是说,一个有用的正弦波模拟信号经采样频率为f1的抽样信号抽样后得到了数字信号,很明显这个数字信号序列是在f1频率下得到的,现在,假如我隔几个点抽取一个信号,比如就是5吧,我隔5个点抽取一个信号,是不是就是相当于我采用了1/5倍f1的采样频率对模拟信号进行采样了?所以,抽取的过程就是降低抽样率的过程,但是我们知道,这是在时域的抽样,时域的抽样等于信号在频域波形的周期延拓(信号系统中的公式),周期就是采样频率,所以,为了避免在频域发生频谱混叠,抽样定理也是我们要考虑的因素
下面来具体来介绍: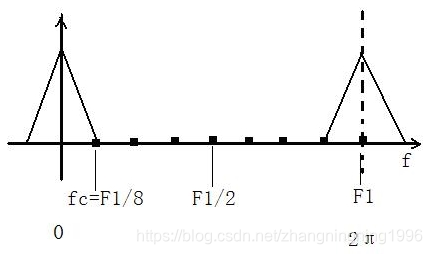
如上图所示,假如上面就是某一有用信号经采样频率f1抽样得到的频谱,假设这时候的采样频率为8Khz,可以通过数格子得到,从0到F1处有8个空格,每个空格代表1Khz,有些朋友可能会问,这不是在数字频域吗,单位不是π吗,哪来的hz?是的,这里是数字频域,采样频率F1处对应的是2π,这里只是为了好解释,我们用模拟频率来对应数字频率(如果这里不懂的话需要恶补信号系统与数字信号处理的知识)。
下图就是对信号进行了1/5倍的F1采样频率抽取,可见,由于发生了频谱混叠现象,因为1/5倍的F1是1600hz,而信号的频带是1000hz,不满足抽样定理,导致发生了***频谱混叠***,所以,为了避免发生这种情况,除了要满足抽样定理之外,即抽样倍数不能太高,我们还需要把信号的频带设置在F1/2以下,才能确保信号不发生频谱混叠,因此,我们需要在抽取之前加一个低通滤波器,书上叫做***抗混叠低通滤波***器,用来限制信号的频带,然后再进行抽取。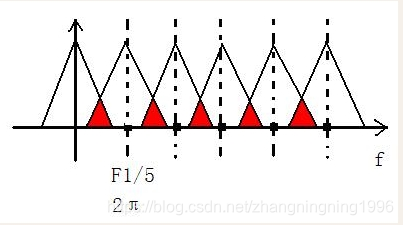
这样的话我们来算一下,低通滤波器的截止频率就是1/2倍的经抽取后的采样速率,即fc = 1/2 * (F1/M) ,M是抽取倍数。而1/2*F1对应的数域频率是π,因此我们得出,抗混叠低通滤波器的截止频率是π/M。
内插
当需要提高采样率时,在两个相邻的数据之间插入***I-1个零值***,再进行低通滤波,这个过程称作 I倍内插 ,采样率变为原来的I倍。只要LPF的通带为信号的有效带宽,即使插值时只插入零值点(没有插入采样值的点),也可以达到I倍内插的效果。经过插值后的信号由DAC输出会引入更小的高频噪声。如下图所示:

抽取的过程是降低采样率的过程,那么***插值***的过程当然就是***提高采样率***的过程。大体的思路可以这么理解,我们将经f1抽样下得到的数字信号的每两个点之间进行插值,插入的值是0,插值之后,信号在单位时间内的采样点数增多,当然也就是采样速率的提升,采样速率提升后我们知道,那么信 号的频谱的周期数就会增加: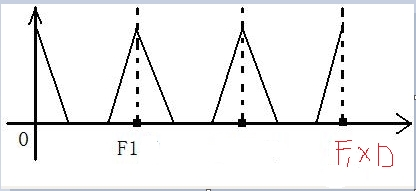
信号系统学的好的同学可以试着推导一下上面的频谱变化,相信不是太难。
需要注意的一点就是,插值前后,我们只是在时域信号***中间插入了D-1个零值***,仅仅是改变了采样率,并没有改变信号的信息,因此,在频域,信号频谱的形状是不会改变的,改变的仅仅是模拟频率与数字频率的对应,如上图,F1是插值之前信号的抽样频率,插值之后,信号频谱的形状不变,抽样频率成了**F1D,D是插值倍数***。如果我们直接用F1D倍的采样率采信号,得到的频谱会发现,就不会有中间两个波形,因此,这两个波形是多余的,书上叫做是镜像频谱*。既然是多余的,我们就可以将***它用一个低通滤波器滤掉,这样的低通滤波器,就叫做镜像低通滤波器***。这样我们来计算一下镜像低通滤波器的截止频率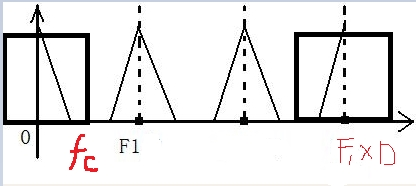
根据上面这张图我们可以求出镜像低通滤波器的截止频率,可以看到,fc = 1/2 F1,这里我们假设,内插之后的采样频率为F2 =F1D,那么,fc =1/2*(F2/D),而1/2F2对应的是π,注意,这里是1/2F2对应π,不是1/2*F1了,因为这已经是插值之后采样率增加之后的频谱了,所以我们得出,镜像低通滤波器的截止频率为:π/D
分数倍抽取与内插
上面抽取和内插实现的都是整数倍数据速率的转换。而实际设计中遇到的更多不会是整数倍关系。可以使用先内插、再抽取的方式完成采样率为有理数比值的数据速率转换,且可以共用一个LPF,截止频率选取二者的最小带宽即可。如下图所示:

根据前面抽取与内插的介绍我们知道了,内插的过程是先进行内插处理,再通过镜像低通滤波器,抽取的过程就是先进行抗混叠低通滤波,再进行抽取,我们可以看出来,假如我们想进行分数倍抽取,比如***我要进行3/5倍抽取,就可以先进行3倍内插,再进行5倍抽取,这样就可以实现分数倍抽取***。
再来看一下,当进行分数倍抽取与内插的时候,镜像低通滤波器和抗混叠低通滤波器是连在一起的,因此,我们可以将这两个滤波器合二为一,截止频率取两个滤波器截止频率的最小值就可以了。
上面关于数据的抽取与内插的知识已经介绍完毕,如果有哪里不懂,可以查阅书本知识。从这篇文章我们也可以看出来数字***信号处理理论知识***的重要性。如果上大学的同学看到这篇文章,这里劝诫一定学好基础理论,否则只能做个调参侠。
CIC滤波器
CIC滤波器 是无线通信的常用模块,一般用于 数字下变频(DDC)和数字上变频(DUC)系统。CIC滤波器结构简单,没有乘法器,只有加法器、积分器和寄存器,可以实现高速滤波,***常用在输入采样率最高的第一级。从上面可以看出来CIC滤波器的优点:CIC(Cascaded Integrator Comb)积分梳状与其他多速率FIR滤波器滤波器***运算速度快、占用资源少C、工作频率高(因为CIC只使用加法器、减法器和寄存器),在多速率信号处理系统中应用更广泛。
CIC滤波器理论推导
单级CICI滤波器
CIC滤波器包括两个基本组成部分:积分部分和梳妆部分,如图所示:
积分部分的积分器是单极点的IIR滤波器,并且反馈系数为1,状态方程为:
y ( n ) = y ( n − 1 ) + x ( n ) y(n)=y(n−1)+x(n) y(n)=y(n−1)+x(n)
上述的积分器也可以看做是累加器。根据Z变换,积分器的传输函数为:
H 1 ( z ) = 1 1 − z − 1 H_1(z)=\frac{1}{1−z^{-1}} H1(z)=1−z−11
梳妆器是一份FIR滤波器,其状态方程为:
y ( n ) = x ( n − 1 ) − x ( n − D M ) y(n)=x(n−1)-x(n−DM) y(n)=x(n−1)−x(n−DM)
式中,D是设计参数,称为微分延迟,其传输函数为:
H c ( z ) = 1 − z − D M H_c(z)=1−z^{-DM} Hc(z)=1−z−DM
那么:单级CIC滤波器的传递函数为:
H ( z ) = 1 1 − z − 1 ( 1 − z D M ) H(z)=\frac{1}{1−z^{-1}}(1−z^{DM}) H(z)=1−z−11(1−zDM)
令 z = e j w z=e_{jw} z=ejw,带入上式,可以得到传递函数的幅频响应为:
CIC滤波器的幅频响应特性如图所示,其中[0,2π/DM]为主瓣,其他的区间称为旁瓣。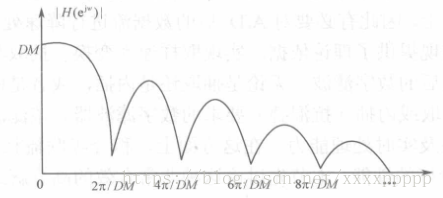
从幅频响应特性可以看到,主瓣的最大值为DM(在w=0时),旁瓣的最大值在 w = 3 π / D M w=3π/DM w=3π/DM处 取得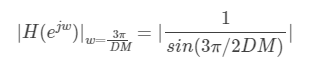
它与主瓣电平的比值为: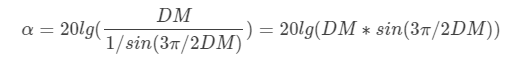
根据在θ在0~45°时, θ ≈ s i n θ θ≈sinθ θ≈sinθ,可得:
α = 20 l g ( 3 π 2 ) = 13.36 d B α=20lg(\frac{3π}{2})=13.36dB α=20lg(23π)=13.36dB
可见单级CIC滤波器的旁瓣电平较大,阻带衰减较差。为降低旁瓣电平,可以采用多级CIC滤波器级联办法来实现。
多级CICI滤波器
根据前面可知,单级CIC滤波器的第一旁瓣电平衰减固定为13.46dB,且与滤波器的阶数无关。这个值不满足通常的阻带衰减要求,解决方法就是通过级联CIC滤波器来达到更大的阻带衰减。事实上实际应用中采用的都是多级CIC滤波器。
一个N级CIC抽取滤波器系统传递函数为:
H ( z ) = ( 1 − z − D M 1 − z − 1 ) N H(z)=(\frac{1−z^{−DM}}{1−z^{−1}})^N H(z)=(1−z−11−z−DM)N
在N级级联时,阻带衰减为单级衰减的N倍,即13.46×N(dB)。
但是在阻带衰减的情况下也带来一系列的问题:
1、要同时满足通带容限跟阻带容限的误差的CIC滤波器实现起来比较困难,因为要想阻带衰减大,就要增大滤波器级数,但是会导致通带容限增大。
2、如果要实现这样的滤波器,只有当有用信号的频带相对于采样信号的速率很小时才能设计出符合要求的滤波器,这样的话通带衰减较大的情况下也对有用信号影响较小。
3、有用信号的频带相对于采样信号的速率很小也就是意味着信号的采样率很高,所以,CIC滤波器适合应用在多速率信号处理的前端,作为抗混叠滤波器来用,或者是作为后端的抗混叠插值滤波器。
CIC滤波器的FPGA实现
上面我们已经对CIC的主要原理进行了讲述。其实CIC滤波器***本质***上就是一个***简单的低通滤波器***,只是方便与抽取与内插联系起来,下面我们将给出源代码供大家学习:
CIC抽取滤波器代码
使用50MHz采样率对0.25MHz的信号进行采样,由五阶CIC滤波器进行5倍抽取,将采样率降至10MHz。这里我们直接给出CIC抽取滤波器代码,
cic模块:
`timescale 1ns / 1ps
// *********************************************************************************
// Project Name : OSXXXX
// Author : zhangningning
// Email : nnzhang1996@foxmail.com
// Website :
// Module Name : cic.v
// Create Time : 2020-04-24 15:08:16
// Editor : sublime text3, tab size (4)
// CopyRight(c) : All Rights Reserved
//
// *********************************************************************************
// Modification History:
// Date By Version Change Description
// -----------------------------------------------------------------------
// XXXX zhangningning 1.0 Original
//
// *********************************************************************************
module cic(
//System Interfaces
input sclk ,
input rst_n ,
//Communication Interfaces
input rvalid ,
input [ 9:0] din ,
output reg tvalid ,
output reg [12:0] dout
);
//========================================================================================\
//**************Define Parameter and Internal Signals**********************************
//========================================================================================/
reg [ 2:0] cnt ;
reg [12:0] sum ;
wire [12:0] din_x ;
//========================================================================================\
//************** Main Code **********************************
//========================================================================================/
assign din_x = {{3{din[9]}},din};
always @(posedge sclk or negedge rst_n)
if(rst_n == 1'b0)
cnt <= 3'd0;
else if(rvalid == 1'b1 && cnt == 'd4)
cnt <= 3'd0;
else if(rvalid == 1'b1)
cnt <= cnt + 1'b1;
else
cnt <= cnt;
always @(posedge sclk or negedge rst_n)
if(rst_n == 1'b0)
sum <= 13'd0;
else if(rvalid == 1'b1 && cnt == 'd4)
sum <= din_x;
else if(rvalid == 1'b1)
sum <= sum + din_x;
else
sum <= sum;
always @(posedge sclk or negedge rst_n)
if(rst_n == 1'b0)
dout <= 13'd0;
else if(rvalid == 1'b1 && cnt == 'd4)
dout <= sum;
else
dout <= dout;
always @(posedge sclk or negedge rst_n)
if(rst_n == 1'b0)
tvalid <= 1'b0;
else if(rvalid == 1'b1 && cnt == 'd4)
tvalid <= 1'b1;
else
tvalid <= 1'b0;
endmodule
有不少同学会问吗,这不就是对输出的5个数据求了一次平均,咋么能说是CIC抽取滤波器呢。因为当梳状滤波器的阶数与抽取的的数目相同时,可以在积分器之后先抽取再经过梳状滤波器。然后经过稍微化简便可以成为上述形式。这也原理被称为***Noble恒等式。***I
在抽取的过程中,一般是信号先经过抗混叠低通滤波器进行滤波,来避免频谱混叠现象的发生,然后再进行抽取处理,但是我们可以利用Noble恒等式,先对信号进行抽取,再对其进行滤波。这些知识再多级CIC滤波器应用中尤其明显,我们将在下一篇文章中进行进一步的讲解
CIC抽取滤波器测试代码
关于CIC抽取滤波器的代码,我们使用了DDS来产生采样率50MHz、频率0.25MHz的正弦波。代码如下:
tb模块:
`timescale 1ns / 1ps
// *********************************************************************************
// Project Name : OSXXXX
// Author : zhangningning
// Email : nnzhang1996@foxmail.com
// Website :
// Module Name : tb.v
// Create Time : 2020-04-24 16:00:12
// Editor : sublime text3, tab size (4)
// CopyRight(c) : All Rights Reserved
//
// *********************************************************************************
// Modification History:
// Date By Version Change Description
// -----------------------------------------------------------------------
// XXXX zhangningning 1.0 Original
//
// *********************************************************************************
module tb();
reg sclk ;
reg rst_n ;
wire rvalid ;
wire [ 7:0] din ;
wire tvalid ;
wire [12:0] dout ;
initial begin
sclk = 1'b0;
rst_n <= 1'b0;
#(1000);
rst_n <= 1'b1;
end
always #(10) sclk = ~sclk;
dds_compiler_0 dds_compiler_0_inst (
.aclk (sclk ), // input wire aclk
.m_axis_data_tvalid (rvalid ), // output wire m_axis_data_tvalid
.m_axis_data_tdata (din ) // output wire [7 : 0] m_axis_data_tdata
);
cic cic_inst(
//System Interfaces
.sclk (sclk ),
.rst_n (rst_n ),
//Communication Interfaces
.rvalid (rvalid ),
.din ({{2{din[7]}},din} ),
.tvalid (tvalid ),
.dout (dout )
);
endmodule
CIC抽取滤波器仿真结果
上述的仿真结果如下: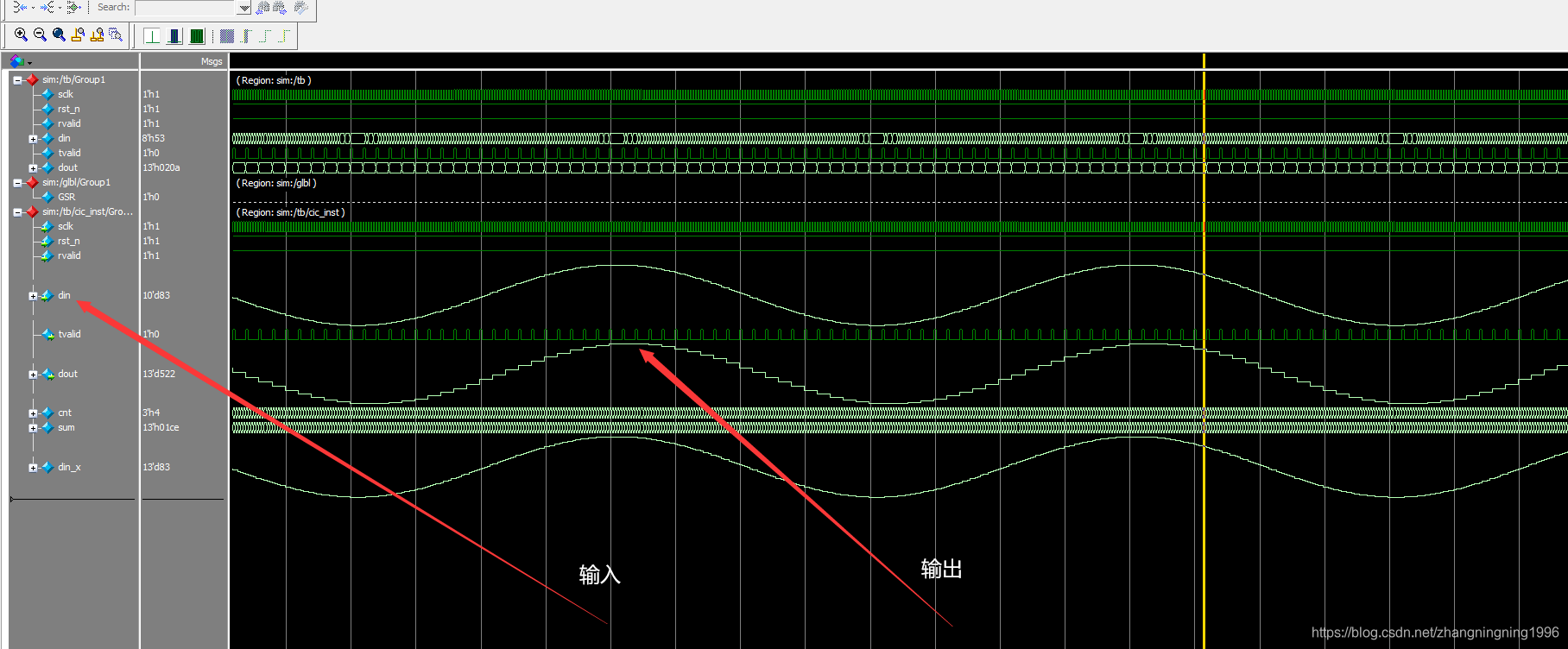
从上面我们很明显看出我们成功实现了正弦波的抽取。从而验证了我们实验的正确性。
CIC内插滤波器代码
关于CIC抽取滤波器的代码,我们使用了DDS来产生采样率50MHz、频率0.25MHz的正弦波,然后经过10倍抽取使得采样率降为5MHz;再经过10倍插值,最后经过100阶的CIC滤波器检验其内插效果。代码如下:
CIC_inter模块:
`timescale 1ns / 1ps
// *********************************************************************************
// Project Name : OSXXXX
// Author : zhangningning
// Email : nnzhang1996@foxmail.com
// Website :
// Module Name : CIC_inter.v
// Create Time : 2020-04-24 20:20:56
// Editor : sublime text3, tab size (4)
// CopyRight(c) : All Rights Reserved
//
// *********************************************************************************
// Modification History:
// Date By Version Change Description
// -----------------------------------------------------------------------
// XXXX zhangningning 1.0 Original
//
// *********************************************************************************
module CIC_inter(
//System Interfaces
input sclk ,
input rst_n ,
//Communication Interfaces
input rvalid ,
input [12:0] din ,
output reg tvalid ,
output wire [19:0] dout
);
//========================================================================================\
//**************Define Parameter and Internal Signals**********************************
//========================================================================================/
reg [ 9:0] cnt ;
wire [19:0] din_x ;
wire [19:0] data ;
reg data_valid ;
reg [ 9:0] cnt_cic ;
reg [19:0] sum ;
//========================================================================================\
//************** Main Code **********************************
//========================================================================================/
assign din_x = {{7{din[12]}},din};
assign data = din_x;
assign dout = sum;
always @(posedge sclk or negedge rst_n)
if(rst_n == 1'b0)
cnt <= 10'd0;
else if(cnt == 10'd0 && rvalid == 1'b1)
cnt <= cnt + 1'b1;
else if(cnt > 0 && cnt == 'd9)
cnt <= 10'd0;
else if(cnt > 0)
cnt <= cnt + 1'b1;
else
cnt <= 10'd0;
always @(posedge sclk or negedge rst_n)
if(rst_n == 1'b0)
data_valid <= 1'b0;
else if(cnt == 10'd0 && rvalid == 1'b1)
data_valid <= 1'b1;
else if(cnt > 0)
data_valid <= 1'b1;
else
data_valid <= 1'b0;
always @(posedge sclk or negedge rst_n)
if(rst_n == 1'b0)
cnt_cic <= 10'd0;
else if(data_valid == 1'b1 && cnt_cic == 'd99)
cnt_cic <= 10'd0;
else if(data_valid == 1'b1)
cnt_cic <= cnt_cic + 1'b1;
else
cnt_cic <= cnt_cic;
always @(posedge sclk or negedge rst_n)
if(rst_n == 1'b0)
sum <= 16'd0;
else if(data_valid == 1'b1 && cnt_cic == 'd99)
sum <= data;
else if(data_valid == 1'b1)
sum <= sum + data;
else
sum <= sum;
always @(posedge sclk or negedge rst_n)
if(rst_n == 1'b0)
tvalid <= 1'b0;
else if(data_valid == 1'b1)
tvalid <= 1'b1;
else
tvalid <= 1'b0;
endmodule
cic模块:
`timescale 1ns / 1ps
// *********************************************************************************
// Project Name : OSXXXX
// Author : zhangningning
// Email : nnzhang1996@foxmail.com
// Website :
// Module Name : cic.v
// Create Time : 2020-04-24 15:08:16
// Editor : sublime text3, tab size (4)
// CopyRight(c) : All Rights Reserved
//
// *********************************************************************************
// Modification History:
// Date By Version Change Description
// -----------------------------------------------------------------------
// XXXX zhangningning 1.0 Original
//
// *********************************************************************************
module cic(
//System Interfaces
input sclk ,
input rst_n ,
//Communication Interfaces
input rvalid ,
input [ 9:0] din ,
output reg tvalid ,
output reg [12:0] dout
);
//========================================================================================\
//**************Define Parameter and Internal Signals**********************************
//========================================================================================/
reg [ 9:0] cnt ;
reg [12:0] sum ;
wire [12:0] din_x ;
//========================================================================================\
//************** Main Code **********************************
//========================================================================================/
assign din_x = {{3{din[9]}},din};
always @(posedge sclk or negedge rst_n)
if(rst_n == 1'b0)
cnt <= 10'd0;
else if(rvalid == 1'b1 && cnt == 'd9)
cnt <= 10'd0;
else if(rvalid == 1'b1)
cnt <= cnt + 1'b1;
else
cnt <= cnt;
always @(posedge sclk or negedge rst_n)
if(rst_n == 1'b0)
sum <= 13'd0;
else if(rvalid == 1'b1 && cnt == 'd9)
sum <= din_x;
else if(rvalid == 1'b1)
sum <= sum + din_x;
else
sum <= sum;
always @(posedge sclk or negedge rst_n)
if(rst_n == 1'b0)
dout <= 13'd0;
else if(rvalid == 1'b1 && cnt == 'd9)
dout <= sum;
else
dout <= dout;
always @(posedge sclk or negedge rst_n)
if(rst_n == 1'b0)
tvalid <= 1'b0;
else if(rvalid == 1'b1 && cnt == 'd9)
tvalid <= 1'b1;
else
tvalid <= 1'b0;
endmodule
CIC内插滤波器测试代码
tb模块:
`timescale 1ns / 1ps
// *********************************************************************************
// Project Name : OSXXXX
// Author : zhangningning
// Email : nnzhang1996@foxmail.com
// Website :
// Module Name : tb.v
// Create Time : 2020-04-24 16:00:12
// Editor : sublime text3, tab size (4)
// CopyRight(c) : All Rights Reserved
//
// *********************************************************************************
// Modification History:
// Date By Version Change Description
// -----------------------------------------------------------------------
// XXXX zhangningning 1.0 Original
//
// *********************************************************************************
module tb();
reg sclk ;
reg rst_n ;
wire rvalid ;
wire [ 7:0] din ;
wire tvalid ;
wire [12:0] dout ;
wire [15:0] CIC_inter_data ;
wire CIC_inter_tvalid;
initial begin
sclk = 1'b0;
rst_n <= 1'b0;
#(1000);
rst_n <= 1'b1;
end
always #(10) sclk = ~sclk;
dds_compiler_0 dds_compiler_0_inst (
.aclk (sclk ), // input wire aclk
.m_axis_data_tvalid (rvalid ), // output wire m_axis_data_tvalid
.m_axis_data_tdata (din ) // output wire [7 : 0] m_axis_data_tdata
);
cic cic_inst(
//System Interfaces
.sclk (sclk ),
.rst_n (rst_n ),
//Communication Interfaces
.rvalid (rvalid ),
.din ({{2{din[7]}},din} ),
.tvalid (tvalid ),
.dout (dout )
);
CIC_inter CIC_inter_inst(
//System Interfaces
.sclk (sclk ),
.rst_n (rst_n ),
//Communication Interfaces
.rvalid (tvalid ),
.din (dout ),
.tvalid (CIC_inter_tvalid ),
.dout (CIC_inter_data )
);
endmodule
CIC内插滤波器仿真结果
将工程进行Modelsim仿真,结果如下: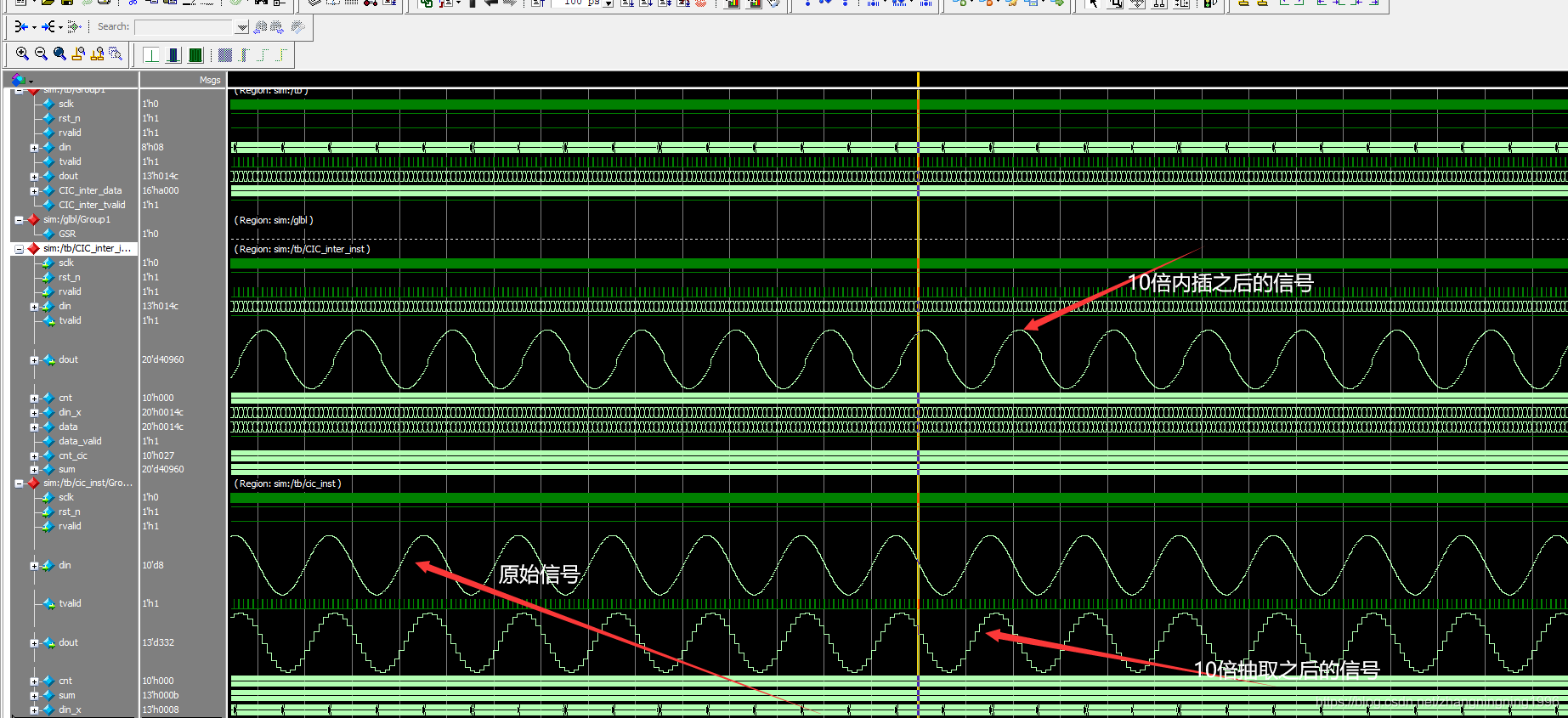
从上面的结果可以看出内插结果正确,但是由于单级CIC滤波器的阻带衰减太低,所以在实际工程中一般都是使用多级CIC滤波器进行滤波,详细的情况将在我们接下来的博客中进行论述。
参考文献
[1]、FPGADesigner——CSDN博主
[2]、长弓的坚持——CSDN博主
[3]、行州人——CSDN博主
总结
在查找一些资料的时候,发现一些博主只给出部分代码,其实这样别人根本看不懂,只有给出整个工程代码才易于知识的传播。创作不易,认为文章有帮助的同学们可以关注、点赞、转发支持。为行业贡献及其微小的一部分。或者对文章有什么看法或者需要更近一步交流的同学,可以加入下面的群:
来源:oschina
链接:https://my.oschina.net/u/4310671/blog/4253849