如果您觉得本文有用,可以在微博上关注我,每周我都会在微博上发布新博客发表的通知,我的微博
###深度优先搜索
####介绍
如果您觉得这篇文章排版不舒服,请到我的微盘下载pdf:搜索算法-深度优先搜索
深度优先搜索是一种用来遍历或者搜索树(TREE)或图(GRAPH)结构的算法。搜索开始于某个根节点(从图中选取某个节点),然后在开始回溯前尽可能远地探索到这一支的终点。
对于DFS的实际应用程序来说,DFS常常因为要搜索的图的某一条搜索路径太长(甚至是无限的)而陷入性能瓶颈,所以我们经常制定DFS只能搜索到某个深度,
如果用一个图来代表深度优先搜索的过程,即如下图:

####深度优先遍历的伪码实现
相应的伪码实现在《算法导论》这本书中有讲解,书中用的方法十分巧妙,它用三种颜色来代表三种状态
- WHITE代表未访问的结点
- GRAY代表该节点第一次被访问
- BLACK代表该节点的所有邻接节点都被访问,即回溯完毕的第二次访问
以下是一个深度优先遍历的递归实现:
DFS(G, s)
for 在图G中的每一个节点v
status[v] = WHITE
// 进行其他初始
DFS-VISIT(s)
DFS-VISIT(v)
status[v] = GRAY
for 每一个v的邻接节点
if (status[v] == WHITE)
DFS-VISIT(t)
status[v] = BLACK
如果想实现深度优先遍历的非递归实现,就需要用到stack来存储未被访问的节点,以便回溯时能够找到
DFS(G, s)
stack visted, unvisited
unvisited.push(s)
while (!unvisited.empty()) // 只有当unvisted不空
current = unvisited.pop()
for 每一个current的邻接节点v and 节点v不在visited中 // 在以上的图例中是按从右向左的方式来遍历这些邻接节点
unvisited.push(v)
visted.push(current)
非递归实现的图片实例,图片中显示了unvisted栈中的数据情况:
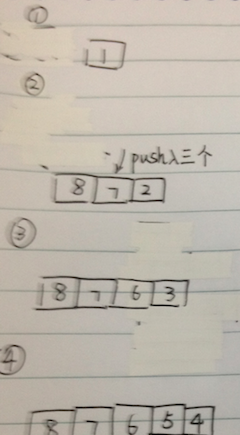
####深度优先搜索的伪码实现
深度优先搜索与深度优先遍历大部分实现是相同的,只是深度优先搜索会在找到终点时就退出搜索。
以下是深度优先搜索的伪码实现:
DFS(G, s, d)
stack visted, unvisited
unvisited.push(s)
while (!unvisited.empty()) // 只有当unvisted不空
current = unvisited.pop()
if (current == d)
break;
for 每一个current的邻接节点v and 节点不在visited中 // 在以上的图例中是按从右向左的方式来遍历这些邻接节点
v.prev = current
unvisited.push(v)
visted.push(current)
算法中通过记录每一个节点v都通过他的属性prev记录了他的前继节点是哪一个,最终可以通过前继节点构建出需要的路径。
####深度优先搜索的优化
谈到深度优先搜索的优化,我们可以想到在介绍中我们说过:DFS常常因为要搜索的图的某一条搜索路径太长(甚至是无限的)而陷入性能瓶颈,所以我们在优化时应当针对这一点进行优化,即限制每次搜索的路径长度,以便能够在一定长度的路径之内找到较优解,当在一定长度之内不能找到合适的路径时,我们可以增加限定的搜索路径长度,来进一步进行深度优先搜索,这种方法叫做逐层加深的深度优先算法。
我们根据上文中DFS的递归实现来对深度优先搜索,来对深度优先搜索做出优化。
DFS(G, s, d)
for 在图G中的每一个节点v
status[v] = WHITE
// 进行其他初始
for depth = 0
for max = 边数/2, 边数 do
if DFS-VISIT(s, d, depth, max)
break;
DFS-VISIT(v, d, depth, max)
if (depth > width)
return false
if (v == d)
return true
status[v] = GRAY
for 每一个v的邻接节点t
if (status[t] == WHITE)
t.prev = v
DFS-VISIT(t, d, depth + 1, max)
status[v] = BLACK
return false
####深度优先搜索的优点
深度优先搜索,与广度优先搜索相比,它不必遍历所有分支,所以它的速度较快。它不一定能找到最优解,但能找到接近解。
####深度优先搜索的应用
-
深度优先的第一种应用:走迷宫,上一章列出的代码是寻找一条有效的路径,深度优先也可以穷举出迷宫中所有的路径。只需要在每次找到迷宫出口时,不要结束程序,而继续回溯,就可以继续寻找其他走出迷宫的办法,直到变量step为0,程序退出。你可以记录每一种走法的路径长度(step),最后得到最优解。
-
深度优先的第二种应用:穷举。用例子说明:列出 A ~ F 这六个字母所能列出的所有组合(必须6位,不允许重复)。当然你可以用6重循环给出答案,但是随着字母数量增多,深度优先会是你的不二选择。下面继续通过一些例子说明应用吧,著名的“八皇后问题”,“背包问题”(当然也都可以用其他算法),大家可以在百度上搜索这两个东东。
来源:oschina
链接:https://my.oschina.net/u/729553/blog/184302