简介

jump consistent hash是一种一致性哈希算法, 此算法零内存消耗，均匀分配，快速，并且只有5行代码。

此算法适合使用在分shard的分布式存储系统中。

此算法的作者是 Google 的 John Lamping 和 Eric Veach，论文原文在 http://arxiv.org/ftp/arxiv/papers/1406/1406.2294.pdf

完整代码：

    
    int32_t JumpConsistentHash(uint64_t key, int32_t num_buckets) {
        int64_t b = -1, j = 0;
        while (j < num_buckets) {
            b = j;
            key = key * 2862933555777941757ULL + 1;
            j = (b + 1) * (double(1LL << 31) / double((key >> 33) + 1));
        }
        return b;
    }

输入是一个64位的key，和桶的数量（一般对应服务器的数量），输出是一个桶的编号。

原理解释：

下面byron根据论文的推导过程，做个翻译：

jump consistent hash的设计目标是：

平衡性，把对象均匀地分布在所有桶中。
单调性，当桶的数量变化时，只需要把一些对象从旧桶移动到新桶，不需要做其它移动。

jump consistent hash的设计思路是：计算当bucket数量变化时，有哪些输出需要变化。

让我们循序渐进地思考：

记 ch(key,num_buckets) 为num_buckets时的hash函数。
当num_buckets=1时，由于只有1个桶，显而易见，对任意k，有ch(k,1)==0。
当num_buckets=2时，为了使hash的结果保持均匀，ch(k,2)的结果应该有占比1/2的结果保持为0，有1/2跳变为1。
由此，一般规律是：num_buckets从n变化到n+1后，ch(k,n+1) 的结果中，应该有占比 n/(n+1) 的结果保持不变，而有 1/(n+1) 跳变为 n+1。

因此，我们可以用一个随机数生成器，来决定每次要不要跳变，并且让这个随机数生成器的状态仅仅依赖于key。就得到下面这个初步代码：

    int ch(int key, int num_buckets) {
        random.seed(key) ;
        int b = 0; // This will track ch(key, j +1) .
        for (int j = 1; j < num_buckets; j ++) {
            if (random.next() < 1.0/(j+1) ) b = j ;
        }  
        return b;
    }

显而易见，这个算法是O(n)的。同时我们可以发现，大多数情况下b=j 是不会执行的，而且随着 j 越来越大，这个概率越来越低。
那么有没有办法根据一个随机数，直接得出下一个跳变的 j ，降低时间复杂度呢？

ok,请把你的大脑切换到概率论模式。

我们可以把 ch(key,bum_buckets) 看做一个随机变量，

上述算法，追踪了桶编号的的跳变过程，我们记上一个跳变结果是b，假设下一个结果以一定概率是 j ，那么从b+1到j-1，这中间的多次增加桶都不能跳变。对于在区间 (b, j) 内的任意整数 i ，j是下一个结果的概率可以记为:

P( j>=i ) = P( ch(k,i)==ch(k,b+1) )

其中 ch(k,i)==ch(k,b+1) 意即从b+1到i的过程中，连续多次增加桶的时候都没有跳变，这个概率也就是连续多次不跳变事件概率的乘积，因此：

P(j>=i) = P( ch(k,b+1)==ch(k,b+2)) * P( ch(k,b+2)==ch(k,b+3)) * P( ch(k,b+3)==ch(k,b+4)) * ...... * P( ch(k,i-1)==ch(k,i))

由于单次不跳变的概率：

P( ch(k,i)==ch(k,i+1) ) = i/(i+1)

所以连续多次不跳变的概率

P(j>=i) = (b+1)/(b+2) * (b+2)/(b+3) * ... * (i-1)/i

前后项分子分母相互抵消，得到：

P(j>=i) = (b+1)/i

意即：j>=i的概率为(b+1)/i

此时，我们取一个在[0,1]区间均匀分布的随机数r，规定 r<(b+1)/i，就有j>=i，
所以有 i<(b+1)/r，这样就得到了i的上界是 (b+1)/r，由于对任意的i都要有j>=i，所以
j=floor( (b+1)/r )，这样我们用一个随机数r得到了j。

因此，代码可以改进为：

    int ch(int key, int num_buckets) {
        random. seed(key) ;
        int b = -1; //  bucket number before the previous jump
        int j = 0; // bucket number before the current jump
        while(j<num_buckets){
            b=j;
            double r=random.next(); //  0<r<1.0
            j = floor( (b+1) /r);
        }
        return b;
    }

这个算法的时间复杂度，可以假设每次r都取0.5，则可以认为每次 j=2*j，因此时间复杂度为O(log(n))。

此处需要一个均匀的伪随机数生成器，论文中使用了一个64位的线性同余随机数生成器。

需要指出的是：不像割环法，jump consistent hash不需要对key做hash，这是由于jump consistent hash使用内置的伪随机数生成器，来对每一次key做再hash，（byron的理解：所以结果分布的均匀性与输入key的分布无关，由伪随机数生成器的均匀性保证）。

各项指标对比分析：

consistent hash的概念出自David Karger的论文，经典并且应用广泛的割环法即出自这篇论文：http://www.ra.ethz.ch/cdstore/www8/data/2181/pdf/pd1.pdf

Karger提出2种实现:

"version A"，用 std::map<uint64_t, int32_t>表示key的hash 到桶id的映射。
"version B"，用 vector<pair<uint64_t, int32_t> >存储，vector事先排好序，用二分查找。

这两种实现的查找时间复杂度也都是O(log(n))

jump consistent hash的论文中，用jump consistent hash和Karger的割环算法做了对比，结果如下：

1. key分布的均匀性

直接从论文中摘录如下表格：

{% img /images/blog/jmp_consistent_hash_distribution.png %}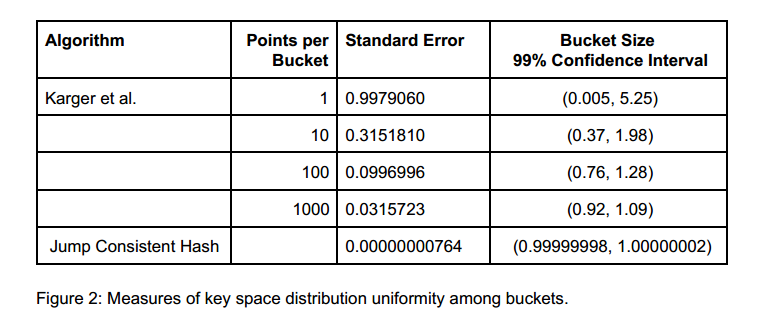

从标准差(Standard Error)这一列可见，jump consistent hash的均匀性要胜过割环法。

并且显而易见，jump consistent hash，当扩/缩容时，跳变key数量已经是理论最少值 1/n。

2. 执行耗时

下面是论文中的执行耗时对比图，其中k=1000。

{% img /images/blog/jmp_consistent_hash_cpu.png %}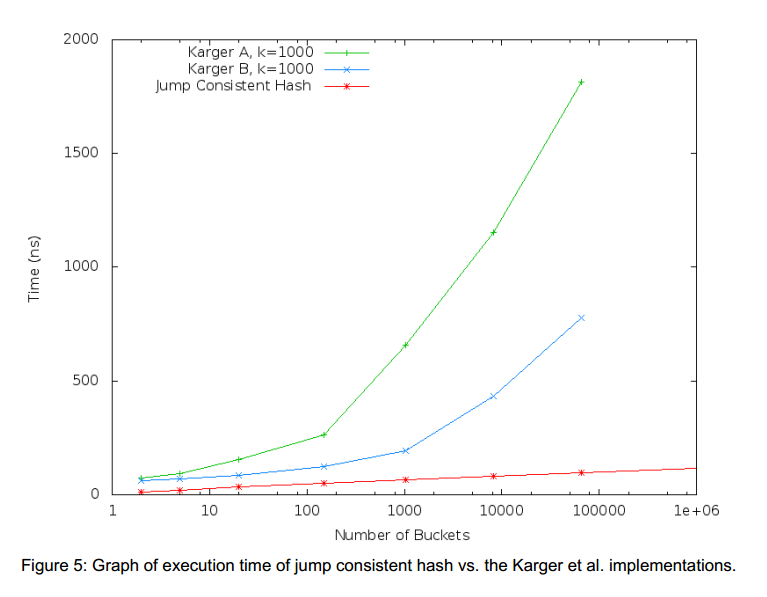

3. 内存占用对比

显而易见，请自行脑补

4. 初始化耗时对比