一、进制转换
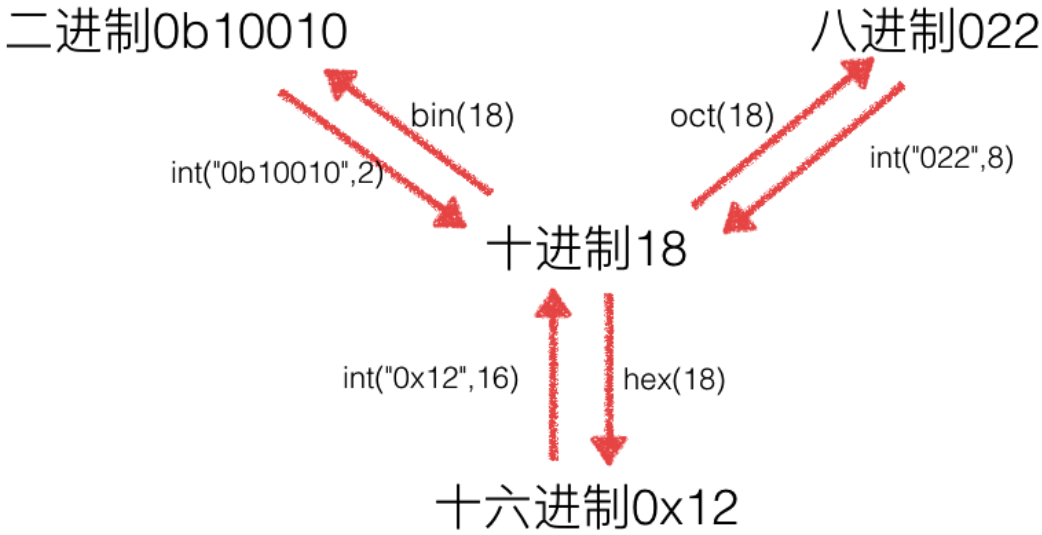
编程用十进制,十进制转换为二进制、八进制、十六进制
In [135]: bin(23) Out[135]: '0b10111' In [136]: oct(23) Out[136]: '0o27' In [137]: hex(23) Out[137]: '0x17'
也可以直接反向获取十进制
In [146]: 0b10111 Out[146]: 23 In [147]: 0o27 Out[147]: 23 In [148]: 0x17 Out[148]: 23
也可以用int函数来转换
In [149]: int('0b10111', 2)
Out[149]: 23
In [150]: int('0o27', 8)
Out[150]: 23
In [151]: int('0x17', 16)
Out[151]: 23
二、位运算
按位异或的3个特点:
(1) 0^0=0,0^1=1 0异或任何数=任何数
(2) 1^0=1,1^1=0 1异或任何数-任何数取反
(3) 任何数异或自己=把自己置0
按位异或的几个常见用途:
(1) 使某些特定的位翻转
例如对数10100001的第2位和第3位翻转,则可以将该数与00000110进行按位异或运算。
10100001^00000110 = 10100111
(2) 实现两个值的交换,而不必使用临时变量
例如交换两个整数a=10100001,b=00000110的值,可通过下列语句实现:
a = a^b; //a=10100111
b = b^a; //b=10100001
a = a^b; //a=00000110
- & 按位与
- | 按位或
- ^ 按位异或
- ~ 按位取反
- << 按位左移
- >> 按位右移
- 用途: 直接操作二进制,省内存,效率高
1)<<按位左移
各二进位全部左移n位,高位丢弃,低位补0
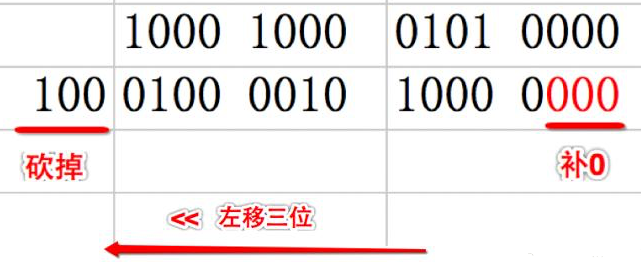
x << n 左移 x 的所有二进制位向左移动n位,移出位删掉,移进的位补零
【注意事项】
- a. 左移1位相当于乘以2
- 用途:快速计算一个数乘以2的n次方 (8<<3 等同于8*2^3)
- b.左移可能会改变一个数的正负性
2)>>右移
各二进位全部右移n位,保持符号位不变
x >> n, x的所有二进制位向右移动n位,移出的位删掉,移进的位补符号位, 右移不会改变一个数的符号
【注意事项】
- 右移1位相当于除以2
- x 右移 n 位就相当于除以2的n次方
- 用途: 快速计算一个数除以2的n次方 (8>>3 等同于8/2^3)

3)& 按位与
全1才1否则0 :只有对应的两个二进位均为1时,结果位才为1,否则为0
4) | 按位或
有1就1 只要对应的二个二进位有一个为1时,结果位就为1,否则为0
5) ^ 按位异或
不同为1 当对应的二进位相异(不相同)时,结果为1,否则为0
6) ~ 取反
~9 = -10
【为什么9取反变成了-10的说明】:
9的原码 ==> 0000 1001 因为正数的原码=反码=补码,所以在 真正存储的时候就是0000 1001
接下来进行对9的补码进行取反操作
进行取反==> 1111 0110 这就是对9 进行了取反之后的补码
既然已经知道了补码,那么接下来只要转换为 咱们人能识别的码型就可以,因此按照规则 ,把这个1111 0110 这个补码 转换为原码即可
符号位不变,其它位取反==> 1000 1001
三、例题
1. 输入一个正数,输出该数二进制表示中1的个数
知识点:把一个整数减去1,再和原整数做与运算,会把该整数最右边一个1变成0。那么一个整数的二进制表示中有多少个1,就可以进行多少次这样的操作。
总结:把一个整数减去1之后再和原来的整数做位与运算,得到的结果相当于是把整数的二进制表示中的最右边一个1变成0 。
代码如下:
def count(n):
num = 0
while n:
n &= (n-1)
num += 1
return num
2. 输入两个整数m和n,计算需要改变m的二进制表示中的多少位才能得到n
解决方法:第一步,求这两个数的与或;第二步,统计异或结果中1的位数。
代码如下:
def mton(m,n):
yihuo = m^n
count = 0
while yihuo:
yihuo &= (yihuo-1)
count += 1
print(count)
3. 用一条语句判断一个整数是不是2的整数次方
解决方法:一个整数如果是2的整数次方,那么它的二进制表示中有且只有一位是1,而其它所有位都是0 。根据前面的分析,把这个整数减去1后再和它自己做与运算,这个整数中唯一的1就变成0了。
代码如下:
def judgebinary(x):
if x&(x-1) == 0:
return True
return False
4.不使用运算符 + 和 - ,计算两整数 a 、b 之和
示例:
示例 1: 输入: a = 1, b = 2 输出: 3 示例 2: 输入: a = -2, b = 3 输出: 1
代码如下:
def getSum(a, b):
"""
:type a: int
:type b: int
:rtype: int
"""
#位操作
no_carry_sum=a^b #a与b不进位时的和,恰好与异或性质一样
print(no_carry_sum)
carry=(a&b)<<1 #a与b的和的进位,恰好是与或操作再左移一位
print(carry)
return sum([no_carry_sum,carry])#前两者之和
res = getSum(12,3)
print(res)
总结:两个数的和可以通过将这两个数异或得到这个数不进位时的和,再将这两个数进行与或再左移一位,相当于进位的操作,再将这两个数相加,就可以得到两个数的和
5.判断数字n的二进制数从右往左数第i位是否为1
思路:1<<i可以表示从右向左第i位为1,其余位为0的指示数,
用n与有特定位的指示数与或,就能判断n的特定位是否为1,【长数和短数与或只比较到短数的长度】
举例:10的二进制数倒数第2位是否为1, 10--1010, 1<<1=2--10, 1010&10 = True
代码如下:
def isOne(n,i):
print(n,1<<i)
return (n&(1<<i))!=0
res = isOne(10,1)
print(res) #True
参考文献:
【2】深入理解按位异或运算符
来源:https://www.cnblogs.com/nxf-rabbit75/p/10291792.html