一、红黑树介绍
红黑树是特殊的二叉查找树,具有以下五个特点:
(1) 节点为黑色或红色
(2)根节点为黑色
(3) 红色节点不能连续
(4)根节点到NIL节点的各个路径上黑色节点数量相同
(5)NIL节点为黑色,NIL节点为叶节点的空的孩子
根据性质(4)可知,红色节点具有0或2个孩子。
二、左旋和右旋
在红黑树删除和插入之后,为了保持红黑树的状态,可能需要用到左旋和右旋两种操作,左旋和右旋操作不改变红黑树是二叉查找树的特点。
(1)左旋
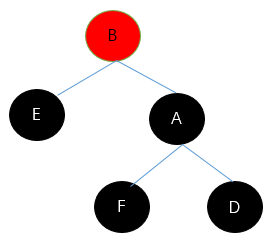
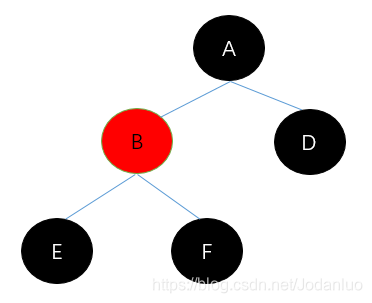
(2)右旋


三、插入算法思想
红黑树在插入新节点时可能会改变红黑树的性质,在新节点插入时,需要根据以下几种情况做相应的操作,新节点插入默认为红色(对红黑树平衡影响最小),插入的节点都会成为叶节点。假设插入节点(当前节点)为Q,父节点为P,叔父节点为B,祖父节点为G,插入新节点时会遇到一下几种情况,可根据不同的情况做不同的操作。
| P | B | G | |
| (1) | 黑 | 红/黑 | 黑/红 |
| (2) | 红 | 红 | 黑 |
| (3) | 红 | 黑 | 黑 |
(1)直接插入新节点
(2)插入Q后,将P和B变成黑色,G变为红色,再将G视为Q,进行下一轮的判断,进入平衡调节阶段。
(3)a、若Q为P的左子,P为G的左子,则调换P和G 的颜色,并对P进行右旋,完成调节
b、若Q为P的右子,P为G的左子,先对P进行左旋,转化为情况a。
c、若Q为P的右子,P为G的右子,则调换P和G的颜色,并对P进行左旋,完成调节。
d、若Q为P的左子,P为G的右子,先对P进行右旋,转换为情况c。
此外若Q为根节点,直接将Q置为黑色即可,情况(3)是平衡调节阶段会遇到的情况。
四、删除算法思想
删除操作给红黑树带来的影响比较大,因为删除节点可能是叶节点或是非叶节点,当要删除一个节点时,可能会遇到以下几种情况:
(1)删除的节点无孩子,若节点为红色,则直接删除(不影响红黑树性质),若节点为黑色,先再进行平衡调节再删除。
(2)删除的节点只有一个孩子,由红黑树的性质可得,该节点为黑色,且孩子为红色,则将该节点和孩子节点进行数值调换,转换为情况(1)
(3)删除的节点有两个孩子,则将该节点和右子树中最小的节点进行数值调换,转换为情况(2)或情况(1)
总结三种情况,在进行删除操作时,首先要做的就是将节点位置调换到叶节点位置,然后再进行平衡调节。平衡调节的步骤如下:Q为当前节点,B为兄弟节点,P为父节点,BN为近侄子节点,BF为远侄子节点
| Q | B | P | BN | BF | |
| (1) | 黑 | 红 | 黑 | 黑 | 黑 |
| (2) | 黑 | 黑 | 红 | 黑 | 黑 |
| (3) | 黑 | 黑 | 黑 | 黑 | 黑 |
| (4) | 黑 | 黑 | 红/黑 | 黑/红 | 红 |
| (5) | 黑 | 黑 | 红/黑 | 红 | 黑 |
(1)将B和P进行颜色调换,然后将P向Q的方向进行左旋或者右旋,转换为情况(2),Q不变
(2)将B置为红色,P置为黑色,完成平衡调节
(3)将B置为红色,P视为Q,进行下一轮判断,最终可能转换为(2)或者一直N取到根节点,取到根节点时结束
(4)将P和BF置为黑色,B置为P的颜色,然后将P向Q的方向进行左旋或者右旋,完成平衡调节
(5)将WN与B进行颜色调换,并将B向BF方向进行左旋或者右旋,转换为情况(4),Q不变
来源:CSDN
作者:Jodanluo
链接:https://blog.csdn.net/Jodanluo/article/details/104180400