普里姆算法(Prim)和克鲁斯卡尔(Kruskal)算法

普里姆算法(Prim)和克鲁斯卡尔(Kruskal)算法  

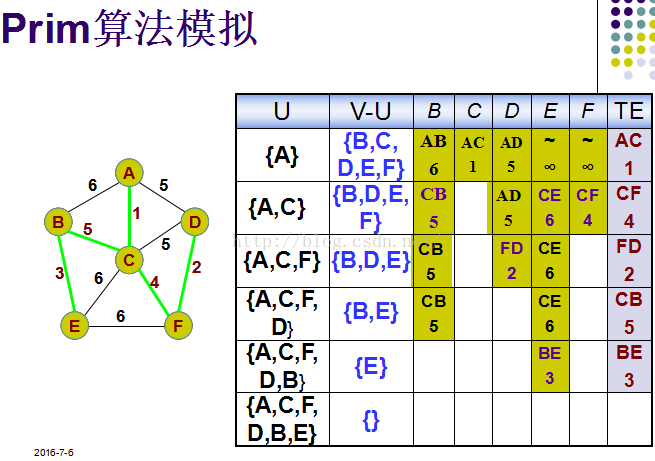
普里姆算法的基本思想:

取图中任意一个顶点 v 作为生成树的根，之后往生成树上添加新的顶点 w。添加顶点w的条件为：w 和已在生成树上的顶点v 之间必定存在一条边，并且该边的权值在所有连通顶点 v 和 w 之间的边中取值最小。之后继续往生成树上添加顶点，直至生成树上含有 n-1 个顶点为止。

最小生成树的构建：

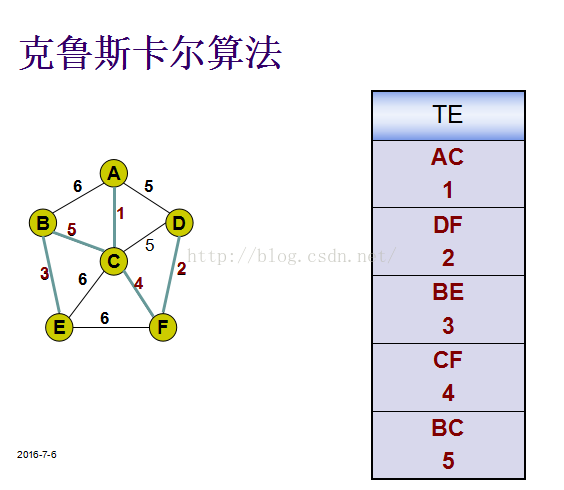
克鲁斯卡尔算法的基本思想：

考虑问题的出发点: 为使生成树上边的权值之和达到最小，则应使生成树中每一条边的权值尽可能地小。

 

具体做法: 先构造一个只含 n 个顶点的子图 SG，然后从权值最小的边开始，若它的添加不使SG 中产生回路，则在 SG 上加上这条边，如此重复，直至加上 n-1 条边为止。

最小生成树的构建：

 

来源：CSDN

作者：zhupengqq1

链接：https://blog.csdn.net/zhupengqq1/article/details/104141689