C++排序算法之快速排序

思路

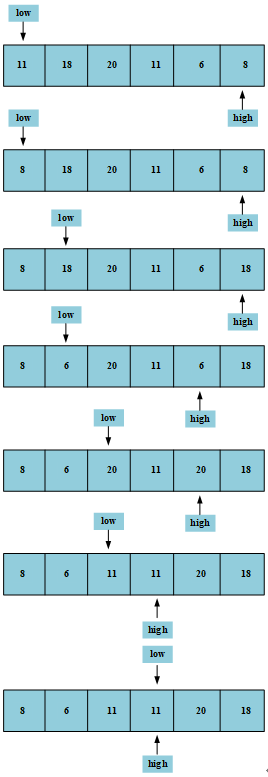
如下图所示，对于数组s={11，18，20，11，6，8}，选择11作为关键字key，然后选择两个哨兵low和high分别从数组的首部和尾部出发，执行以下操作：

1. 循环判断尾部哨兵所在元素是否大于key，且low<high，若是则哨兵high–，循环继续；否则循环停止，执行s[low]=s[high]，然后转到2。
2. 循环判断首部哨兵所在元素是否小于或等于key，且low<high，若是则哨兵low++，循环继续；否则循环停止，执行s[high]=s[low]，然后转到3。
3. 若low>=high，循环停止，否则转到1。

C++实现

int partion(vector<int>& s, int low, int high) {
	int key = s[low];
	while(low < high) {
		while(low < high && s[high] > key)
			high--; 
		s[low] = s[high];
		while(low < high && s[low] <= key)
			low++;
		s[high] = s[low];
	}
	s[low] = key;
	return low;
}

void quickSort(vector<int>& s, int low, int high) {
	if(low >= high) return;
	int index = partion(s, low, high);
	quickSort(s, low, index - 1);
	quickSort(s, index + 1, high);
}

总结

• 最优的情况就是每次取到的元素都刚好平分整个数组，即T[n]=2T[n/2]+f(n).此时最优复杂度为O(nlogn).
• 最差情况下时间复杂度就是每一次取到的元素都是数组中最小或最大的，这种情况等价于冒泡排序，即T[n]=n(n-1).此时最差情况下时间复杂度为O(n^2);
• 平均时间复杂度为O(nlogn).
• 首先就地快速排序使用的空间是O(1);而真正消耗空间的就是递归调用，因为每次递归要保存一些数据;最优情况下空间复杂度为O(logn);最差情况下空间复杂度为O(n).

来源：CSDN

作者：Black.Spider

链接：https://blog.csdn.net/weixin_43519984/article/details/104086967