本系列博客作为记录花书的一些知识点,一些“显而易见”的,我就不多写了
2.1 标量、向量、矩阵和张量
标量:一个单独的数。
向量:一列数。
矩阵:一个二维数组。
张量:一个数组中的元素分布在若干维坐标的规则网络中,我们称之为张量。
转置:矩阵的转置是以对角线为轴的镜像。
2.2 矩阵和向量相乘
矩阵乘积:
元素对应乘积(Hadamard乘积):两个矩阵的标准乘积不是指两个矩阵中对应元素的乘积。不过,那样的矩阵操作确实是存在的,被称为元素对应乘积(element-wise product)或者Hadamard 乘积(Hadamard product),记为 A ⊙ B。
点积:两个相同维数的向量 x 和 y 的点积(dot product)可看作是矩阵乘积 x ⊤ y。
2.3 单位矩阵和逆矩阵
单位矩阵: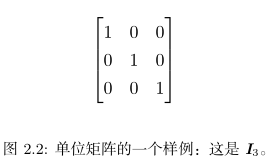
逆矩阵: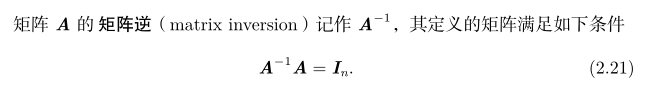
2.4 线性相关和生成子空间
线性相关:
线性无关:如果一组向量中的任意一个向量都不能表示成其他向量的线性组合,那么这组向量称为线性无关。
2.5 范数
1.
2.范数是满足下列性质的任意函数:
3.p=2时,L²范数是欧几里得范数,表示从原点出发到向量x确定的点的欧几里得距离。
4.平方L²范数也经常用来衡量向量的大小,可以简单的通过点积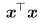 计算。
计算。
5.平方L²范数在计算上比L²范数本身方便,但是它在原点附近增长得十分缓慢。在某些机器学习应用中,区分恰好是零的元素和非零但值很小的元素是很重要的。
6.L¹范数: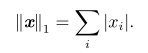
7.Lº范数(这个术语只是一些坐着自己叫的):统计向量中非零元素的个数来衡量向量的大小。
8.最大范数:
9.Frobenius范数:
10.两个向量的点积
2.6 特殊类型的矩阵和向量
1.对角矩阵
2.对称矩阵
3.单位向量
4.标准正交
5.正交矩阵
2.7 特征分解
1.
2.所有特征值都是正数的矩阵被称为正定(positive definite);所有特征值都是非负数的矩阵被称为半正定(positive semidefinite)。同样地,所有特征值都是负数的矩阵被称为负定(negative definite);所有特征值都是非正数的矩阵被称为半负定(negative semidefinite)。半正定矩阵受到关注是因为它们保证 ∀x,x ⊤ Ax ≥ 0。此外,正定矩阵还保证 x ⊤ Ax = 0 ⇒ x = 0。
2.8 奇异值分解
1.
2.对角矩阵 D 对角线上的元素被称为矩阵 A 的奇异值(singular value)。矩阵U 的列向量被称为左奇异向量(left singular vector),矩阵 V 的列向量被称右奇异向量(right singular vector)。
2.9 Moore-Penrose伪逆

2.10 迹运算
1.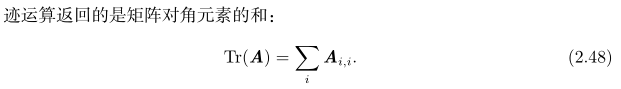
2.
3.
4.
5.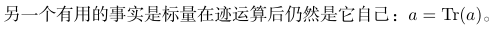
2.11 行列式
行列式,记作 det(A),是一个将方阵 A 映射到实数的函数。行列式等于矩阵特征值的乘积。行列式的绝对值可以用来衡量矩阵参与矩阵乘法后空间扩大或者缩小了多少。如果行列式是 0,那么空间至少沿着某一维完全收缩了,使其失去了所有的体积。如果行列式是 1,那么这个转换保持空间体积不变。
2.12 主成分分析(PCA)
来源:CSDN
作者:XY丶YX
链接:https://blog.csdn.net/qq_37792173/article/details/103944155