1. 技术文章
  2. 快速傅里叶变换fft

快速傅里叶变换fft

由 对着背影说爱祢 提交于 2020-01-10 19:12:31

1.傅里叶变换

傅里叶变换是一个很重要的变换方法。大部分人对傅里叶变换的理解就是，它实现了信号从时域到频域的转换，而从数学的角度来看，傅里叶变换其实就是一种基底变换（通俗地说就是改变原来的坐标系）。然而，不论从什么角度来理解傅里叶变换，我们只要记住，它的本质就是一个序列\(f\)到另一个序列的\(F\)转换（连续或离散）。
傅里叶变换的研究和应用都非常多，因此本文不再赘述相关的内容，如果想通俗且深入地理解傅里叶变换，我推荐马同学的博客。
一般的傅里叶变换通常指以下的公式：
\[F(j\omega)=\int_{-\infty}^{\infty}f(t)e^{-j\omega t}dt\]
为了和离散傅里叶变换区别，我们称其为连续傅里叶变换。

2.离散傅里叶变换DFT

由前文可知，连续傅里叶变换的公式如下：
\[F(j\omega)=\int_{-\infty}^{\infty}f(t)e^{-j\omega t}dt\]
现实中，我们一般无法得到连续的观察序列\(f(t)\)，只能通过采样的方式得到离散的子序列\(f[k]\)。比较严谨的定义是：从连续的时间序列\(f(t)\)中按给定周期\(T\)采样\(N\)个点，\(f[0],f[1],\dots,f[N-1]\)，这\(N\)个点组成了\(f(t)\)的一个离散子序列\(f[k]\)。
我们用离散序列\(f[k]\)来估计\(f(t)\)的傅里叶变换结果\(F(j\omega)\)，基于dft的公式，很容易可以得到：
\[\begin{aligned} F(j\omega)&=\int_{0}^{(N-1)T}f(t)e^{-j\omega t}dt\\ &=f[0]e^{-j0}+f[1]e^{-j\omega T}+\dots+f[k]e^{-j\omega kT}+\dots+f[N-1]e^{-j\omega(N-1)T}\\ &=\sum_{k=0}^{N-1}f[k]e^{-j\omega kT} \end{aligned}\]
因此，我们得到了基于离散子序列\(f[k]\)的变换公式：
\[F(j\omega)=\sum_{k=0}^{N-1}f[k]e^{-j\omega kT}\]
实际上，我们也无法得到真正的\(F(j\omega)\)（连续的），只能用插值的方式做估计（离散的），类似于从\(f(t)\)中采样得到\(f[k]\)，我们也可以取\(F(j\omega)\)的\(N\)个离散值来做估计。由于\(f[k]\)是以\(T\)为周期采样的，所以\(\omega\)的插值范围应该落在区间\([0, \frac{2\pi}{T})上\)（假设有\(\frac{2\pi}{T_{1}}>\frac{2\pi}{T}\)，则\(T_{1}< T\)，比我们采样的周期小）。在区间\([0, \frac{2\pi}{T})\)中均匀取\(N\)个点，可以得到\(\omega\)的\(N\)个插值点：
\[\omega=0,\frac{2\pi}{NT},\frac{2\pi}{NT}\times 2,\dots,\frac{2\pi}{NT}\times n,\dots,\frac{2\pi}{NT}\times(N-1)\]
把\(\omega\)代入上面的公式，可以得到离散傅里叶变换（dft）公式：
\[F[n]=\sum_{k=0}^{N-1}f[k]e^{-j\frac{2\pi}{N}nk},(n=0,1,\dots,N-1)\]
我们将离散傅里叶变换简称为dft，为了方便起见，后面统一用dft表示离散傅里叶变换。
根据上面的公式，可以很容易计算出任何离散序列的dft，对应的代码（python）如下：

import cmath
import numpy as np

def dft(ts):
    """ discrete fourier transformer
    """
    N = len(ts)
    F = np.zeros(N, dtype=np.complex)
    for n in range(N):
        for k, f in enumerate(ts):
            F[n] += f * cmath.exp(-2j*cmath.pi/N*(n*k))
    return F

从代码中可以看到，计算dft需要做嵌套的\(N\)次遍历，因此使用这种方式计算dft的时间复杂度是\(O(n^{2})\)，当\(n\)值很大时（比如\(n=1000\)），dft的计算会相当耗时，所以现实中一般使用快速傅里叶变换（fft）来计算dft。

3.快速傅里叶变换FFT和逆变换IFFT

快速傅里叶变换（fft）是一种优化的dft计算方法，核心思想是分治，为了方便，后面统一用fft指代快速傅里叶变换算法。在讲解fft之前，先复习一下dft的公式，
\[F[n]=\sum_{k=0}^{N-1}f[k]e^{-j\frac{2\pi}{N}nk},(n=0,1,\dots,N-1)\]
公式中的变量\(e^{-j\frac{2\pi}{N}nk}\)看起来有些复杂，我们可以用简单的变量来代替，所以令
\[W_{N}^{nk}=e^{-j\frac{2\pi}{N}nk}\]
则原dft公式可以重写成：
\[F[n]=\sum_{k=0}^{N-1}f[k]W_{N}^{nk},(n=0,1,\dots,N-1)\]
变量\(W_{N}^{nk}\)有以下几个性质：

  1. \(W_{N}^{mN}=1,m=0,1,2,\dots\)
  2. 当N是偶数时，\(W_{N}^{mN+N/2}=-1,m=0,1,2,\dots\)
  3. \(W_{N}^{d+mN}=W_{N}^{d},d=0,1,N-1\)
  4. 当N是偶数时，\(W_{N}^{d+mN+N/2}=-W_{N}^{d},d=0,1,\frac{N}{2}-1\)

这几个性质的证明都很简单，对于性质1，我们有
\[W_{N}^{mN}=e^{-j\frac{2\pi}{N}mN}=e^{-j2m\pi}=1\]
对于性质2，我们有
\[W_{N}^{mN+N/2}=W_{N}^{N/2}=e^{-j\frac{2\pi}{N}\frac{N}{2}}=e^{-j\pi}=-1\]
对于性质3，我们有
\[W_{N}^{d+mN}=W_{N}^{mN}W_{N}^{d}=W_{N}^{d}\]
对于性质4，我们有
\[W_{N}^{d+mN+N/2}=W_{N}^{d}W_{N}^{mN}W_{N}^{N/2}=-W_{N}^{d}\]
这几个性质正是后面我们推导fft时所要用到的。

3.1.快速傅里叶变换FFT

假设\(N\)是2的幂，即\(N=2^{l}, l=1,2,3,\dots\)。我们对\(\sum_{k=0}^{N-1}f[k]W_{N}^{nk}\)中的项按\(k\)的奇偶分组，可以得到：
\[\begin{aligned} F[n]&=\sum_{k=0}^{N-1}f[k]W_{N}^{nk},(n=0,1,\dots,N-1)\\ &=\sum_{k=0}^{\frac{N}{2}-1}f[2k]W_{N}^{2nk}+W_{N}^{n}\sum_{k=0}^{\frac{N}{2}-1}f[2k+1]W_{N}^{2nk}\\ &=\sum_{k=0}^{\frac{N}{2}-1}f[2k]W_{N/2}^{nk}+W_{N}^{n}\sum_{k=0}^{\frac{N}{2}-1}f[2k+1]W_{N/2}^{nk} \end{aligned}\]
当\(n\geq\frac{N}{2}\)时，不妨令\(n=n_{1}+\frac{N}{2}， n_{1}=0,1,2,\dots,\frac{N}{2}-1\)，则有：
\[\begin{aligned} F[n]&=\sum_{k=0}^{\frac{N}{2}-1}f[2k]W_{N/2}^{nk}+W_{N}^{n}\sum_{k=0}^{\frac{N}{2}-1}f[2k+1]W_{N/2}^{nk}\\ &=\sum_{k=0}^{\frac{N}{2}-1}f[2k]W_{N/2}^{n_{1}k+kN/2}+W_{N}^{n_{1}+N/2}\sum_{k=0}^{\frac{N}{2}-1}f[2k+1]W_{N/2}^{n_{1}k+kN/2}\\ &=\sum_{k=0}^{\frac{N}{2}-1}f[2k]W_{N/2}^{n_{1}k}-W_{N}^{n_{1}}\sum_{k=0}^{\frac{N}{2}-1}f[2k+1]W_{N/2}^{n_{1}k} \end{aligned}\]
进一步地，我们令
\[G[n]=\sum_{k=0}^{\frac{N}{2}-1}f[2k]W_{N/2}^{nk}, H[n]=\sum_{k=0}^{\frac{N}{2}-1}f[2k+1]W_{N/2}^{nk}\]
故当\(0\leq n<\frac{N}{2}\)时，有：
\[F[n]=G[n]+W_{N}^{n}H[n],F[n+N/2]=G[n]-W_{N}^{n}H[n]\]
举例来说，当\(N=8\)时，有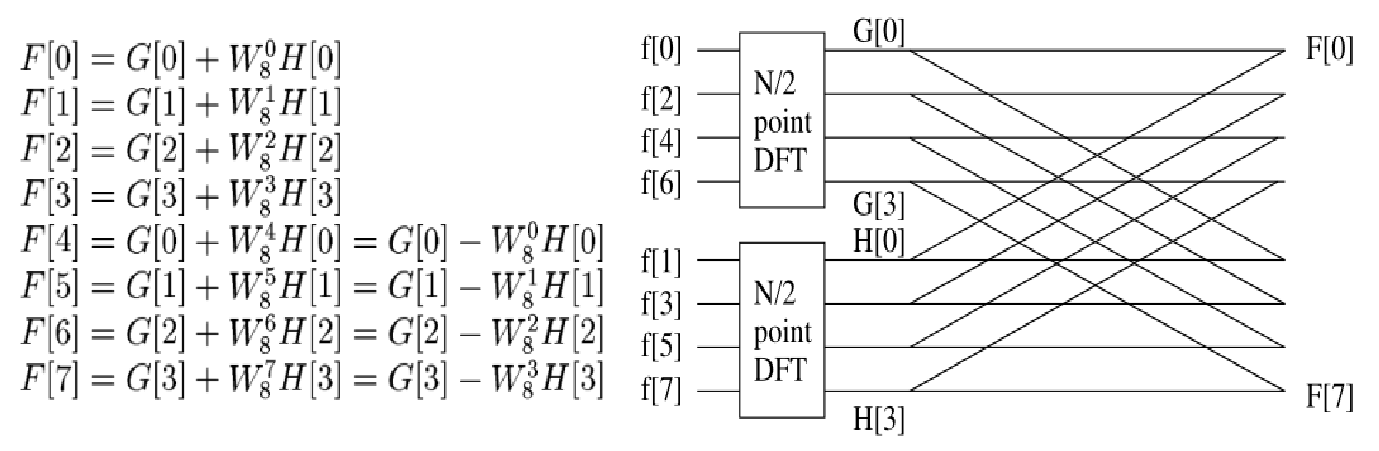
N=8

因为\(N\)是2的幂，所以\(G[n]\)和\(H[n]\)还可以像这样用奇偶分组的方式进一步拆解为更小粒度的分组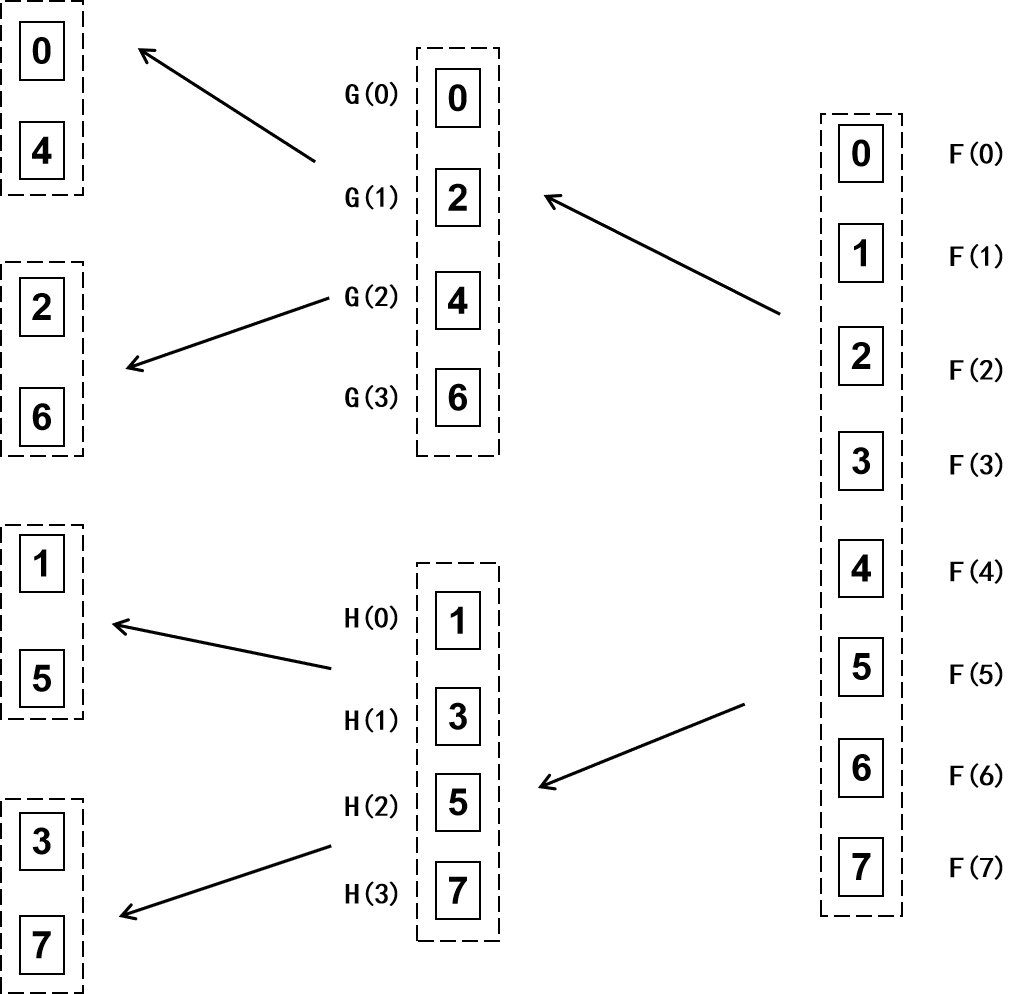
GH分组1

上述所有图里小方框内的数字表示的是原序列下标\(n\)，划分到最小粒度时，有\(N=2\)，即
\[G[n]=f(n), H[n]=f(n)\]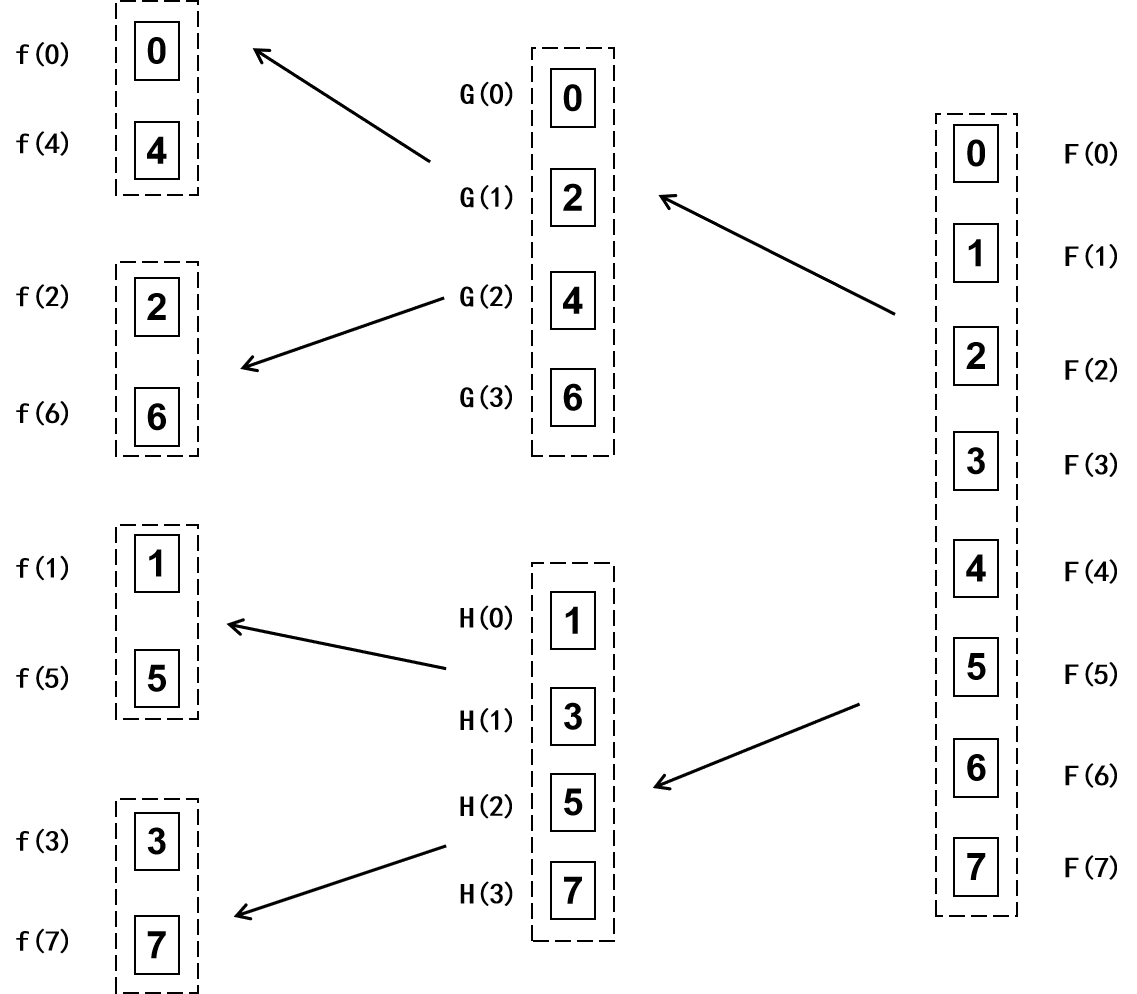
GH分组2

此时，\(G[n]\)项中的\(f[2k]W_{N/2}^{nk}\)里，\(k=0\)；\(H[n]\)项中的\(f[2k+1]W_{N/2}^{nk}\)里，\(k=0\)。

通过“蝴蝶变换”（buttferfly transform），我们可以依次从“小粒度的分组”不断合并得到“大粒度的分组”，下图中的四条红色线段和对应的点应组成了一个蝴蝶变换。
分组合并过程

更具体的蝴蝶变换如下图所示：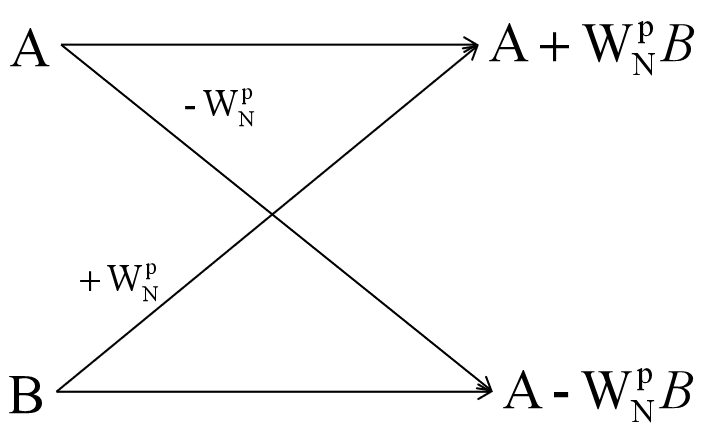
蝴蝶变换

观察每次分组中\(k\)值的变化，可以发现每次分组是按二进制位最后一位来判断的（0为偶，1为奇）
GH分组3

因此，我们在做分组的时候，可以使用递归的方式来做，每次递归时按二进制位的最后一位对序列分组，具体代码（python）如下：

import cmath
import numpy as np

def wnk(N, n):
    """ get W_N^n
    """
    return cmath.exp(-2j*n*cmath.pi/N)

def recursive_fft(f):
    """ recursive of fast fourier transform
    """
    N = len(f) # N is power of 2
    if N < 2:
        return f
    F = np.zeros(N, dtype=np.complex)
    G = recursive_fft([x for i,x in enumerate(f) if i%2 == 0]) # even 
    H = recursive_fft([x for i,x in enumerate(f) if i%2 == 1]) # odd
    for i, (g, h) in enumerate(zip(G, H)):
        # butterfly transform
        F[i] = g + wnk(N, i)*h
        F[i+N//2] = g - wnk(N, i)*h
    return F

使用递归的方法计算fft需要用到额外的变量G和H，而且递归有深度的限制，最好不使用递归便能达到我们迭代更新的目的。回顾我们之前的思路，是按“大粒度的分组”->“小粒度的分组”来进行更新的，如果能反过来，按“小粒度的分组”->“大粒度的分组”来更新，那么就不需要递归了。问题在于如何得到“小粒度的分组”？既然我们每次是根据\(k\)的最后一个二进制位来决定分组，那么如果我们将\(k\)的二制位倒置的话，不就可以得到按顺序排列的“小粒度分组”吗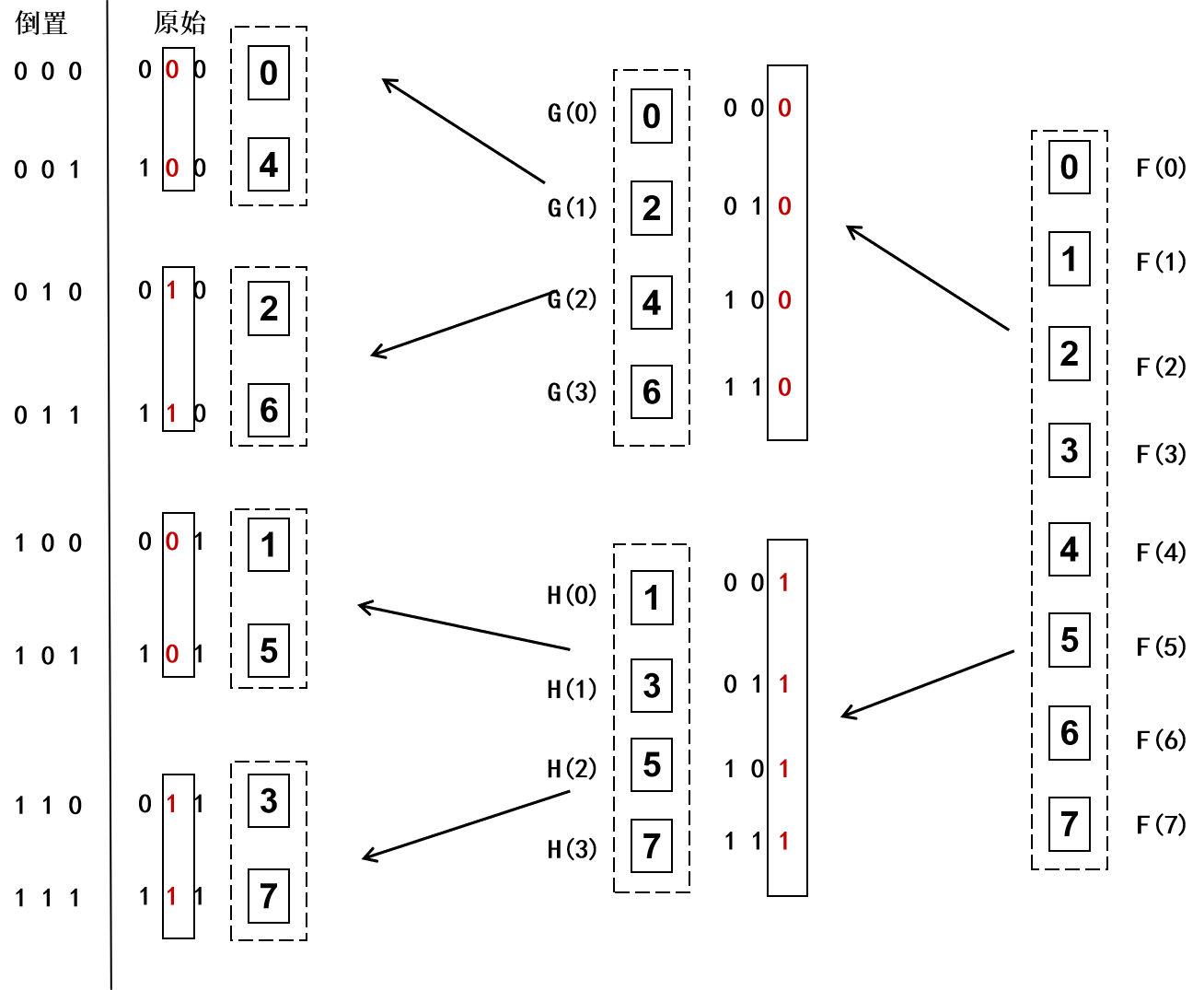
GH分组4

所以非递归的fft思路就很清晰了，

  1. 按\(k\)值的二进制反转调换原始序列
  2. 按\(step=2, 4, 8, \dots, \frac{N}{2}\)做迭代更新

非递归fft的代码（python）如下所示：

import cmath
import numpy as np

def wnk(N, n):
    """ get W_N^n
    """
    return cmath.exp(-2j*n*cmath.pi/N)

def get_bit(n):
    """ get highest bit of n
    """ 
    bit = 0
    while n != 0:
        n >>= 1
        bit += 1
    return bit

def flip_bits(bits, n):
    """ flip n bit of bits
    """
    assert n >= 0
    if n == 0:
        return bits
    y = 0
    while n > 0:
        y <<= 1
        y |= bits&1
        bits >>= 1
        n -= 1
    return y

def fft(f):
    """ fast discrete fourier transformer
    """
    N = len(f) # N is power of 2
    l = get_bit(N)
    # re-arange f by flipping bits
    F = np.zeros(N, dtype=np.complex)
    for i, a in enumerate(f):
        F[flip_bits(i, l-1)] = a
    
    step = 1
    while step < N:
        for i in range(0, N, 2*step):
            for j in range(i, i+step): 
                # butterfly transform
                a = F[j] + wnk(2*step, j)*F[j+step]
                b = F[j] - wnk(2*step, j)*F[j+step]
                F[j] = a
                F[j+step] = b 
        step *= 2
    
    return F

到这里，fft的计算逻辑已经基本最优了，但是，注意到每次分组内做蝴蝶变换时需要计算\(W_{N}^{n}\)，而实际上每次按序遍历\(G\)和\(H\)时，\(W_{N}^{n}\)是按\(W_{N}^{1}\)等比递增的，所以这里可以进一步优化来减少计算量。代码（python）如下所示：

import cmath
import numpy as np

WNK = [cmath.exp(-2j*cmath.pi/(1<<n)) for n in range(64)]

def get_bit(n):
    """ get highest bit of n
    """ 
    bit = 0
    while n != 0:
        n >>= 1
        bit += 1
    return bit

def flip_bits(bits, n):
    """ flip n bit of bits
    """
    assert n >= 0
    if n == 0:
        return bits
    y = 0
    while n > 0:
        y <<= 1
        y |= bits&1
        bits >>= 1
        n -= 1
    return y

def fft(f):
    """ fast discrete fourier transformer
    """
    N = len(f)
    l = get_bit(N)
    # re-arange ts by flipping bits
    F = np.zeros(N, dtype=np.complex)
    for i, a in enumerate(f):
        F[flip_bits(i, l-1)] = a
    
    step = 1
    cnt = 1
    while step < N:
        for i in range(0, N, 2*step):
            w = 1.0
            for j in range(i, i+step): 
                # butterfly transform
                a = F[j] + w*F[j+step]
                b = F[j] - w*F[j+step]
                w *= WNK[cnt]
                F[j] = a
                F[j+step] = b 
        step *= 2
        cnt += 1 
    
    return F

至此，fft的完整过程基本讲解完毕。

3.2.快速傅里叶逆变换IFFT

傅里叶逆变换（idft）的公式如下：
\[f[n]=\frac{1}{N}\sum_{k=0}^{N-1}F[k]e^{j\frac{2\pi}{N}nk},(n=0,1,\dots,N-1)\]
对比dft的公式可以发现二者基本一致，只不过\(W_{N}^{nk}=e^{j\frac{2\pi}{N}nk}\)，同时多了一个因子\(\frac{1}{N}\)。所以，只要在fft的过程中替换\(W_{N}^{nk}\)，并把最后的结果除以\(N\)就可以得到ifft。
最后，完整的fft和ifft代码（python）如下所示：

import cmath
import numpy as np

WNK = [cmath.exp(-2j*cmath.pi/(1<<n)) for n in range(64)]

def check_power2(n):
    """ check `n` is or not power of 2
    """
    return n > 0 and n&(n-1) == 0

def get_bit(n):
    """ get highest bit of n
    """ 
    bit = 0
    while n != 0:
        n >>= 1
        bit += 1
    return bit

def flip_bits(bits, n):
    """ flip n bit of bits
    """
    assert n >= 0
    if n == 0:
        return bits
    y = 0
    while n > 0:
        y <<= 1
        y |= bits&1
        bits >>= 1
        n -= 1
    return y

def fft(ts):
    """ fast fourier transformer
    """
    return fdft(ts)

def ifft(ts):
    """ reverse fast fourier transformer 
    """
    return fdft(ts, reverse=True)

def fdft(f, reverse=False):
    """ fast discrete fourier transformer
    """
    N = len(f)
    if not check_power2(N):
        raise ValueError("f length is not power of 2")
    l = get_bit(N)
    # re-arange ts by flipping bits
    F = np.zeros(N, dtype=np.complex)
    for i, a in enumerate(f):
        F[flip_bits(i, l-1)] = a
    
    factor = lambda x, a: x*a
    if reverse:
        factor = lambda x, a: x/a

    step = 1
    cnt = 1
    while step < n:
        for i in range(0, N, 2*step):
            w = 1.0
            for j in range(i, i+step): 
                # butterfly transform
                a = F[j] + w*F[j+step]
                b = F[j] - w*F[j+step]
                w = factor(w, WNK[cnt])
                F[j] = a
                F[j+step] = b 
        step *= 2
        cnt += 1 
    
    return F/N if reverse else F

4.多项式乘法与FFT

使用fft可以加速多项式乘法。首先，\(n\)次多项式\(f(x)\)的定义如下，
\[f(x)=a_{0}+a_{1}x^{1}+a_{2}x*{2}+\dots+a_{n}x^{n}\]
类似地，有\(n\)次多项式\(g(x)\)，
\[g(x)=b_{0}+b_{1}x^{1}+b_{2}x*{2}+\dots+b_{n}x^{n}\]
一般情况下，我们使用嵌套遍历来计算\(f(x)g(x)\)，代码（python）如下

def poly(ar, br):
    """ defatul polynomial multiplication: n*n
    """
    n = len(ar)
    cr = np.zeros(2*n-1)
    for i, a in enumerate(ar):
        for j, b in enumerate(br):
            cr[i+j] += a*b
    return cr

\(f(x)g(x)\)的时间复杂度是\(O(n^{2})\)，使用傅里叶变换可以优化\(f(x)g(x)\)（复杂度降至\(O(n\log{n})\)）。思路是：

  1. \(f(x)\)通过傅里叶变换得到\(F(x)\), \(g(x)\)通过傅里叶变换得到\(G(x)\)
  2. \(F(x)\)和\(G(x)\)的对应项相乘，得到\(H(x)\)
  3. \(H(x)\)使用傅里叶逆变换得到\(h(x)\)

则\(h(x)=f(x)g(x)\)，上式过程在理论上应该是成立的（具体数学证明请另外搜索相关资料），具体的代码（python）如下：

def poly_fft(ar, br):
    """ polynomial multiplication by fft: nlogn 
    """
    n = len(ar) # assume ar.length == br.length and ar.length is power of 2
    padded = np.zeros(n) # pad to 2n
    far = fft(np.append(ar, padded))
    fbr = fft(np.append(br, padded))
    fcr = far * fbr
    cr = np.array([x.real for x in ifft(fcr)])
    return cr[:-1]

fft和ifft的时间复杂度是\(O(n\log{n})\)，我们用fft做多项式乘法时，做了3次变换，一次向量乘法，因此时间复杂度为\(O(n\log{n})\)。可以用简单的实验对比一下两种方法的效率（fft和ifft是我们之前实现的），代码（python）如下

import cmath
import functools
import time
import numpy as np

def timer(func):
    @functools.wraps(func)
    def func_with_timer(*args, **kwargs):
        start = time.time()
        res = func(*args, **kwargs)
        end = time.time()
        print(f"{func.__name__} cost {end - start} seconds")
        return res
    return func_with_timer

@timer
def poly_fft(ar, br):
    """ polynomial multiplication by fft: nlogn 
    """
    n = len(ar) # assume ar.length == br.length and ar.length is power of 2
    padded = np.zeros(n) # pad to 2n
    far = fft(np.append(ar, padded))
    fbr = fft(np.append(br, padded))
    fcr = far * fbr
    cr = np.array([x.real for x in ifft(fcr)])
    return cr[:-1]

@timer
def poly(ar, br):
    """ defatul polynomial multiplication: n*n
    """
    n = len(ar)
    cr = np.zeros(2*n-1)
    for i, a in enumerate(ar):
        for j, b in enumerate(br):
            cr[i+j] += a*b
    return cr

if __name__ == '__main__':
    n = 1024
    f = np.ones(n)
    g = np.ones(n) * 2.0
    p = poly(f, g)
    fp = poly_fft(f, g)
    for i in range(int(n*0.1)):
        print(p[i], fp[i])

取\(n=1024\)时，对比结果如下：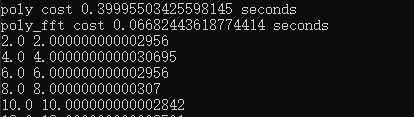
对比结果

从结果上看，使用fft的确要效率更高，而且二者的计算结果基本一样。

5.总结

对fft的介绍就到这里为止了，由于本人对傅里叶变换的了解不多，应用也比较少，所以只能从算法角度来谈谈个人对fft的认识，并总结一些可能比较重要的细节，希望能够为读者提供帮助和参考价值。另外，本文的公式和代码比较多，存在错误，烦请指出，谢谢！

标签
fft
快速傅里叶变换
dft
bit
易学教程内所有资源均来自网络或用户发布的内容，如有违反法律规定的内容欢迎反馈！
该文章没有解决你所遇到的问题?点击提问,说说你的问题,让更多的人一起探讨吧!