距离相关系数:
线性关系可以通过pearson相关系数来描述,单调关系可以通过spearman或者kendall来描述,非线性如何描述,距离相关系数可以非线性相关性。
我们都知道,皮尔森关联系数只能描述数据键的线性相关性程度,对于非线性相关数据,皮尔森关联系数显然不适合的,距离相关系数恰恰能在很大程度上客服皮尔森相关系数的弱点。
比如:Pearson相关系数等于0,这两个变量并不一定就是独立的(有可能是非线性相关);但如果距离相关系数为0的话,那么就可以说这两个变量是独立的了。
距离相关系数的计算依赖于距离协方差和距离方差,首先我们先了解下距离协方差的定义,假设有n维(X,Y)统计样本。
- 首先计算包含的所有成对距离(即:数组间每行数据之间的范数距离)

为了防止我没有描述清楚,直接上代码:
#生成一个3行2列的数组
X = np.random.randint(-100,100,(3,2))0.1
out:array([[ 4.8, 7.7],
[-2.6, 6.8],
[ 5.9, 9. ]])
Y = X**2
#取数据集的行
col = X.shape[0]
#做成nn的零矩阵,用于盛放数据
a = np.zeros((col,col))
b = np.zeros((col,col))
A = np.zeros((col,col))
B = np.zeros((col,col))
#计算数组间每行数据之间的范数距离
for j in range(col):
for k in range(col):
a[j,k] = np.linalg.norm(X[j]-X[k])
b[j,k] = np.linalg.norm(Y[j]-Y[k])
部分打印信息:
调试: X数据集索引为0的数据与索引为0的数据的范数距离为0
计算a列之间的距离: 0.0
计算b列之间的距离: 0.0
调试: X数据集索引为0的数据与索引为1的数据的范数距离为.
计算a列之间的距离: 8.174350127074325
计算b列之间的距离: 25.112168365157167
调试: X数据集索引为0的数据与索引为2的数据的范数距离为.
计算a列之间的距离: 8.229823813423955
计算b列之间的距离: 71.77571803890227
。。。这里的a和b最后生成的都是对称矩阵 - 然后对所有的成对距离进行中心化处理
 其中aj. 是第j行平均值,ak.是第k列平均值,a…是X样本的距离矩阵的平均值
其中aj. 是第j行平均值,ak.是第k列平均值,a…是X样本的距离矩阵的平均值
代码:
for m in range(col):
for n in range(col):
#计算a,b中心化的值,并赋值给A,B
A[m,n] = a[m,n] - a[m].mean()-a[:,n].mean()+a.mean()
B[m,n] = b[m,n] - a[m].mean()-b[:,n].mean()+b.mean() - 计算样本距离的平方协方差(标量)的算数平均:
 cov_xy=np.sqrt((1/(col**2))((AB).sum()))
cov_xy=np.sqrt((1/(col**2))((AB).sum())) - 计算样本距离方差
 cov_xx=np.sqrt((1/(col2))((AA).sum()))
cov_xx=np.sqrt((1/(col2))((AA).sum()))
cov_yy=np.sqrt((1/(col2))((BB).sum())) - 将两个随机变量的距离协方差除以它们的距离标准差的乘积,得到它们的距离相关性,即:
 dcor = cov_xy/np.sqrt(cov_xx*cov_yy)
dcor = cov_xy/np.sqrt(cov_xx*cov_yy)
#写成函数形式如下:
import numpy as np
import pandas as pd
def dist_corr(x,y):#如果x,y是二维数组,应通过行矢量形成距离矩阵
#获取数据集的行
col=x.shape[0]
#生成a、b、A、B三个colcol的0矩阵
a=np.zeros((col,col))
b=np.zeros((col,col))
A=np.zeros((col,col))
B=np.zeros((col,col))
#通过双层循环计算出列之间的范数距离
for j in range(col):
for k in range(col):
#求范数
a[j,k]=linalg.norm(x[j]-x[k])
b[j,k]=linalg.norm(y[j]-y[k])
#print(a,b)
#通过循环对其进行中心化处理
for m in range(col):
for n in range(col):
A[m,n]=a[m,n]-a[m].mean()-a[:,n].mean()+a.mean()
B[m,n]=b[m,n]-b[m].mean()-b[:,n].mean()+b.mean()
#求协方差
cov_xy=np.sqrt((1/(col**2))((AB).sum()))
cov_xx=np.sqrt((1/(col**2))((AA).sum()))
cov_yy=np.sqrt((1/(col**2))((BB).sum()))
return cov_xy/np.sqrt(cov_xxcov_yy)
来源:CSDN
作者:轻轻一point
链接:https://blog.csdn.net/qq_41675973/article/details/103585695
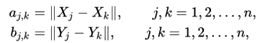
 其中aj. 是第j行平均值,ak.是第k列平均值,a…是X样本的距离矩阵的平均值
其中aj. 是第j行平均值,ak.是第k列平均值,a…是X样本的距离矩阵的平均值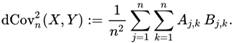 cov_xy=np.sqrt((1/(col**2))((AB).sum()))
cov_xy=np.sqrt((1/(col**2))((AB).sum()))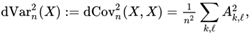 cov_xx=np.sqrt((1/(col2))((AA).sum()))
cov_xx=np.sqrt((1/(col2))((AA).sum()))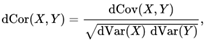 dcor = cov_xy/np.sqrt(cov_xx*cov_yy)
dcor = cov_xy/np.sqrt(cov_xx*cov_yy)