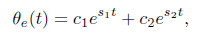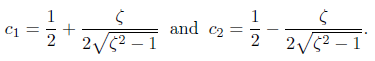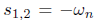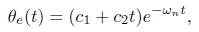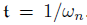本节主要回顾二阶系统的控制理论,枯燥
本节我们关注单个关节的控制动力学,多个关节的控制只是单关节的简单延申。
假设期望的位置为 θd(t),实际关节位置为 θ(t) ,那么我们定义关节误差为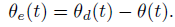
描述控制系统的 θe(t) 演变的差分方程被称为误差动力学(error dynamics)。反馈控制器的目的就是通过调整控制器创造出一个 θe(t) 随着时间变化趋于0的一个系统。
如果存在对于一些初始条件下,随着t趋于无穷大,︱θe(t)︱没有界,则称该误差动力学不稳定。如果对于任意初始条件 θe(t) 收敛,则称该误差动力学稳定。稳定是一个控制器最基本的要求。
11.2.1误差响应
要测试一个控制器的好坏,一个常规方法是引入一个干扰带来一个非0的初始误差 θe(0) ,然后看控制器能多快把误差降到0。我们规定:对于初始条件 θe(0)=1,t>0 时控制系统的响应 θe(t)被称为误差响应。并且 θe(t) 在 t=0 时的任意阶微分都要为0。
一个理想的控制器会快速地把误差控制到 0 并且一直将误差维持在 0 。在实际情况下,减少误差是需要时间的,而且误差有时没有办法完全消除。如下图所示: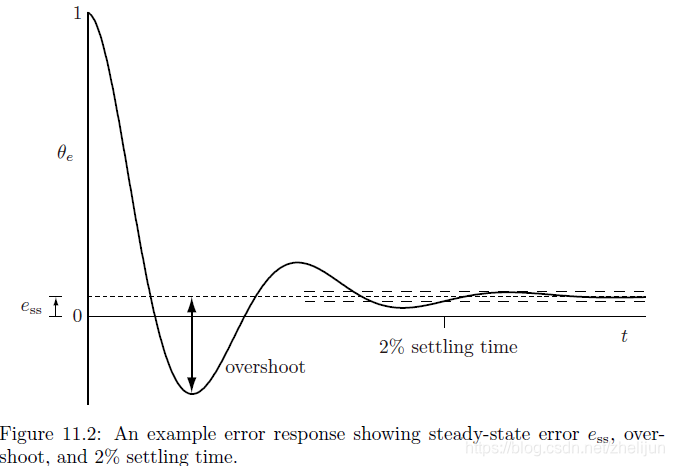
误差响应 θe(t) 可以用瞬时响应和稳态响应来刻画。稳态响应用稳态误差ess来描述,定义为当t趋于无穷大的时候的渐进误差。瞬时响应用超调和稳定时间(2%)来刻画,这里的2%指的是系统在趋于稳定的过程中,第一次满足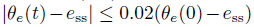
,并且此后的误差统统小于这里的2%所用的时间。超调则指误差响应首次超过稳态误差的大小,定义为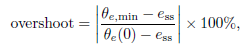
这里的 θe,min 是 the least positive value achieved by the error。
一个好的误差响应应该满足以下条件:
- 稳态误差很小或者为0
- 超调很小或者为0
- 稳定时间很短
11.2.2 线性误差动力学
本节我们主要讨论误差动力学由以下线性常微分方程描述的线性系统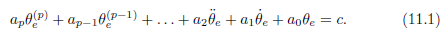
这是一个p阶差分方程,如果常量 c = 0,那么该差分方程为齐次方程,c不为0则是非齐次差分方程。对于差分方程为齐次方程的误差动力学,差分方程可以改写为: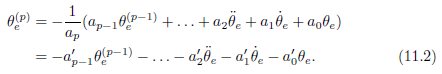
我们定义
其中
那么11.2式变为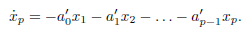
于是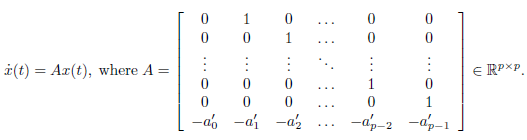
对于一阶差分方程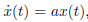
有解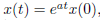
由此类推,对于向量差分方程,如果满足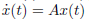
有解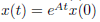
再由标量差分方程在a小于0的情况下,无论初始条件如何,其根 x 都收敛于 0,类推得到对于方程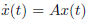
如果A是负定矩阵,且根收敛于0,那么A的特征值具有负的实部。A的特征根是通过其特征多项式的根求出来的,s域下满足: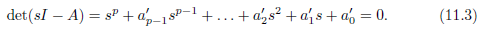
该方程同时也是 p 阶差分方程 式 (11.1) 的特征方程。
使上述特征方程全部根都具有负的实部,也就是使具有该特征方程的误差动力学稳定的一个必要条件是:
所有的系数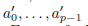
必须为正,这个条件对于p = 1,2 成立。对于p = 3,还必须满足: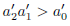
对于再高阶的情况,还有其他条件需要满足。
对于二阶的误差动力学,大都可以类比为一个典型质量-弹簧-阻尼模型,结构示意图如下: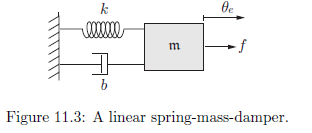
质量块m的位置记为 θe,有一个外力f作用在质量块上。阻尼器对质量块施加了一个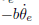
的力,b 是它的阻尼系数,弹簧对质量块施加了-kθe 的力,k 是弹力系数。因此该系统的运动方程可以表示为:
假如质量块为0,那么方程变形为:
这是一个一阶的动力学公式,f 只引起速度而不是加速度。
在接下来的部分我们将会研究当 f = 0,且 b,k>0 时的一阶和二阶误差响应,确保误差动力学稳定并且误差收敛于0。
11.2.2.1 一阶误差动力学
一阶误差动力学在f=0时,其动力学公式可以表示为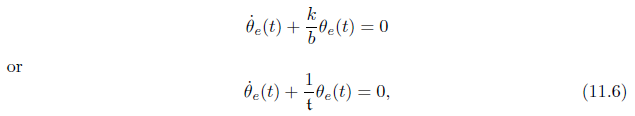
这里t=b/k被称之为一阶差分方程的时间常量,该方程的解为
时间常量t的物理意义是,该系统的解衰减至其初值的37%所需要耗费的时间。误差动力学的初值由初值条件定义为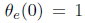
下图展示了对于不同时间常数误差响应的变化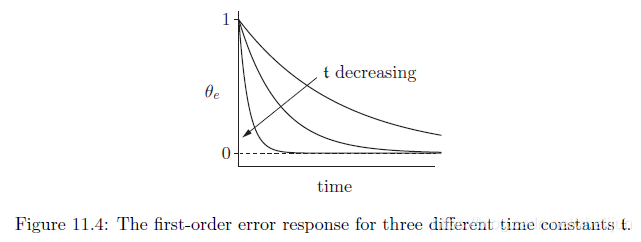
对于此系统,稳态误差为0,没有超调,稳定时间的求法为: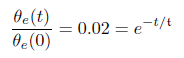
求解得到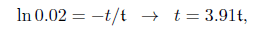
由此可知系统响应随着 k 增加或者 b 减少而变快。
11.2.2.2二阶误差动力学
二阶误差动力学公式为: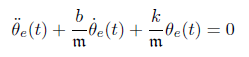
写成标准形式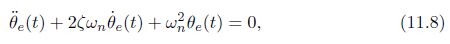
wn被称之为自然频率,ζ被称之为阻尼比。对于质量-弹簧-阻尼系统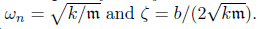
并且特征方程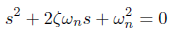
的根为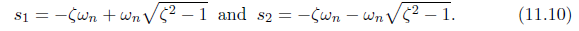
当且仅当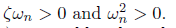
时该误差动力学稳定。如果某二阶误差动力学稳定,那么根据ζ的不同值,系统的响应可分为以下三种情况:
- 过阻尼:ζ>1. 特征方程有两个不同的实根s1和s2。差分方程的解为

c1 和 c2 可以根据初始条件计算出来。该响应是两个递减的指数的和,并且t1 = -1/s1,t2 = -1/s2。单位误差响应的初始条件是 θe(0) = 1 以及 θe(0) 的导数 = 0,c1 和 c2 的值为:
- 临界阻尼:ζ=1。特征方程有两个一样的实根

解为
该解为一个线性的部分乘递减的指数部分,衰减指数部分的时间常量
对于该误差响应
因此:
后面我翻译不下去了



来源:CSDN
作者:呜啦呜啦呜啦呜啦
链接:https://blog.csdn.net/zhelijun/article/details/101456338