数据清洗和特征选择

数据清洗

清洗过程

数据预处理：
- 选择数据处理工具：数据库、Python相应的包；
- 查看数据的元数据及数据特征；
清理异常样本数据：
- 处理格式或者内容错误的数据；
- 处理逻辑错误数据：数据去重，去除/替换不合理的值，去除/重构不可靠的字段值；
- 处理不需要的数据：在进行该过程时，要注意备份原始数据；
- 处理关联性验证错误的数据：常应用于多数据源合并的过程中。
采样：
- 数据不均衡处理：上采样、下采样、SMOTE算法
- 样本的权重问题

数据不平衡

在实际应用中，数据的分布往往是不均匀的，会出现"长尾现象"，即绝大多数的数据在一个范围/属于一个类别，而在另外一个范围或者类别中，只有很少一部分数据。此时直接采用机器学习效果不会很好，因此需要对数据进行转换操作。

长尾效应：

解决方案01

设置损失函数的权重，使得少数类别数据判断错误的损失大于多数类别数据判断错误的损失，即：当我们的少数类别数据预测错误的时候，会产生一个比较大的损失值，从而导致模型参数往让少数类别数据预测准确的方向偏。

可通过设置sklearn中的class_weight参数来设置权重。

解决方案02

下采样/欠采样(under sampling)：从多数类中随机抽取样本从而减少多数类别样本数据，使数据达到平衡的方式。

集成下采样/欠采样：采用普通的下采样方式会导致信息丢失，所以一般采用集成学习和下采样结合的方式来解决问题，主要有以下两种方式：

EasyEnsemble：采用不放回的数据抽取方式抽取多数类别样本数据，然后将抽取出来的数据和少数类别数据组合训练一个模型；进行多次操作，构建多个模型，然后使用多个模型共同决策/预测。
BalanceCascade：利用Boosting增量思想来训练模型；先通过下采样产生训练数据，然后使用Adaboost算法训练一个分类器，使用训练好的分类器对所有的样本数据进行预测，并将预测正确的样本从大众样本中删除；重复迭代上述两操作，直到大众样本数据量等于小众样本数据量。

解决方案03

Edited Nearest Neighbor(ENN)：对于多数类别样本数据而言，如果这个样本的大部分k近邻样本都和自身类别不一样，那么就将其删除，然后使用删除后的数据进行模型训练。

Repeated Edited Nearest Neighbor(RENN)：重复上述ENN的步骤，直到数据集无法再被删除后，使用此时的数据集进行模型训练。

解决方案04

Tomek Link Removal：如果两个不同的类别，它们的最近邻都是对方，即A的最近邻是B，B的最近邻是A，那么A和B就是Tomek Link。将所有Tomek Link中多数类别的样本删除，然后使用删除后的样本进行模型训练。

解决方案05

过采样/上采样(Over Sampling)：和欠采样采用同样的原理，通过抽样来增加少数样本的数目，从而达到数据平衡的目的。

一种简单的方式就是通过有放回抽样，不断的从少数类别样本数据中抽取样本，然后使用抽取样本+原始数据组成训练数据来训练模型；该方式比较容易导致过拟合，一般抽样样本不要超过50%;
由于在上采样过程中，是进行随机有放回抽样，因此在最终模型中，数据会存在重复性，通过加入一定的随机性进行避免，即：在抽取数据后，对数据的各个维度可以进行小范围变动

eg：(1, 2, 3)->(1.01, 1.99, 3.02)

解决方案06

采用数据合成的方式生成更多的样本，该方式在小数据集场景下具有比较成功的案例。常见的SMOTE算法，利用小众样本在特征空间的相似性来生成新样本。

传送门：SMOTE算法Python实现

解决方案07

对于正负样本极不平衡的情况下，其实可以换一种角度来看待这个问题：

可以将其看成一分类(One Class Learning)或者异常检测(Novelty Detection)问题，在这类算法应用中主要就是对于其中一个类别进行建模，然后对所有不属于这个类别特征的数据就认为是异常数据，经典算法包括：One Class SVM、IsolationForest等。

特征转换

特征转换主要指将原始数据中的字段数据进行转换操作，从而得到适合进行算法模型构建的输入数据(数值型数据)，在这个过程中主要包括但不限于以下几种数据的处理：

文本数据转换为数值型数据
缺失值填充
定性特征属性亚编码
定量特征属性二值化
特征标准化与归一化

文本数据转换为数值型数据

在对文本数据进行处理前，需要进行对文本数据的分词操作。

目前常见的中文分词工具有：GitHub:jieba

机器学习的模型算法均要求输入的数据必须是数值型的，所以对于文本类型的特征属性，需要进行文本数据转换，也就是需要将文本数据转换为数值型数据。常用方式如下：

词袋法(BOW)
TF-IDF(Item frequency-inverse document frequency)
HashTF
Word2Vec(主要用于单词的相似性考量)

词袋法/词集法

Bag of words，该模型忽略文本的语法和语序，用一组无序的单词(words)来表达一段文字或者一个文档，词袋法中使用单词在文档中出现的次数(频数)来表示文档。

eg：

d1: this is a sample is a sample

d2: this is another example another example

dict: this sample another example

this sample another example
d1 1 2 0 0
d2 1 0 2 2

	this	sample	another	example
d1	1	2	0	0
d2	1	0	2	2

Set of words，为词袋法的变种，和词袋法的区别在于：词袋法使用的是单词的频数，而词集法中使用的是单词是否出现，如出现则赋值1，否则赋值0.

TF-IDF

在用词袋法是，没有考虑到单词的重要性，不同的单词对于文本而言其重要性是不同的，对于单词对文本的重要性评估方式如下：

单词的重要性随着它在文本中出现的次数成正比增加，也就是单词的出现次数越多，该单词对于文本的重要性就越高
单词的重要性会随着在语料库中出现的频率成反比下降，也就是单词在语料库中出现的频率越高，表示该单词与常见，也就是该单词对于文本的重要性越低

TF-IDF(Item frequency-inverse document frequency)是一种常用的用于信息检索与数据挖掘的常用加权技术

TF-Item frequency：词频
IDF-Inverse document frequency：逆文档频率

\[ 假设：单词用t表示，文档用d表示，语料库用D表示，|D|表示文档数量，|d|表示文档d所有单词数量； \]

\[ N(t, D)表示包含单词t的文档数量，N(t,d)表示在文档d中单词t出现的次数 \]

\[ TFIDF(t, d, D)=TF(t,d) \times IDF(t, D) \]

\[ TF(t, d)=\frac{N(t, d)}{|d|}~~~~~~~IDF(t, D)=log[\frac{|D|+1}{N(t, D)+1}] \]

TF-IDF除了使用上述默认的计算公式外，还有其他变种的计算公式。

Hash Trick

前面的词袋法，或者是TF-IDF，都需要计算文档中单词的词频；在文档数量比较少，单词数量比较少的时候，计算量不会太大，而当文档的数量上升到一定程度的到时候，程序的计算效率就会下降，此时就可以通过Hash Trick的形式解决该问题。

在Hash Trick里，通过定义一个特征Hash后对应的哈希表的大小，这个哈希表的维度会远远小于我们的词汇表的特征维度，因此可以看成是降维。具体的方法是，对应任意一个特征名，我们会用Hash函数找到对应哈希表的位置，然后将该特征名对应的词频统计值累加到该哈希表位置。
\[ 假设：Hash函数h使第i个特征Hash到位置j，即h(i)=j, \]

\[ 则第i个原始特征的词频数值ϕ(i)将累加到Hash后的第j个特征的词频数值\overline{ϕ}，如下 \]

\[ \overline{ϕ}(j)=\sum_{i∈J;h(i)=j}{ϕ(i)},J为原始的特征维度 \]

Hash Trick的计算规则是：在计算过程中，不计算词频，而是计算单词进行hash后的hash值数量；

Hash Trick特点：运行速度快，但是无法获取高频词，有可能存在单词碰撞问题(hash值一样)

解决方式：hash Trick的变种signed hash trick

参考：文本挖掘预处理之向量化与Hash Trick-3. Hash Trick

Word2Vec

Word2Vec，Word Embeddings，"词向量"，作用是将自然语言中的词语转换为机器学习可以理解的稠密向量(Dense Vector)，Word2Vec是One-Hot Encoder更进一步的表现形式。

使用One-Hot Encoder来实现词向量的话，向量中只有一个值为1，其他值均为0，存在两个问题：

编码随机，向量之间相互独立；
矩阵过于稀疏，可能会出现维度灾难；

而Word2Vec可以将One-Hot Encoder转换为低纬度的连续值，也就是稠密向量，并将相近的词映到向量空间相似的位置中。

Word2Vec主要分为CBOW(Continuous Bag of Words)和Skip-Gram两种模型：

CBOW是从原始语句推测目标字词，适合小型规模的数据集；
Skip-Gram是从目标字词推测原始语句，适合大型语料库上的模型构建。

对于同样的一个句子：Shanghai is a nice city。我们需要构建一个语境和词汇之间的映射关系，其实就是input和label之间的关系。

CBOW构造出来的映射关系为(窗口为1)：(Shanghai, a) -> is, (is, nice) -> a,(a, city) -> nice

Skip-Gram构造出来的映射关系为(窗口为1)：(is, Shanghai), (a, is), (nice, a), (city, nice), (Shanghai, is), (a, is), (a, nice), (nice, city)

通过Word2Vec的构建，最终得到的词向量，会将比较相似的单词放在样本空间中比较接近的位置，那么基于这样一个信息，可以得到文档中单词与单词之间的相关性。

缺省值填充

缺省值是数据中最常见的一个问题，处理缺省值有很多方式，主要包括以下四个步骤进行缺省值处理：

确定缺省值范围
去除不需要的字段

在进行去除不需要的字段的时候，需要注意的是：删除操作最好不要直接操作与原始数据上，最好的是抽取部分数据进行删除字段后的模型构建，查看模型效果，如果效果不错，那么再到全量数据上进行删除字段操作。总而言之：该过程简单但是必须慎用，不过一般效果不错，删除一些丢失率高以及重要性低的数据可以降低模型的训练复杂度，同时又不会降低模型的效果。

填充缺省值内容

填充缺省值内容是一个比较重要的过程，也是我们常用的一种缺省值解决方案，一般采用下面几种方式进行数据的填充

以业务知识或经验推测填充缺省值

以同一字段指标的计算结果(均值、中位数、众数等)填充缺省值

以不同字段指标的计算结果来推测性的填充缺省值，比如通过身份证号码计算年龄、通过收货地址来推测家庭住址、通过访问的IP地址来推测家庭/公司/学校的家庭住址等等

重新获取数据

亚编码

OneHotEncoder，对于定性的数据(也就是分类的数据)，可以采用N位的状态寄存器来对N个状态进行编码，每个状态都有一个独立的寄存器位，并且在任意状态下只有一位有效；是一种常用的将特征数字化的方式。比如有一个特征属性:['male','female']，那么male使用向量[1,0]表示，female使用[0,1]表示。

二值化

二值化(Binarizer)：对于定量的数据（特征取值连续）根据给定的阈值，将其进行转换，如果大于阈值，那么赋值为1；否则赋值为0.

数据多项式扩充变换

多项式数据变换主要是指基于输入的特征数据按照既定的多项式规则构建更多的输出特征属性，比如输入特征属性为[a,b]，当设置degree为2的时候，那么输出的多项式特征为[1, a, b, a^2, ab, b^2]；

从低维空间映射到多维空间，将非线性的数据转换为线性可分的数据。

其他特征转换

标准化

基于特征属性的数据(也就是特征矩阵的列)，获取均值和方差，然后将特征值转换至服从标准正态分布。计算公式如下：
\[ x'=\frac{x-\overline{X}}{S} \]

注：改变了数据的分布

归一化

即区间缩放法，是指按照数据的取值范围特性对数据进行缩放操作，将数据缩放到给定区间上，常用的计算方式如下：
\[ X\_std=\frac{X-X.min}{X.max-X.min}~~~~~~~~X\_scaled=X\_std*(Def.max-Def.min)+Def.min \]

其中Def表示给定的区间

正则化

和标准化不同，正则化是基于矩阵的行进行数据处理，其目的是将矩阵的行均转换为“单位向量”，l2规则转换公式如下：
\[ x' = \frac{x}{\sqrt{\sum_{j=1}^{m}{x(j)^2}}} \]

总结

标准化的目的是为了降低不同特征的不同范围的取值对于模型训练的影响；通过标准化改变数据的分布特征，具有以下两个好处：1. 提高迭代求解的收敛速度；2. 提高迭代求解的精度。

归一化对于不同特征维度的伸缩变换的主要目的是为了使得不同维度度量之间特征具有可比性，同时不改变原始数据的分布(相同特性的特征转换后，还是具有相同特性)。和标准化一样，也属于一种无量纲化的操作方式。

正则化则是通过范数规则来约束特征属性，通过正则化我们可以降低数据训练处来的模型的过拟合可能，和之前在机器学习中所讲述的L1、L2正则的效果一样。在进行正则化操作的过程中，不会改变数据的分布情况，但是会改变数据特征之间的相关特性。

特征选择

当做完特征转换后，对于存在的多种特征属性，可能会存在过多的特征属性导致模型构建效率降低，同时模型的效果可能会变的不好，那么此时就需要从这些特征属性中选择出影响最大的特征属性作为最后构建模型的特征属性列表。

在选择模型的过程中，通常从两个方面来选择特征：

特征是否发散：若一个特征不发散，比如方差接近于0，即此时的特征对于样本的区分没什么作用；
特征与目标的相关性：如果特征与目标的相关性比较高，应当优先选择

特征选择方法主要有以下三种：

Filter：过滤法，按照发散性或者相关性对各个特征进行评分，设定阈值进行特征选择；常用的方法包括方差选择法，相关系数法，卡方检验，互信息法；
Wrapper：包装法，根据目标函数(通常是预测效果评分)，每次选择若干特征或者排除若干特征；常用方法主要是递归特征消除法；
Embedded：嵌入法，先使用某些机器学习的算法和模型进行训练，得到各个特征的权重系数，根据系数从大到小选择特征；常用方法主要是基于惩罚项的特征选择法。

过滤法Filter

方差选择法：先计算各个特征属性的方差值，然后根据阈值，获取方差大于阈值的特征
相关系数法：先计算各个特征属性对于目标值的相关系数以及阈值K，然后获取K个相关系数最大的特征属性

需要根据目标属性y的类别选择不同的方式
卡方检验：检查定性自变量对定性因变量的相关性
\[ χ^2=\sum{\frac{(A-E)^2}{E}} \]

\[ 其中：A-实际值，T-理论值 \]

推荐：了解什么是卡方检验

包装法Wrapper

递归特征消除法：使用一个基模型来进行多轮训练，每轮训练后，消除若干权值系数的特征，在基于新的特征集进行下一轮训练。

嵌入法Embedded

基于惩罚项的特征选择法：在使用惩罚项的及模型，除了可以筛选出特征外，同时还可以进行降维操作。

基于树模型的特征选择法：树模型中GBDT在构建的过程会对特征属性进行权重的给定，所以GBDT也可以应用在基模型中进行特征选择。

降维

当特征选择完成后，可以直接可以进行训练模型了，但是可能由于特征矩阵过大，导致计算量比较大，训练时间长的问题，因此降低特征矩阵维度也是必不可少的。

常见的降维方法除了基于L1的惩罚模型外，还有主成分析(PCA)和线性判别分析法(LDA)，这两种方法的本质都是将原始数据映射到维度更低的样本空间中；但是采用的方式不同，PCA是为了让映射后的样本具有更大的发散性，LDA是为了让映射后的样本有最好的分类性能。

除了使用PCA和LDA降维外，还可以使用主题模型来达到降维的效果

在实际的机器学习项目中，降维一般而言是必须进行的，因为数据中存在以下几个方面的问题：

数据的多重共线性：特征属性之间存在着相互关联关系，多重共线性会导致解的空间不稳定，从而导致模型的泛华能力弱；
高维空间样本具有稀疏性，导致模型比较难找到数据特征；
过多的变量会妨碍模型查找规律；
仅仅考虑单个变量对于目标属性的影响可能忽略变量之间的潜在关系

通过降维的目的：

减少特征属性的个数；
确保特征属性之间是相互独立的。

主成分分析

主成分分析，PCA：将高维的特征向量合并成为低纬度的特征属性，是一种无监督的降维方法。

PCA原理

PCA(Principal Component Analysis)是常用的线性降维方法，是一种无监督的降维算法。算法目标是通过某种线性投影，将高维的数据映射到低维空间中表示，并且期望在所投影的维度上数据的方差最大，以此使用较少的数据维度，同时保留较多的原数据点的特性。

通俗来讲，如果将所有点都映射到一起，那么维度一定会下降，但是同时会丢失几乎所有的信息，而如果在映射之后数据还具有较大的方差，即数据点还是较分散，那样的话就可以保存更多的信息。从而我们可以看到PCA是一种丢失原始数据信息最少的无监督线性降维方式。

在PCA降维中，数据从原来的坐标系转换为新的坐标系，新坐标系的选择有数据本身的特征决定：

第一个坐标轴选择原始数据中方差最大的方向；
第二个坐标轴选择和第一个坐标轴垂直或者正交的方向；
第三个坐标轴选择和第一个、第二个坐标轴都垂直或者正交的方向。
一直重复上述过程，直到新坐标系的维度和原始坐标系维度数目一致时结束计算。

推导过程

\[ 现有样本X，已经经过中心化，每列表示一个样本，每行表示一个特征(为了方便，和之前设置不同) \]

\[ 再设：样本点x_i在新空间的超平面上的投影是：W^Tx_i \]

\[ 若所有样本点的投影能尽可能的分开，则表示投影之后的点在各个维度上的方差应该最大化 \]

\[ 那么投影样本点的各个维度方差和可以表示为：\frac{1}{n}\sum_i{W^Tx_i(W^Tx_i)^T}=\frac{1}{n}\sum_i{W^Tx_ix_i^TW^T} \]

\[ 若有已经经过中心化后的特征x_k=(-2,1,1),其均值已经为0，则其方差为： \]

\[ x_k \cdot x_k^T= (-2)^2+1^2+1^2 \]

\[ 从而我们可以得到PCA的最优目标函数是：max_Wtr(W^TXX^TW) \]

\[ 其中：s.t. W^TW=I(由于每个坐标轴都是正交)，tr表示矩阵的迹 \]

\[ 在PCA得出上述PCA目标函数的基础上，代入拉格朗日求解，可以得到最终的拉格朗日函数为： \]

\[ L=W^TXX^TW+λ(I-W^TW) \]

\[ 对上述拉格朗日求偏导：\frac{∂L}{∂W}=2XX^TW-2λW \]

\[ 令其\frac{∂L}{∂W}=0⇒XX^TW=λW⇒λ=W^TXX^TW \]

\[ 将XX^T看成一个整体A，那么求解W的过程矩阵A的特征向量的过程 \]

因此PCA的计算过程本质为对去中心化的数据的协方差矩阵求解特征值和特征向量。

PCA执行过程

输入：
\[ 样本集X=\{x_1,x_2,...,x_n \},每个样本有m维特征，X是一个m行n列的矩阵 \]
步骤：

数据中心化：对X中的每一行(即一个特征属性)进行零均值化，即减去这一行的均值；
求出数据中心化后矩阵X的协方差矩阵(即特征与特征之间的协方差构成的矩阵)；
求解协方差矩阵的特征值和特征向量;

1.协方差矩阵的计算及意义

2.在求解时，可以通过SVD对矩形进行分解来简化求解过程
将特征向量按照特征值从大到小按列进行排列，获取最前面的k列数据形成矩阵W；
利用矩阵W和样本集X进行矩阵的乘法得到降低到k维的最终数据矩阵。

PCA案例：
\[ 现有5条案例：\left[ \begin{matrix} 1 & 1 & 2 & 4 & 2\\ 1 & 3 & 3 & 4 & 4 \end{matrix} \right]⇒_{中心化}\left[ \begin{matrix} -1 & -1 & 0 & 2 & 0\\ -2 & 0 & 0 & 1 & 1 \end{matrix} \right] \]

\[ 计算协方差矩阵：cov=\frac{1}{m-1}XX^T=\left[ \begin{matrix} 1.5 & 1\\ 1 & 1.5\end{matrix} \right] \]

\[ 计算协方差矩阵cov的特征值和特征向量：\begin{cases} λ_1=0.5\\ λ_2=2.5\end{cases}⇒\begin{cases} w_1=[\frac{-1}{\sqrt2}~~~~\frac{1}{\sqrt2}]^T\\ w_2=[\frac{1}{\sqrt2}~~~~\frac{1}{\sqrt2}]^T\end{cases} \]

\[ X'=W^TX=\left[ \begin{matrix} \frac{1}{\sqrt2} & \frac{1}{\sqrt2}\\ \frac{-1}{\sqrt2} & \frac{1}{\sqrt2}\end{matrix} \right] \cdot \left[ \begin{matrix} -1 & -1 & 0 & 2 & 0\\ -2 & 0 & 0 & 1 & 1 \end{matrix} \right]=\left[ \begin{matrix} \frac{-3}{\sqrt2} & \frac{-1}{\sqrt2} & 0 & \frac{3}{\sqrt2} & \frac{1}{\sqrt2}\end{matrix} \right] \]

线性判断分析

LDA，Linear Discriminate Analysis，LDA是一种基于分类模型进行特征属性合并的操作，是一种有监督的降维方法。

LDA的原理：将带标签的数据点，通过投影的方法，投影到维度更低的空间中，使得投影后的点，会形成按类别区分，一簇一簇的情况，相同类别的点，将会在投影后的空间中更接近。

用一句话概括：投影后类内方差最小，类间方差最大。

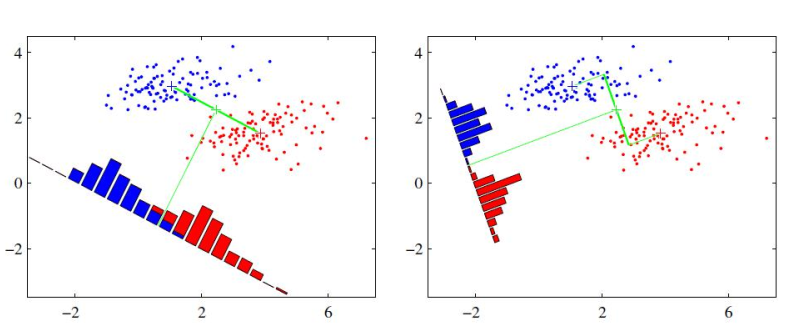
LDA原理

假定转换矩阵为w，那么线性转换函数为：
\[ x'=w^Tx,转换后的数据是一维的 \]

其中x同PCA处相同为列向量

考虑二元分类的情况：认为转换后的值大于某个阈值，属于某个类别;小于等于某个阈值，则属于另一类别。使用类别样本的中心来表示类别信息：
\[ μ_j=\frac{1}{N_j}\sum_{x∈X_j}{x}~~~~~~~~~μ_j’=\frac{1}{N_j}\sum_{x∈X_j}{x'}=\frac{1}{N_j}\sum_{x∈X_j}{w^Tx}=w^Tμ_j \]
那么此时就相当于让这两个中心的距离最远：
\[ J=|μ_1’-μ_2’|=w^T|μ_1-μ_2| \]
同时又要求划分之后通过类别中的样本数据尽可能的接近，也就是痛类别的投影点的协方差要尽可能的小，如下：
\[ Σ_j=\sum_{x∈X_j}{(x-μ_j)(x-μ_j)^T}~~~~~~Σ_j'=\sum_{x∈X_j}{(x'-μ_j')(x'-μ_j')^T}=w^TΣ_jw \]

\[ Σ = Σ_1+Σ_2 \]

结合两者，那么最终的目标函数如下：
\[ max_wJ(w)=\frac{||w^Tμ_1-w^Tμ_2||}{w^TΣ_1w+w^TΣ_2w}=\frac{w^T(μ_1-μ_2)(μ_1-μ_2)^Tw}{w^T(Σ_1+Σ_2)w} \]
最后去使得J极大化的w作为转换矩阵即可，具体的求解方法不再展开。