小结啥啊 很久之前写的 不过现在忘了 来复习一下 不过这种题 不会写暴力 也是很简单啊 但是分少啊qwq
1 欧式距离 也就是我们常说的 欧几里得距离 也就是
$z=\sqrt{x^2+y^2}$ 然后也就是对应到平面上 求两个点的距离的时候 用横纵坐标之差 然后开根号 即可
就是 现在在班里学习文化课 的同学 数学课本上的 计算公式 很好理解 不过 这种一般用于 题目给定你是 这样计算距离
至于 优化 我没见过什么 比较大的优化吧 或许 是我写题少
那么存在一个例题 就是奶酪qwq 奶酪好啊 题目
这里定义了一下 三维平面的计算公式 不过是多了一个维度z 此时距离 我们按照题目给定的计算方法
显然 我们发现这是一个 并查集维护连通性的问题 那么怎么联通 一定是两个球体中心之间的距离 小于等于给定的 2*r 才能相切或者相交
由于我们发现开根号是此类问题的不好处理的地方 那么我们不妨考虑 此时两边平方 即可
#include<bits/stdc++.h>
typedef long long ll;
const ll N=1100;
ll T,n,h,r,x[N],y[N],z[N],father[N],d[N],u[N];
template<typename T>inline void read(T &x)
{
x=0;T f=1,ch=getchar();
while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
while(isdigit(ch)) {x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x*=f;
}
inline long long dis(ll i,ll j) {
return (ll)(x[i]-x[j])*(x[i]-x[j])+(ll)(y[i]-y[j])*(y[i]-y[j])+(ll)(z[i]-z[j])*(z[i]-z[j]);
}
ll fa[N + 5];
ll find(ll x) {
return fa[x]==x?x:fa[x]=find(fa[x]);
}
inline void Union(ll x, ll y) {
fa[find(x)]=find(y);
}
signed main() {
read(T);
while(T--) {
read(n);read(h);read(r);
memset(x,0,sizeof(x));
memset(y,0,sizeof(y));
memset(z,0,sizeof(z));
memset(u,0,sizeof(u));
memset(d,0,sizeof(d));
for(ll i=1;i<=n;++i) fa[i]=i;
for(ll i=1;i<=n;++i) read(x[i]), read(y[i]), read(z[i]);
for(ll i=1;i<=n;++i)
for(ll j=1;j<i;++j)
if(dis(i,j)<=(ll)4*r*r)
Union(i,j);
bool flag=0;
for(ll i=1;i<=n;++i) {
if(z[i]-r<=0) d[find(i)]=1;
if(z[i]+r>=h) u[find(i)]=1;
}
for(int i=1;i<=n;++i)
{
if(d[i]&&u[i])flag=1;
if(flag)break;
}
puts(flag ? "Yes" : "No");
}
return 0;
}
然后就要提到我们的曼哈顿距离了
定义曼哈顿距离是
在二维空间内,两个点之间的曼哈顿距离为它们横坐标之差的绝对值与纵坐标之差的绝对值之和。
设点 A($x_1$,$y_1$) B($x_2$,$y_2$),则 A,B 之间的曼哈顿距离用公式可以表示为:
$d(A,B) = \left | x_1 - x_2\right | + \left | y_1 - y_2 \right |$
对于n维平面的计算公式
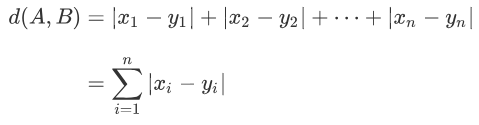
那么我们显然 发现一个东西 这玩意都是非负的 并且自己到自己是0呗(废话
并且 我们发现三个点之间的距离 存在一个三角不等式 d(i,j)≤d(i,k)+d(k,j)
也就是说 在曼哈顿距离的意义下 任意两个点之间的直接距离 不会大于 途径其他点的距离 原来做过一道 图论 就是这样建图的
那么一般是什么问题 计算距离的时候是曼哈顿距离呢?
其实大多是网格图 或者国际象棋。
在国际象棋棋盘上,车从一个格子走到另一个格子的最短距离就是曼哈顿距离。
若网格图上的一个点只能到上下左右 4 个点,且到这 4 个点的距离都相同,则该网格图上两点的距离也为曼哈顿距离。
让你求 若干点对 求 曼哈顿距离 最大的 点对 n是5e4的
根据题意,对于式子$d(A,B) = \left | x_1 - x_2\right | + \left | y_1 - y_2 \right |$ 我们可以分成四种情况考虑:
第一种情况:x1−x2≥0,y1−y2≥0
那么他们之间的距离 就是 x1-x2+y1-y2=(x1+y1)- (x2+y2)
第二种情况 x1−x2<0,y1−y2≥0
那么他们之间的距离 就是 x2-x1+y1-y2=(x2-y2)- (x1-y1)
第三种情况 x1−x2≥0,y1−y2<0
那么他们之间的距离 就是 x1-x2+y2-y1=(x1-y1)- (x2-y2)
第四种情况 x1−x2<0,y1−y2<0
那么他们之间的距离 就是 x2-x1+y2-y1=(x2+y2)- (x1+y1)
那么 我们不免发现 距离
要么 之和 x+y 有关 要么 只和 x-y 有关 那么答案就是
max{max{xi+yi}−min{xi+yi},max{xi−yi}−min{xi−yi}}
#include<bits/stdc++.h>
using namespace std;
int n,x,y;
template<typename T>inline void read(T &x)
{
x=0;T f=1,ch=getchar();
while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
while(isdigit(ch)) {x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
x*=f;
}
const int N=(1<<30);
int max1=-N,max2=-N,min1=N,min2=N;
int main() {
read(n);
for(int i=1;i<=n;i++) {
read(x); read(y);
max1=max(max1,x+y); min1=min(min1,x+y);
max2=max(max2,x-y); min2=min(min2,x-y);
}
cout<<max((max1-min1),(max2-min2));
return 0;
}
要理解一下这个转化
接下来 介绍一下切比雪夫距离
在二维空间内,两个点之间的切比雪夫距离为它们横坐标之差的绝对值与纵坐标之差的绝对值的最大值。
设点 A(x1,y1),B(x2,y2) ,则 A,B之间的切比雪夫距离用公式可以表示为:
$d(A,B) = \max(\left | x_1 - x_2\right | , \left | y_1 - y_2\right | )$
同样对于 n维的情况
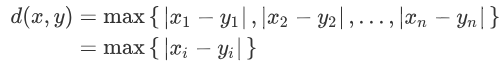
切比雪夫距离 的一般模型:
在国际象棋棋盘上,国王与王后从一个格子走到另一个格子的最短距离都是切比雪夫距离。
若网格图上的一个点只能到周围 8 个点,且到这 8 个点的距离都相同,则该网格图上两点的距离也为切比雪夫距离。
那么重点来了
我们现在要探讨二维曼哈顿距离与切比雪夫距离的相互转化
我这里简单证明一下吧

或者我还看过一个比较优秀的证明
假设 A(x1,y1),B(x2,y2) ,A,B 两点的曼哈顿距离为:

我们很容易发现,这就是 (x1+y1,x1−y1),(x2+y2,x2−y2) 两点之间的 切比雪夫距离。
所以将每一个点 (x,y)转化为 (x+y,x−y) ,新坐标系下的 切比雪夫距离 即为原坐标系下的 曼哈顿距离。
同理 A,B 两点的 切比雪夫距离 为:
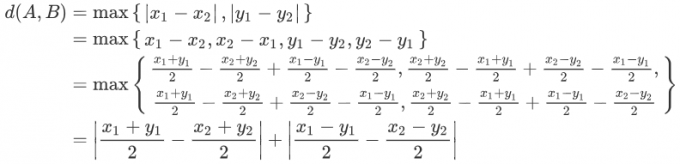
而这就是 $\displaystyle \left( \frac{x_1+y_1}{2},\frac{x_1-y_1}{2} \right),\left( \frac{x_2+y_2}{2},\frac{x_2-y_2}{2} \right)$ 两点之间的 曼哈顿距离。
所以将每一个点 (x,y) 转化为 $\displaystyle \left( \frac{x+y}{2},\frac{x-y}{2}\right)$ 新坐标系下的 曼哈顿距离 即为原坐标系下的 切比雪夫距离。
也就是 两个东西 可以相互转化 那么 对于有些题目 我们就要注意到 怎么计算简单了
在观察 上面那个问题 求曼哈顿距离 最大的点对 我们考虑转化成切比雪夫距离 那么 就是(x,y) 转化成 (x+y,x-y)
所求的答案就变为 max{max{∣xi−xj∣,∣yi−yj∣}}
在所有点中,横坐标之差的最大值和纵坐标之差的最大值都有可能成为答案,
所以我们只需要预处理出 x,y 的最大值和最小值即可。时间复杂度为 O(n) 。
例题下午会给出 因为 我现在眼睛太疼了。 不写了。