这一篇来讲讲线段树合并。
前置知识:动态开点线段树
还是一样先给一道例题:[JOI2012] Building2
题面是日文的,这里给出中文翻译:
有n个城市,它们组成了一棵树。 第i个城市有一座高度为Hi的建筑。
你需要选择一条尽量长路径,设路径中有k个点, 依次分别为i1,i2,⋯ik−1,ik,使得路径满足Hi1<Hi2<⋯<Hik,这k个点不一定要连续,求k的最大值。
概述:求树上LIS( 最长上升子序列 ),不会求LIS也没有关系,这只是一道例题。
先来考虑朴素做法:
取出树上的所有路径,对它们分别求LIS。
可以做,但是复杂度太高,不可行。
我们发散思维,容易想到一种做法:
对于每一个点x,我们发现经过它的一条路径的LIS可以由两部分组成。
以x开头,x左边的部分路径如果是下降的,那右边就要是上升的( 值h )。
以x开头,x左边如果是上升的,右边就要是下降的。
画个图方便理解:
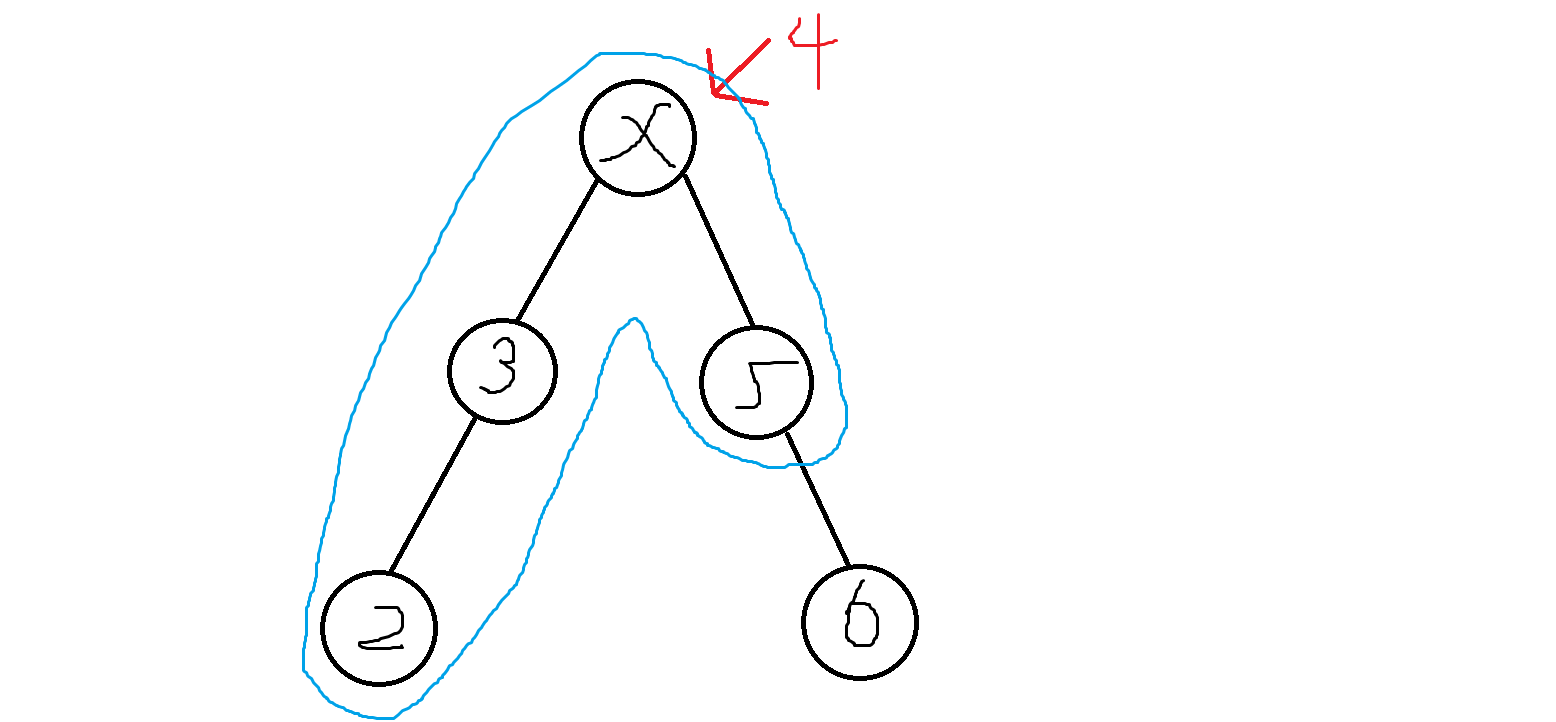
图中蓝色的显然就是过x的LIS
根据上面的想法,我们求出以x开头,往左的LIS=3,往右的LDS( 最长下降子序列 )=2。
以x开头,往左的LDS=1,往右的LIS=2。
我们比较两个结果( 相加-1,要把自己重复算的那一次减去 ),4和2,显然答案就是4。
现在考虑怎么实现这个想法,
刚开始,所有点的LIS和LDS都是1( 自己 )。
然后我们考虑从底向上合并答案。
dfs遍历到底,开始向上回溯,每次询问找到左右子树,直接合并答案。
如图:
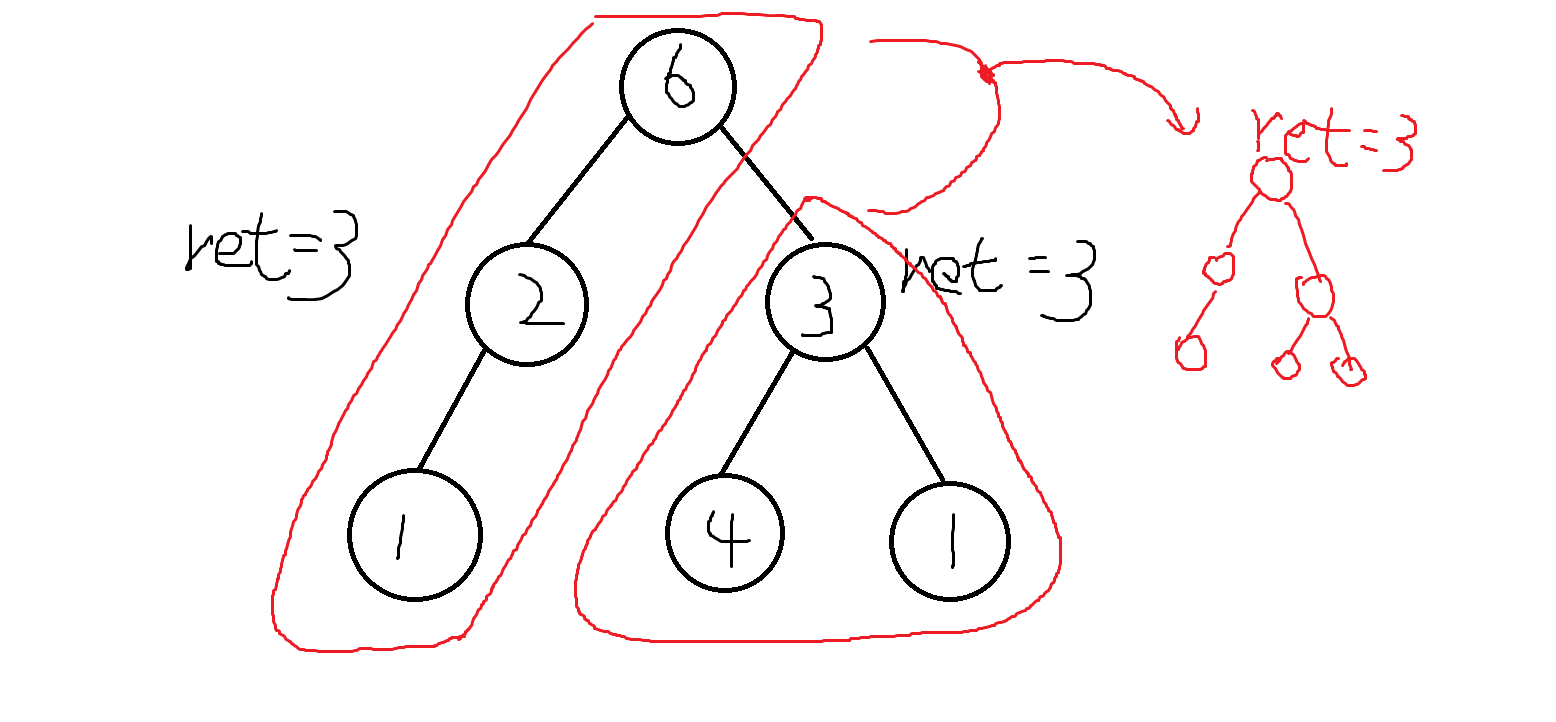
还是一样,理解一下就好。看不懂没关系,可以照着代码自己画几组数据看看合并过程。
我们用动态开点线段树维护一下这个合并,题就做出来了。
现在来讲线段树合并。
顾名思义,线段树合并就是把两棵线段树合并成一棵。
可以在合并的过程中更新信息。
线段树合并可以解决大部分更新答案需要合并的问题,dsu( 树上启发式合并 )能做的它也基本可以。
给出合并的代码,以上面的例题为例:
inline void Merge(int&x,int y){
if(!x||!y){
x=x+y;return;
}
lis[x]=_fmax(lis[x],lis[y]);
lds[x]=_fmax(lds[x],lds[y]);
ret=fmax(ret,_fmax(lis[lc[x]]+lds[rc[y]],lds[rc[x]]+lis[lc[y]]));
Merge(lc[x],lc[y]);
Merge(rc[x],rc[y]);
}
可以先学学可并堆(左偏树),线段树合并和可并堆是有挺多相似的地方的。
左偏树的博客在我写完线段树系列后大概会写一篇。毕竟日更博主...。
然后我们的其他操作就和动态开点线段树基本一致了。
但是节点值的更新,是每次修改都要更新,这一点不像动态开点线段树( 在叶子节点更新 )。
inline void Update(int&x,int l,int r,int pos,int val,int *h){
if(!x)x=++ncnt;
h[x]=_fmax(h[x],val);
if(l==r)return;
int mid=(l+r)>>1;
if(pos<=mid)Update(lc[x],l,mid,pos,val,h);
else Update(rc[x],mid+1,r,pos,val,h);
}
现在给出我写的上面那道例题的标程。
注释已经全部加好了,请放心食用。看不懂的地方可以在下方评论区里留言。
#include<bits/stdc++.h>
using namespace std;
#define getchar gc
char buf[1000010],*pos,*End;
inline char gc(){
if(pos==End){
End=(pos=buf)+fread(buf,1,1000000,stdin);
if(pos==End)return EOF;
}return *pos++;
}
//fread高速读入
const int N=100010;
struct Edge{
int u,v,nxt;
}e[N<<1];
int head[N],tot;
inline void addedge(int u,int v){
e[++tot].u=u;
e[tot].v=v;
e[tot].nxt=head[u];
head[u]=tot;
}//前向星存图
inline int _fmax(int x,int y){
return (((y-x)>>31)&(x^y))^y;
}//快速max
int ret;
int root[N];
int lc[N*20],rc[N*20],lis[N*20],lds[N*20],ncnt;//开nlogn个点
inline void Merge(int&x,int y){//合并
if(!x||!y){
x=x+y;return;
}
lis[x]=_fmax(lis[x],lis[y]);
lds[x]=_fmax(lds[x],lds[y]);//更新值
ret=_fmax(ret,_fmax(lis[lc[x]]+lds[rc[y]],lds[rc[x]]+lis[lc[y]]));
Merge(lc[x],lc[y]);
Merge(rc[x],rc[y]);//合并
}
inline void Update(int&x,int l,int r,int pos,int val,int *h){
if(!x)x=++ncnt;//开点
h[x]=_fmax(h[x],val);//每个节点都更新值
if(l==r)return;//到叶子节点就可以返回了
int mid=(l+r)>>1;
if(pos<=mid)Update(lc[x],l,mid,pos,val,h);
else Update(rc[x],mid+1,r,pos,val,h);//递归更新值
}
inline int Query(int&x,int l,int r,int L,int R,int *h){
if(l>r)return 0;
if(!x)return 0;
if(L<=l && r<=R)return h[x];//跟普通的动态开点线段树一样
int ret=0,mid=(l+r)>>1;
if(L<=mid)ret=_fmax(ret,Query(lc[x],l,mid,L,R,h));
if(R>mid)ret=_fmax(ret,Query(rc[x],mid+1,r,L,R,h));
return ret;
}
int d[N],kcnt;
inline int bis(int x){
return lower_bound(d+1,d+kcnt+1,x)-d;//离散化后查找值的二分
}
int n,val[N];
int ans;
inline void dfs(int x,int f){//dfs到底,回溯时进行合并
for(int i=head[x];i;i=e[i].nxt){
int y=e[i].v;
if(y==f)continue;
dfs(y,x);
}
ret=0;
int nlis=0,nlds=0,ilis,ilds;
for(int i=head[x];i;i=e[i].nxt){
int y=e[i].v;
if(y==f)continue;
ilis=Query(root[y],1,kcnt,1,val[x]-1,lis);//查找子树的lis
ilds=Query(root[y],1,kcnt,val[x]+1,kcnt,lds);//查找子树的lds
Merge(root[x],root[y]);//合并子树
ans=_fmax(ans,ilis+1+nlds);
ans=_fmax(ans,ilds+1+nlis);//更新答案
nlis=_fmax(nlis,ilis);
nlds=_fmax(nlds,ilds);//更新节点的值
}
ans=_fmax(ans,ret);//更新答案
Update(root[x],1,kcnt,val[x],nlis+1,lis);
Update(root[x],1,kcnt,val[x],nlds+1,lds);//更新线段树
}
inline int read(){
int data=0,w=1;char ch=0;
while(ch!='-' && (ch<'0'||ch>'9'))ch=getchar();
if(ch=='-')w=-1,ch=getchar();
while(ch>='0' && ch<='9')data=data*10+ch-'0',ch=getchar();
return data*w;
}
int main(){
n=read();
for(int i=1;i<=n;i++){
val[i]=read();
d[++kcnt]=val[i];
}
sort(d+1,d+kcnt+1);
kcnt=unique(d+1,d+kcnt+1)-d-1;//离散化
for(int i=1;i<=n;i++)
val[i]=bis(val[i]);
int x,y;
for(int i=1;i<n;i++){
x=read();y=read();
addedge(x,y);addedge(y,x);//加边
}
dfs(1,0);
printf("%d\n",ans);
return 0;
}
总结一下,遇到需要合并更新答案的题,就可以用线段树合并解决。
那么本篇到这里就结束了,撰文不易,希望帮到各位。
下一篇更新线段树优化建图,本系列持续更新,求点赞求关注。