一维搜索
一维最优化
一般迭代算法
- 初始点 \(x^0\)
- 按照某种规则 \(A\) 产生下一个迭代点 \(x^{k+1}=A(x^k)\)
- 点列 \({x^k}\) 收敛于最优解 \(x^*\)
下降迭代算法
- 初始点 \(x^0\)
- 按照某种规则 \(A\) 产生下一个迭代点 \(x^{k+1}=A(x^k)\)
- \(f(x^0)>f(x^1)>...>f(x^k)>...\)
下降迭代算法步骤:
给出初始点 \(x^0\),令 \(k=0\)
按照某种规则确定下降搜索方向 \(d^k\)
按照某种规则确定搜索步长 \(\lambda_k\),使得
\[ f\left(x^{k}+\lambda_{k} d^{k}\right)<f\left(x^{k}\right) \]令 \(x^{k+1}=x^{k}+\lambda_{k} d^{k}\)
判断 \(x^k\) 是否满足停止条件
搜索步长确定方法
\[ f\left(x^{k}+\lambda_{k} d^{k}\right)=\min _{\lambda} f\left(x^{k}+\lambda d^{k}\right) \]
称 \(\lambda_k\) 为最优步长,且有
\[
\nabla f\left(x^{k}+\lambda_{k} d^{k}\right)^{T} d^{k}=0
\]
收敛速度
设算法 \(A\) 所得的点列为 \(\{x^k\}\),如果
\[
\left\|x^{k+1}-x^{*}\right\|<\lambda\left\|x^{k}-x^{*}\right\|^{\alpha}, \quad \lambda, \alpha>0
\]
则称 \(\{x^k\}\) 的收敛阶为 \(\alpha\)
黄金分割法
思想:不断试探缩短包含极小点的区间,求得逼近的极小值。
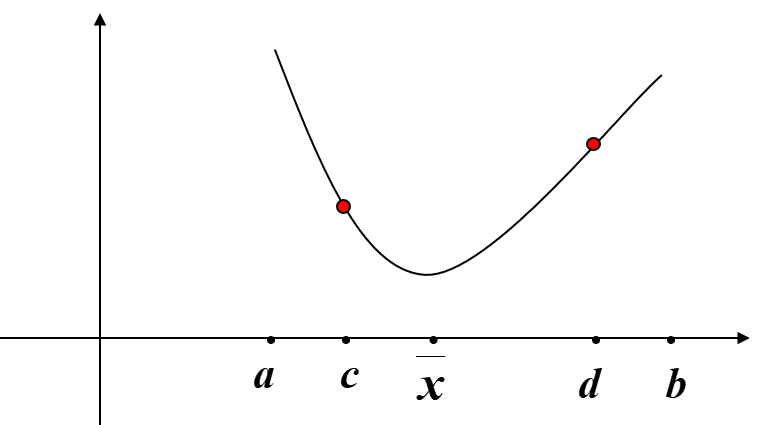
定理:设 \(f(x)\) 是区间 \([a,b]\) 上的一元函数,\(x'\) 是 \(f(x)\) 是区间 \([a,b]\) 上的极小点。任取点 \(c<d\in [a,b]\),则有
- 若 \(f(c)>f(d),x'\in[c,b]\)
- 若 \(f(c)<f(d),x'\in[a,d]\)
黄金分割法:设 \(f(x)\) 在 \([a_1,b_1]\) 上单峰,极小点 \(x'\in [a_1,b_1]\),假设进行第 \(k\) 次迭代前 \(x'\in [a_k,b_k]\),取 \(\lambda_k,\mu_k \in [a_k,b_k]\),且 \(\lambda_k<\mu_k\),则有
- 若 $f(\lambda_k)>f(\mu_k) $,令 \(a_{k+1}=\lambda_k,b_{k+1}=b_k\)
- 若 $f(\lambda_k)\le f(\mu_k) $,令 \(a_{k+1}=a_k,b_{k+1}=\mu_k\)
\(\lambda_k\) 与 \(\mu_k\) 需满足:
满足 \(b_k-\lambda_k=\mu_k-a_k\)
每次迭代区间长度缩短比率相同
\[ b_{k+1}-a_{k+1}=\alpha(b_k-a_k)\quad \alpha>0 \]
则
\[ \begin{cases}\lambda_k &=& a_k+(1-\alpha)(b_k-a_k)\\\mu_k &=& a_k+\alpha(b_k-a_k)\end{cases} \]第 \(k\) 次迭代时,假设 $f(\lambda_k)\le f(\mu_k) $,则区间更新为 \([a_{k+1},b_{k+1}]=[a_k,\mu_k]\),在第 \(k+1\) 次迭代时选取 \(\lambda_{k+1},\mu_{k+1}\),有
\[ \begin{array} \mu_{k+1}&=&a_{k+1}+\alpha(b_{k+1}-a_{k+1})\\&=& a_k+\alpha^2(b_k-a_k)\end{array} \]
令 \(\alpha^2=1-\alpha\Rightarrow \alpha=\frac{\sqrt{5}-1}{2}\approx 0.618\)同理可得,若 $f(\lambda_k)> f(\mu_k) $,区间更新为 $ [a_{k+1},b_{k+1}]=[\lambda_k,b_k] $,有
\[ \begin{array} \lambda_{k+1}&=&a_{k+1}+(1-\alpha)(b_{k+1}-a_{k+1})\\&=&a_{k+1}+0.382(b_{k+1}-a_{k+1})\end{array} \]
算法步骤:
给定初始区间 \([a_1,b_1]\),精读要求 \(\varepsilon>0\)。
令 \(\lambda_1=a_1+0.382(b_1-a_1)\),\(\mu_1=a_1+0.618(b_1-a_1)\),并计算 \(f(\lambda_1)\) 与 \(f(\mu_1)\)
若 \(b_k-a_k < \varepsilon\),算法结束。结果 \(x'=\frac{b_k-a_k}{2}\)。
否则,若 $f(\lambda_k)> f(\mu_k) $,转(3)。若 $f(\lambda_k)\le f(\mu_k) $,转(4)
区间更新为 $ [a_{k+1},b_{k+1}]=[\lambda_k,b_k] $,且 \(\lambda_{k+1}=\mu_k\) (减少计算,直接赋值),\(\mu_{k+1}=a_{k+1}+0.618(b_{k+1}-a_{k+1})\),计算 \(f(\mu_{k+1})\) ,\(f(\lambda_{k+1})\) 直接由 \(f(\mu_k)\) 得来,转(2)。
区间更新为 \([a_{k+1},b_{k+1}]=[a_k,\mu_k]\),且 \(\mu_{k+1}=\lambda_k\) ,\(\lambda_{k+1}=a_{k+1}+0.382(b_{k+1}-a_{k+1})\),计算 \(f( \lambda_{k+1})\) ,\(f( \mu_{k+1})\) 直接由 \(f(\lambda_k)\) 得来,转(2)。
进退法 ( 二次插值法 )
算法思路:利用目标函数在不同 3 点的函数值构成一个与原函数 \(f(x)\) 近似的二次多项式 \(p(x)\),以函数 \(p(x)\) 的极值点作为原函数 \(f(x)\) 的近似极值点。
计算步骤:
给定初始点 \(x_0\),初始步长 \(h_0\),计算 \(f(x_0)\),令 $k=0 $。
令 \(x_{k+1}=x_{k}+h_k\),计算 \(f(x_{k+1})\),若 \(f(x_{k+1})\le f(x_{k})\),转(3)。否则转(4)。
加大步长。令 \(h_{k+1}=2h_k\),\(x=x_k\),\(x_k=x_{k+1}\),令 \(k:=k+1\)。转(2)
反向搜索或输出。若 \(k=0\),令 \(h_1=h_0\),\(x=x_1\),\(x_1=x_0\),\(k=1\),转(2),否则停止迭代,令
\[ a=min\{x,x_{k+1}\},\quad b=max\{x,x_{k+1}\} \]
输出 \([a,b]\)。
抛物线插值法
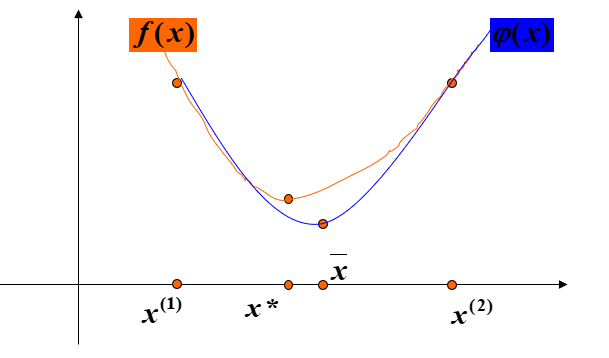
思想:在极小点附近,用二次三项式 \(\phi(x)\) 逼近目标函数 \(f(x)\),令 \(\phi(x)\) 与 \(f(x)\) 在三点 \(x_1<x_2<x_3\) 处有相同的函数值,并假设 \(f(x_1)>f(x_2)>f(x_3)\)。
设 \(\phi(x)=a+bx+cx^2\),代入 \(f(x_1)\) ,\(f(x_2)\), \(f(x_3)\) 三点值求解 \(\phi(x)\) 的系数,再求 \(\phi(x)\) 的极小值点 \(x'\) 作为 \(f(x)\) 极小点的估计值。
算法步骤:
- 给定区间 \([x_1,x_3]\),设 \(f(x_1)>f(x_2)\),\(f(x_2)>f(x_3)\),令 \(k:=1,x_0=x_1\)。给定精度 \(\varepsilon\)。
- 设 \(\phi(x)=a+bx+cx^2\)。令 \(\phi(x_i)=f(x_i),i=1,2,3\)。解出系数 \(a,b,c\)。解出 \(\phi(x)\) 的极小点 \(x'_k\)。若 \(|f(x'_k)-f(x'_{k-1})|<\varepsilon\),算法结束。否则转(3)。
- 从 \(x_1,x_2,x_3\) 和 \(x'_k\) 中选择 \(f(x)\) 的函数值最小的三个点重新标记为 \(x_1,x_2,x_3\),令 \(k:=k+1\),转(2)。
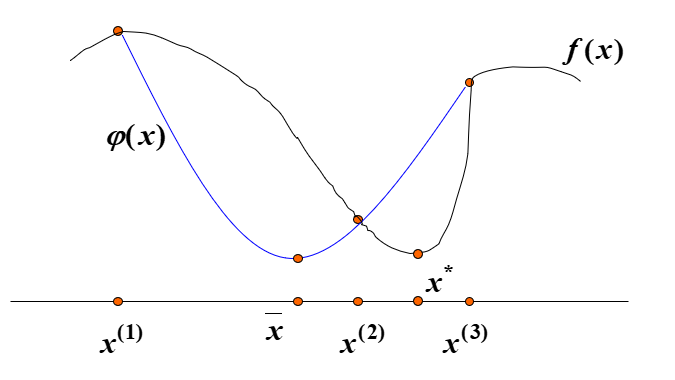
三次插值法
思路:已知\(f(x_1)、f(x_2),x_1<x_2\),且有 \(f'(x_1)<0\),\(f'(x_2)>0\),则区间 \((x_1,x_2)\) 内存在 \(f(x)\) 的极小点。利用 \(f(x_1)、f(x_2)、f'(x_1)、f'(x_2)\) 构造三次多项式 \(\phi(x)\),使得 \(\phi(x)\) 与 \(f(x)\) 在 \(x_1、x_2\) 有相同的函数值与导数。用 \(\phi(x)\) 逼近 \(f(x)\),并用 \(\phi(x)\) 极小点近似 \(f(x)\) 极小点。