So I got a 3d system and some coordinates:
- Start coordinates (x, y, z) of a rocket (on the ground)
- Target coordinates (x, y, z) of the rockets target (also on the ground)
I got some initialize values like:
- maximum_velocityZ = 0.5
- maximum_resVelocityXY = 0.3
- gravity factor = 9.81
How can I calculate the flight velocitys (velocityX, velocityY and velocityZ) for every update frame?
let maximum_velocityZ = 0.5
let maximum_resVelocityXY = 0.3
let gravity_factor = 9.81
let rocketPosition = {
x: 3,
y: 0,
z: 2
}
let rocketTarget = {
x: 7,
y: 5,
z: 8
}
let rocketVelocity = {
x: 0,
y: 0,
z: 0
}
let update = function() {
rocketPosition.x += rocketVelocity.x
rocketPosition.y += rocketVelocity.y
rocketPosition.z += rocketVelocity.z
let distanceX = (rocketTarget.x - rocketPosition.x)
let distanceY = (rocketTarget.y - rocketPosition.y)
let distanceZ = (rocketTarget.z - rocketPosition.z)
let factorXY = Math.abs(distanceX / distanceY)
rocketVelocity.x = maximum_resVelocityXY / Math.sqrt((1 / factorXY ** 2) + 1) * (distanceX > 0 ? 1 : -1)
rocketVelocity.y = maximum_resVelocityXY / Math.sqrt((factorXY ** 2) + 1) * (distanceY > 0 ? 1 : -1)
rocketVelocity.z = maximum_velocityZ * distanceZ;
rocketVelocity.z /= gravity_factor;
console.log("x:", Math.round(rocketPosition.x), "y:", Math.round(rocketPosition.y), "z:", Math.round(rocketPosition.z))
}
setInterval(update, 300)This code is what I've developed so far. I'm sure I'm on the right track. X and Y seem to be more or less right. Only the Velocity Z can't be calculated the way I tried. In 3D space the trajectory doesn't really look realistic. So by "not really" I mean "not realistic at all"...
I would be happy for help. Thanks and a happy new year - matching to the rocket - of course!
I do not know what is you coordinate system
- plane
- sphere
- ellipsoid like WGS84
My guess is your ground is planar (induced from your constants however your positions suggest something else)... so I will stick with that for now... You got 2 problems:
Newton/D'Alembert physics
Yours is weird as you got no
dtmultiplication so it works only if your update is 1 Hz. take a look at this:you do not need speed limiter as air friction will do it for you and you should drive with accelerations ... or Force if you want to account for mass changes too.
However as you are working with ground/ground then I assume atmospheric flight instead of Newtonian so in such case you need to handle the heading control not by acceleration but by turning the integrated velocity. The main thruster should still be handled as acceleration.
The collisions are not necessary in your case (unless your ground is not planar or have obstacles along the way).
Rocket guiding system
I suggest to use 3 state (Markovov model) rocket control.
launch
Rise the rocket to safe altitude first to avoid obstacles, conserve fuel and maximize speed
cruise
Travel to the target area (while still keep its altitude). Simply compute heading projected on the ground plane and apply correction to the heading of the rocket to match it (still going parallel to ground).
hit
Hit the target while descending. Almost the same as #2 but this time you need to change altitude too...
On top of these you can add strategies to avoid detection/destruction or obstacles etc ... You can also make a fake approach from different heading to keep the launch position hidden ...
Here a simple C++ example of this approach:
//---------------------------------------------------------------------------
void vector_one(double *c,double *a)
{
double l=sqrt((a[0]*a[0])+(a[1]*a[1])+(a[2]*a[2]));
if (l>1e-10) l=1.0/l; else l=0.0;
c[0]=a[0]*l;
c[1]=a[1]*l;
c[2]=a[2]*l;
}
//---------------------------------------------------------------------------
// Z=0 plane is ground, Z+ is up
const double g=9.81; // [m/s^2] Earth's gravity
const double acc0=20.0; // [m/s^2] rocket main thruster acceleration
const double kv2 =0.002; // [-] rocket air friction coeff (speed limiter)
const double alt0=50.0; // [m] rocket safe altitude
const double dis0=100.0; // [m] rocket safe distance to target
const double dis1= 10.0; // [m] rocket explosion distance to target
const double dang0=375.0*M_PI/180.0;// [rad/s] rocket turn speed per yaw/roll/pitch
// Rocket
double dst[3]={+90.0,-50.0,0.0}; // [m] target position
double pos[3]={-100.0,200.0,0.0}; // [m] rocket position
double vel[3]={ 0.0, 0.0,0.0}; // [m/s] rocket velocity
double acc[3]={ 0.0, 0.0,0.0}; // [m/s^2] rocket acceleration
enum{
_state_none=0,
_state_launch, // rise to alt0
_state_cruise, // get near target but maintain alt0
_state_hit, // descend and hit
};
int state=_state_launch;
void update(double dt) // update rocket after dt [sec] has passed
{
int i;
double v,a,hdg[3],tar[3];
// guiding system
if (state==_state_none)
{
for (i=0;i<3;i++) vel[i]=0.0;
for (i=0;i<3;i++) acc[i]=0.0;
return;
}
if (state==_state_launch)
{
// init heading to Up
for (i=0;i<3;i++) hdg[i]=0.0; hdg[2]=1.0;
if (pos[2]>=alt0) state=_state_cruise;
}
v=sqrt((vel[0]*vel[0])+(vel[1]*vel[1])+(vel[2]*vel[2]));// |vel|
if ((state==_state_cruise)||(state==_state_hit))
{
vector_one(hdg,vel); // heading
for (i=0;i<3;i++) tar[i]=dst[i]-pos[i]; // to target
a=sqrt((tar[0]*tar[0])+(tar[1]*tar[1])+(tar[2]*tar[2])); // distance to target
if (state==_state_cruise)
{
tar[2]=0; // no altitude change
if (a<=dis0) state=_state_hit;
}
else{
if (a<=dis1) state=_state_none; // here you shoul add exlosion code
}
vector_one(tar,tar);
// a = angle between hdg and tar [rad]
for (a=0.0,i=0;i<3;i++) a+=hdg[i]*tar[i];
a=fabs(acos(a));
// approximate turn up to dang0
if (a>1e-10) a=dt*dang0/a; else a=0.0;
for (i=0;i<3;i++) hdg[i]=hdg[i]+a*(tar[i]-hdg[i]);
vector_one(hdg,hdg); // new heading
for (i=0;i<3;i++) vel[i]=v*hdg[i]; // new vel
}
// physics
for (i=0;i<3;i++) acc[i] =-kv2*vel[i]*v; // air friction (k*|vel|^2)
for (i=0;i<3;i++) acc[i]+=hdg[i]*acc0; // rocket thrust
acc[2]-=g; // gravity
// Newton/D'Alembert simulation
for (i=0;i<3;i++) vel[i]+=acc[i]*dt;
for (i=0;i<3;i++) pos[i]+=vel[i]*dt;
}
//---------------------------------------------------------------------------
You might need to tweak the constants a bit to match your sizes and game needs. As you can see you can customize the rocket quite a lot which is ideal for game (tech upgrades).
The physics is straight forward Newton/D'Alembert (apart the vel turning due to wings) and the guiding system works as described above. In first state the rocket just rise to alt0 then it try to turn towards target with dang0 turn speed while maintaining altitude and when closer than dis0 it start also descending. If closer than dis1 the rocket should explode ...
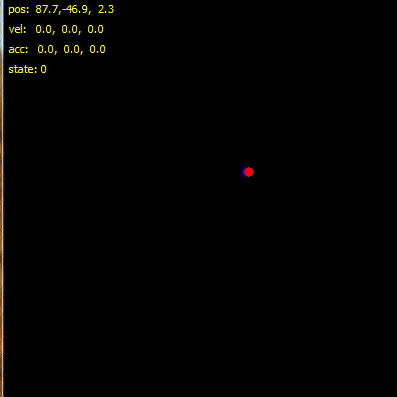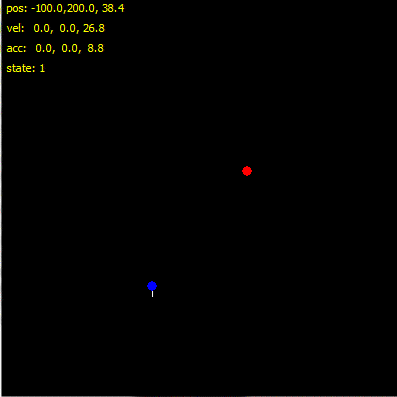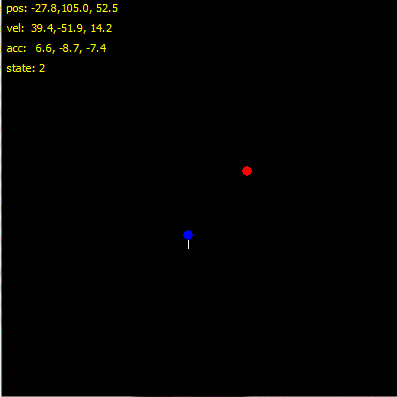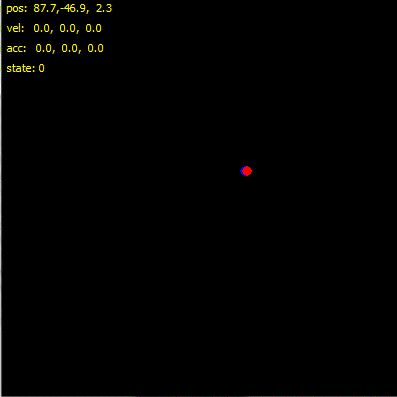
Here preview (top view):
The white line is line from ground to verify the altitude of rocket ... Rocket is Blue and target is Red.
The turning math is like this:
so I just scaled tar-hdg to approximately match dang0*dt and add that to original hdg. now the new heading is turned towards target by up to dang0*dt so just I normalize it back to unit size and recompute velocity to this new direction (as wings are turning velocity instead of accelerating)
Beware of the units
All the units used must be compatible I am using SI. Your 9.81 constant suggest the same but your position and target values makes no sense if in meters ... Why shoot rocket if target is just few meters away? Also the values suggest your coordinates are either not cartessian or ground is not planar/flat. Also the values suggest integers hope you have floats/doubles instead...
The trajectory will be a parabola. The basic equations of which are explained quite well here: https://courses.lumenlearning.com/boundless-physics/chapter/projectile-motion/
The 3D problem (x, y, z) can be easily be transformed to a 2D (single plane) problem (horizontal, vertical), for the equations then back to 3D for the problem.
来源:https://stackoverflow.com/questions/53978393/how-to-calculate-rocket