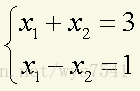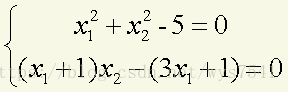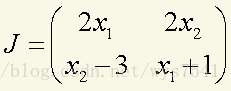1、R语言矩阵函数
2、求解线性方程组
分析:使用函数solve(a,b),运算a%*%x=b得到x。 a<-matrix(c(1,1,1,-1),2,2); b<-c(3,1); solve(a,b) 运行结果 > a<-matrix(c(1,1,1,-1),2,2);b<-c(3,1);solve(a,b) [1] 2 1 注:这里矩阵a从数组读数是按照列读数
解:先求Jacob行列式(求偏导)
相应的程序(程序名为:Newtons.R)为 Newtons<-function(fun,x,ep=1e-5,it_max=100){ index<-0;k<-1; while(k<it_max){ x1<-x;obj<-fun(x);x<-x-solve(obj$J,obj$f);norm<-sqrt((x-x1)%*%(x-x1)); if(norm<ep){index<-1;break}; k<-k+1} obj<-fun(x); list(root=x,it=k,index=index,FunVal=obj$f) } 在这个函数中,输入变量有:fun是方程构成的函数,x是初始变量,ep是精度要求,缺省时为e-5,it_max是最大迭代次数,缺省为100. 输出变量有:root是方程解的近似值,it是迭代次数,index是指标,index=1表明计算成功,index=0表明计算失败。FunVal是方程在 root处的函数值。编写求方程的程序(程序名为:funs.R)为 funs<-function(x){ f<-c(x[1]^2+ x[2]^2-5, (x[1]+1)*x[2]-(3*x[1]+1)) J<-matrix(c(2*x[1], 2*x[2],x[2]-3, x[1]+1),nrow=2,byrow=T) list(f=f,J=J) } 在这个函数中,输入变量是x,函数内部,f表示所有方程左边的函数,J是相应的Jacob矩阵. 输出变量有:函数值和相应的Jacob矩阵。 下面求解方程。 >Newtons(funs,c(0,1)) $root [1] 1 2 $it [1] 6 $index [1] 1 $FunVal [1] 1.598721e-14 6.217249e-15 即方程的解x*=(1,2)T,总共迭代了6次。 4、一元函数求极值

文章来源: R语言解线性方程组和求极值