前言
模拟退火算法(SA)是较为常见的现代优化算法之一,常用于旅行商(TSP)问题中。数学建模里学生们常常使用该算法,甚至是为了使用这个算法而使用这个算法,让评委老师们审美疲劳。评委老师明确表明使用所谓"神算法"(神经网络,模拟退火,遗传算法等等)而过于牵强者拿不了高分(见:http://special.univs.cn/service/jianmo/sxjmyw/2018/1128/1187951_15.shtml)。希望大家不要觉得它名词高级就认为它能吸引评委眼睛,评委毕竟是教授,不可能被几个名词唬住。
但是呢,我们是学生,不能因为它不能随便用就不学习它,而在编程的环节中,我们亦有收获,况且爱因斯坦也是从一加一开始学起的,所以模拟退火算法还是有学习的必要的。话说的有点多,下面进入主题。
算法框架
模拟退火算法可以粗分为以下几个步骤:
1,初始温度的设置、初始解的生成、设置每个温度下产生解的个数。
2,产生新解。
3,计算代价函数差。
4,Metropolis判别。(别被名词吓住,形式上是很简单的一个原则)
5,降温。
6,判断温度是否小于一个给定量。是,则结束;否,则跳转到第2步。
以下对每个步骤做详细的解释。
初始温度的设置、初始解的生成、设置每个温度下产生解的个数:
初始温度与降温系数、终止温度息息相关,它们仨决定了迭代的次数,具体公式为:终止温度 ≈ 初始温度*(降温系数)^迭代次数,其中1降温系数是(0,1)的一个常数 。对于小规模的问题,一般初始温度取1000,终止温度取1e-4,降温系数取0.9。这些参数直接影响了Metropolis判别。
初始解的生成一般是随机生成,因为SA算法对初始解的依赖并不大。
设置每个温度下产生解的个数的目的是增加样本量,增强算法的健壮性。多组解称为Metropolis的链长。
产生新解
产生新解的方式有很多种,最简单的是随机产生新解,当然也可以按照一定的算法产生新解。随机产生新解的好处是容易寻找到全局最优点,按一定算法产生新解的好处是在知道解大致位置的前提下可以更好的收敛。
计算代价函数差
计算代价函数差,即将最新解、最优解做差,得到增量df。
Metropolis判别
该判别的公式如下:
意义为,当代价函数差小于0(即新解比最优解的值还要小),接受最新解变为最优解;当代价函数不小于0时,以一定概率P接受该解作为最优解。由此可以看到,温度越高,劣解接受率也越低,换言之就是全局搜索能力更强。所以设置初始温度时,要将温度设置的比较高,避免陷入局部最优。
降温
降温方式较为简单,即新温度=当前温度*降温系数。从中可以看到迭代次数与初始温度、降温系数都有关系,但注意,初始温度影响了Metropolis判别,所以若要想提高迭代次数,提高降温系数较为合适。最后就是判断当前温度是否小于终止温度。以上就是关于模拟退火算法流程的个人理解,接下来将设计程序,以解决TSP问题。
程序设计
%模拟退火算法 %TSP问题 clc,clear T0 =500;%初始温度 Tend = 1e-4; %终止温度 L=200; %各个温度下的链长 q=0.98; %降温速率 cityNum = 30; %城市个数 City = rand(cityNum,2); %随机生成城市的坐标 %%%%%%%%%%%%%%主程序%%%%%%%%%%%%%%%%%%%% D = Distance(City); N = cityNum; S1 = randperm(N); %产生一个随机解 %解方程,计算迭代次数 Time = ceil(double(solve(['1000*(0.9)^x',num2str(Tend)]))); count = 0; %迭代计数器 Obj = zeros(Time,1); %每代路径和 track = zeros(Time,N); %每代最优解 %迭代 while T0>Tend count = count + 1; temp = zeros(L,N+1); for k = 1:L %产生L组新解 S2 = newSolution(S1); [S1,R] = Metropolis(S1,S2,D,T0); temp(k,:)=[S1 R]; end %记录每次迭代过程的最优路线 [d0,index] = min(temp(:,end)); if count == 1 || d0 <Obj(count-1) Obj(count) = d0; else Obj(count)=Obj(count - 1); end track(count,:)=temp(index,1:end-1); T0 = q*T0; end fprintf('迭代次数:%d\n',count); fprintf('最短路径:%f\n',Obj(end)); %迭代图 figure plot(1:count,Obj); xlabel('迭代次数'); ylabel('距离'); title('优化过程'); DrawPath(track(end,:),City); %%%%%%%%%%%%%%%%%子函数,共5个%%%%%%%%%%%%%%%%%%%%% %函数功能:求解距离矩阵 %输入:城市坐标 输出:距离矩阵 function D = Distance(a) r = size(a,1); D = zeros(r,r); for i = 1:r for j = i+1:r D(i,j)=sqrt((a(i,1)-a(j,1))^2 + (a(i,2)-a(j,2))^2); D(j,i) = D(i,j); end end end %函数功能:生成新解 %输入:旧解 输出:新解 %随机选两个位置交换。 function S2 = newSolution(S1) N = length(S1); S2 = S1; a = round( rand(1,2)*(N-1)+1); %产生两个随机位置用来交换 temp = S2(a(1)); S2(a(1))=S2(a(2)); S2(a(2)) = temp; end %Metropolis准则函数 %输入:新解,旧解,距离矩阵,当前温度 %输出:判断后的解,解的路径 function [S,R] = Metropolis(S1,S2,D,T) R1 = pathLength(D,S1); R2 = pathLength(D,S2); dT = R2 - R1; if dT < 0 S=S2; R=R2; elseif exp(-dT/T) >= rand S=S2; R=R2; else S=S1; R=R1; end end %画出路线轨迹图 %输入:最优路径,城市坐标 输出:路径图 function DrawPath(BestTrack,City) N = size(BestTrack,2); cityArray = zeros(N,2); for i = 1:N cityArray(i,1) = City(BestTrack(i),1); cityArray(i,2) = City(BestTrack(i),2); end figure; hold on plot(cityArray(:,1),cityArray(:,2),'-o','color',[0.5 0.5 0.5]); plot([cityArray(1,1),cityArray(end,1)],[cityArray(1,2),cityArray(end,2)],... '-','color',[0.5 0.5 0.5]); hold off xlabel('横坐标'); ylabel('纵坐标'); title('TSPͼ'); box on end %计算路线长度的函数 %输入:距离矩阵,行走的顺序 输出:路径和 function len = pathLength(D,S) [r,c] = size(D); NIND = size(S,1); for i = 1:NIND p = [S(i,:) S(i,1)]; i1 = p(1:end-1); i2 = p(2:end); len(i,1) = sum(D((i1-1)*c + i2)); end end
注意子函数newSolution,我的策略是随机挑选两个位置进行交换。事实上还可以采用其他策略来产生新解,但我太懒了,所以没想更好的产生新解的方法。
程序结果

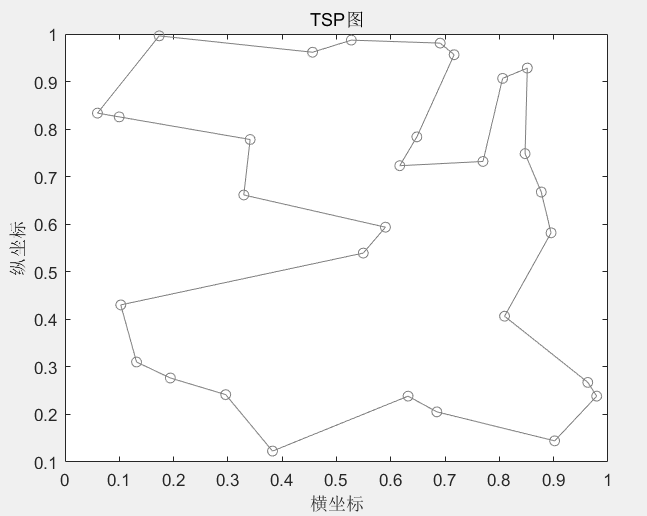
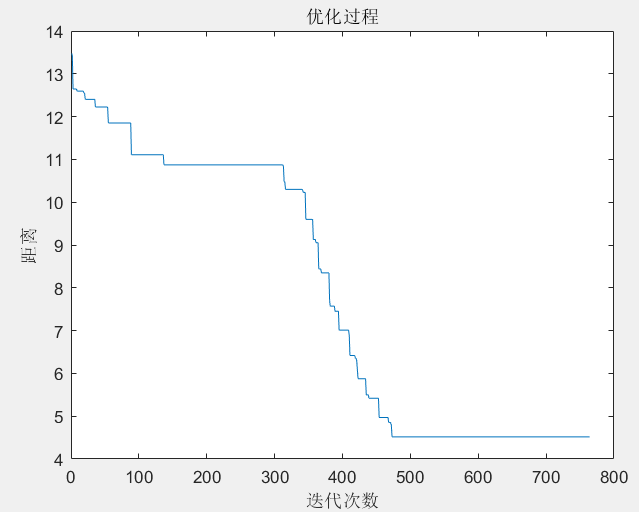
最后,我测试了一下当城市数为50,需要增大迭代次数,增大初始温度才能得到较好的解。当然,我产生新解的方式也较为简单,也可以从这方面考虑,用更好的想法来产生新解。
参考文献
[1] 郁磊,史峰,王辉等,《matlab智能算法30个案例分析(第二版)》,2015.8.
来源:博客园
作者:文野后生
链接:https://www.cnblogs.com/wenyehousheng/p/11486598.html