写给小陈~
参考文献:
Chou X., Gambardella L.M., Montemanni R. (2018) Monte Carlo Sampling for the Probabilistic Orienteering Problem. In: Daniele P., Scrimali L. (eds) New Trends in Emerging Complex Real Life Problems. AIRO Springer Series, vol 1. Springer
I. 什么是概率路线规划问题?
假设你是个推销员,任务是在有限时间内拜访一大堆的客户。每个客户在时限前成功拜访都有不同的收益,但是客户都挺忙的有一定概率不在,而且你的时间也不够拜访所有客户。那么问题来了:如何规划一条最短且收益期望最高的路线?

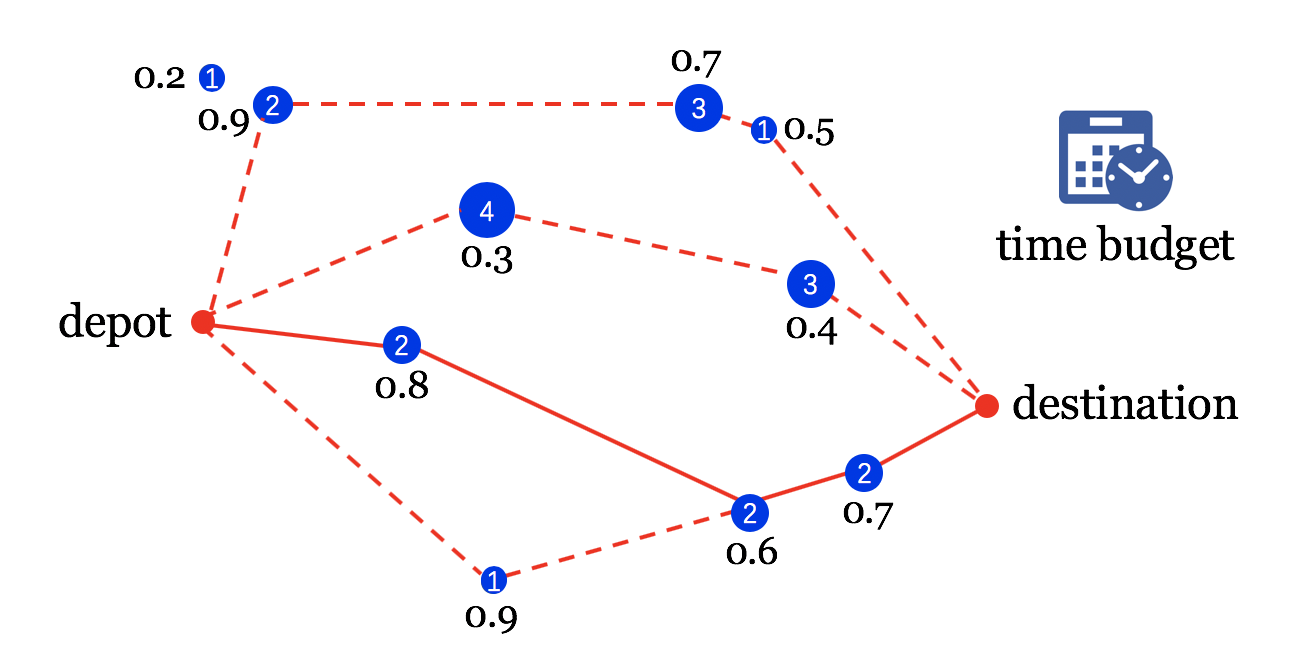
注:每个蓝色的点代表一个客户的实际地理位置,圆圈内数字是收益奖励,红色的点则是固定的起点和终点,无奖励
首先我们需要把问题建成一个数学模型。这里的变量和约束条件都是很明确的,难点在于目标函数:如何表达旅行距离的期望值和获得收益的期望值。
假设我们用旅行时间来表示两点之间的距离,根据每个点的概率排列组合出所有路线组合,还是可以写出一个旅行时间的期望值公式的。那么收益的期望值呢?
对于任意一个蓝点来说,这个客户的奖励拿不拿的到取决于两点:1. 到达时间有没有超过时限 2.客户在不在。
对于条件1来说,在不同的路线走法中,同一个点的到达时间是不一样的,所以并没有一个简单的公式来表达这个收益的期望值。而条件2也会导致路线决策的变化:
例:在下面四条可能的路线中,第二条路线的收益最高。然而这两位都是大概率不在的客户,那么就收益的期望值来说,第三条路线似乎更高。

综上,这个问题并不能简单的写成一个数学模型然后直接丢进cplex,gurobi等牛逼的求解器里去解。这种情况下,蒙特卡洛算法似乎是个不错的选择。
III. 如何用蒙特卡洛算法解决?
简单来说,只要对于一个路线我们有办法算出它目标函数的期望值,那么接下来就可以通过各种局部搜索算法(启发式算法或精确算法)去对比各种可能存在的路线的目标函数值,最终决策出满足目标函数的最优路线。而蒙特卡洛在表达这个目标函数的期望值这一点上很有优势。
具体来说,根据每个客户在的概率,我们随机取样。在任何一个样本中,客户在或不在是确定的事情。不在的客户可以直接跳过去下一个在的客户。这样一来,在任何一个样本中这条路线的总时间和总收益是一个确定值,则目标函数也有一个确定值。所有样本的目标函数的平均值就是目标函数的期望值。只要样本的数量足够大,蒙特卡洛取样法就可以跳过复杂的概率公式直接得到目标函数的期望值。
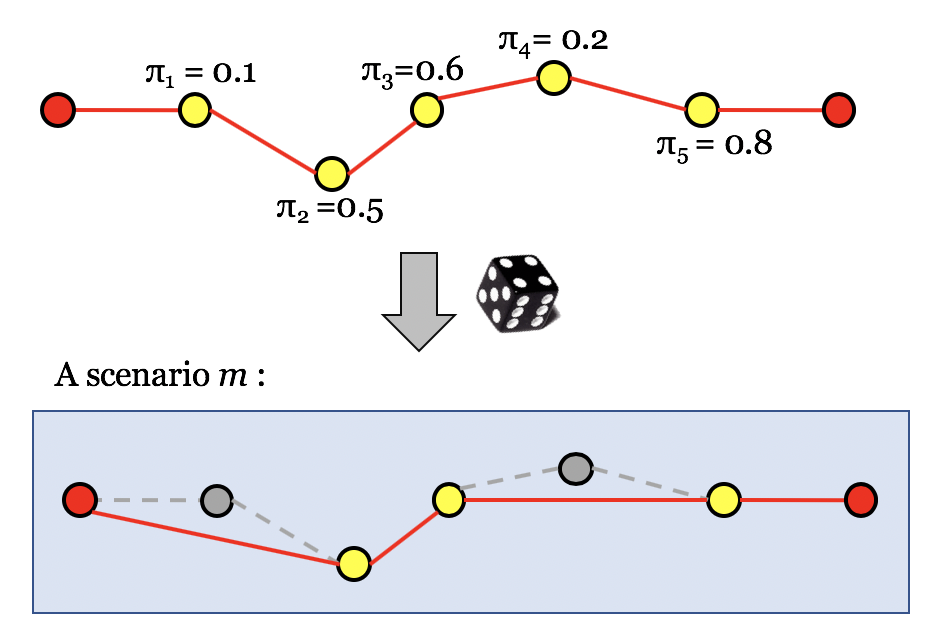
蒙特卡洛取样在实际操作中非常之快,尤其对于客户数量极大的问题。而样本数的抉择,是需要调试来找到最适合这个问题的样本数。参考文献中有对于该问题的具体实验数据,及用于改良提速的启发式算法思路。