学习策略:间隔最大化(解凸二次规划的问题)
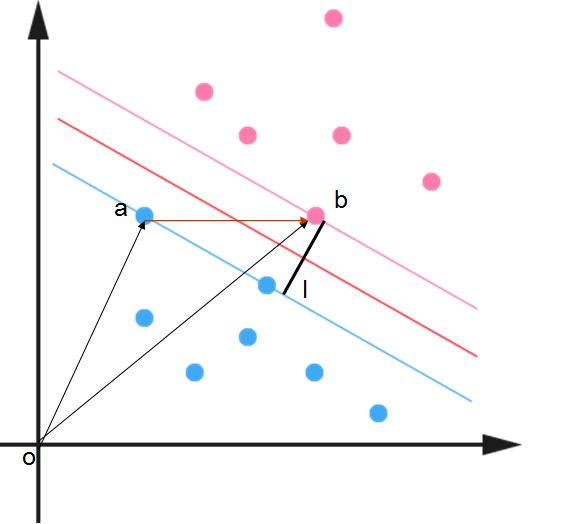
对于上图,如果采用感知机,可以找到无数条分界线区分正负类,SVM目的就是找到一个margin 最大的 classifier,因此这个分界线(超平面)一定是固定。
假设a是正类,b是负类,那么a和b直接的距离就是ob-oa在直线l上的映射。
我们假设a,b所在的那条直线的方程为:
a: WTX+b=1 b: WTX+b=1
那么根据两条平行线之间的距离公式,我们可以算出,平行线之间的间隔为:2/||w||。那么SVM便可以变为求解约束的最优化问题,如下:
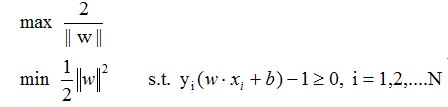
对于这种约束问题,作为一个凸优化问题(二次优化问题,目标函数时二次的,约束条件是线性的),我们可以使用现成的QP优化包进行求解。但是呢,由于这个优化问题的特殊结构,我们可以通过
Lagrange Duality 变换到对偶变量 (dual variable) 的优化问题,这样就可以更加方便进行求解了。
原始问题为求解如下的优化问题:
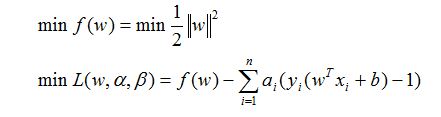
假设y(wx+b)-1!=0,那么我们可以通过调节相应的a使得L趋于负无穷。显然这不是我们要的情况,因此我们定义如下一个函数:

我们可以观察到当a>=0时,该函数等于L。因此求解问题可以写成如下形式:
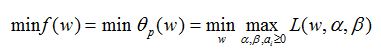
一般来说:
但是假设满足传说中的KTT条件,那么:
正好,我们的问题符合这个条件(这边不做说明)。这时候我们就可以固定ª,ß对w,b进行求偏导(注意原始形式是不可以这么直接求偏倒的,但是通过这么转换便可以了)
将求出的代入到L函数,
最后我们的原始问题变转化成求解如下问题:
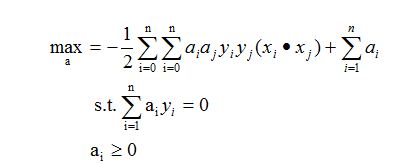
这时候通过求解这些a就可以了,可以使用SMO算法。
SMO:是SVM的一个实现方法,用到坐标递增法,就是固定两个参数。就是不断地将原二次规划问题分解为只有两个变量的二次规划子问题。
线性分类器也叫感知机,就是在N维的数据空间找到一个分类超平面。然后svm其实就是寻找间隔最大化的线性分类器。
首先说他在线性可分的数据集上的:
超平面就是在n维空间上可以将数据线性分类的平面。
超平面: WTX+b=0 W为向量,b是截距 ,这样就通过寻找最大间隔,确定W和b。把求f(x)=WTX+b转化为求w与b的最优化问题。
函数间隔:人为定义的,就是yf(x)
几何间隔:点到超平面的距离,f(x)/||w||
由于我们可以通过缩放w的倍数,设置函数间隔为1,这样就变成求max 1/||w||,也就是求min 1/2w2问题当然还有约束条件st。变成就凸二元问题。
还有可以通过对偶方法求解。
但是由于数据有时候不能够线性可分,但是通过将他们映射到高维空间,就可以线性可分。所以这样svm就可以处理线性不可分的问题。但是由于维数的增加,这样会导致“维数灾难”,
导致计算复杂,这时候就可以使用核函数,核函数就我目前理解就是通过使用它可以在数据原来的维度上计算内积,之后在分类,而不用计算高维。具体原理,看不懂。
核函数有好几个以及对应的参数,这个上网查吧。
最近又琢磨了一下:
核函数:就是当我们数据是线性可分的时候,求出来的决策函数是一个关于实例之间的内积<X1,X2>,那么当我们数据不可分的时候,就想把X映射到高维去f(x),这样可能就可以
线性可分了,然后决策函数就是<f(x1),f(x2)>,按道理我们是应该把点映射到高维之后,再去求内积,但是有时候映射的维数很大,很多情况下还是无限维的,所以计算量太大。
这时候我们就应该采用核函数。我们不用显示的去构造说明原来的点如何映射到高维的函数,就是不用去定义f(x),反正就是不用去想着把点如何去映射到高维。只要找到一个核函数
就可以,让核函数自己去映射,我们只要计算核函数就ok了。
常用核函数:
1)多项式核函数K(x,z)=(x*z+1)p,对应的支持向量机是一个p多项式分类器。
2)高斯核函数(有参数)
3)字符串核函数
对于参数的选择,一般都是拿出1/3用来选择最优参数。就有点自动参数优化的样子,比如像weka里的cvparamter一样。
还有就是当有时候数据是近线性可分的时候,有一些点可能会在不对劲的地方,就是没在他应该在的地方,这时候我们引入松弛变量和惩罚因子。
smo:是svm的一个实现方法,用到坐标递增法,就是固定两个参数。就是不断地将原二次规划问题分解为只有两个变量的二次规划子问题。