莫比乌斯反演
莫比乌斯函数
\(\mu(n)=1,n=1\)
\(\mu (n)=(-1)^m, n=\prod^m_{i=1}p_i^{k_i},\forall k_i = 1\)
\(\mu (n)=0 ,otherwise\)
性质
- 积性函数
- \(\sum _{i|n} \mu(i)=\epsilon (\epsilon = [n=1])\)
筛法
inline void init(){
mu[1]=1;
for(int i=2;i<=n;i++){
if(!np[i]) pri[++top]=i;
for(int j=1;j<=top&&i*pri[j]<n;j++){
int now=i*pri[j];
np[now]=1;
if(i%pri[j]) mu[now]=-mu[i];
else{
mu[now]=0;break; //出现平方因子
}
}
}
}
狄利克雷卷积
\((f∗g)(n)=∑_{d|n}f(d)∗g(\frac{n}{d})\)
数论函数与狄利克雷卷积形成群,满足结合律,封闭性,单位元,逆元,同时还满足交换律
其中单位元为\(ϵ\),\(ϵ(n)=[n=1]\)
比较常用的积性数论函数备用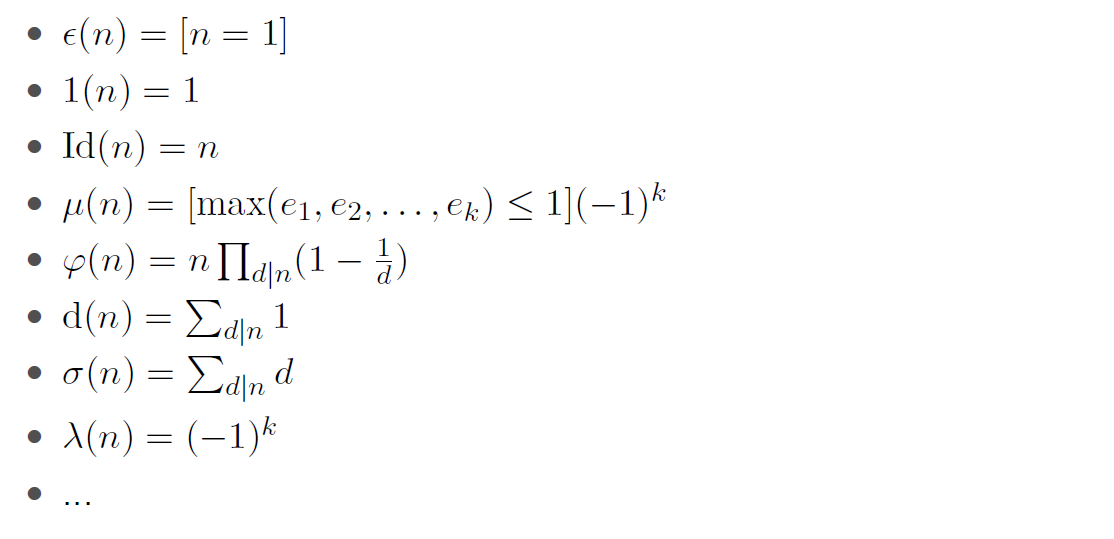
反演
有\(f(n)=\sum_{i|n}g(i)\)
结论:\(g(n)=\sum_{d|n}f(\frac{n}{d})*{\mu(d)}=\sum_{d|n}f(d)\mu(\frac{n}{d})\)
证明
展开f:
\[
g(n)=\sum_{d|n}\sum_{i|\frac{n}{d}}g(i)*\mu(d)
\]
提\(\mu\)到前面
\[
g(n)=\sum_{d|n}\mu(d)*\sum_{i|\frac{n}{d}}g(i)
\]
换\(\sum\),注意取值范围
\[
g(n)=\sum_{i|n}g(i)*\sum_{d|\frac{n}{i}}\mu(d)
\]
考虑后面\(\sum_{d|\frac{n}{i}}\mu(d)\)
- \(i=n,d=1\) ,此时\(\mu(d)=\mu(1)=1\),\(g(i)*\sum_{d|\frac{n}{i}}\mu(d)=g(n)\)
- \(i<n,\frac{n}{i}!=1\),此时\(\sum_{d|\frac{n}{i}}\mu(d)=\epsilon(\frac{n}{i})=0\),乘上 \(g(i)\) 还是 \(0\)
于是两种情况相加就是 \(g(n)\),原等式成立
用狄利克雷卷积写起来就是\(f=g*1 , g=f*\mu\)
第二种形式
\[ f(d)=\sum_{i=1}^{\lfloor\frac{n}{d}\rfloor}g(i\times d) \]
\[ g(d)=\sum_{i=1}^{\lfloor\frac{n}{d}\rfloor}f(i\times d)\mu(i) \]
应用
二维gcd数数
对于给定的整数\(a,b\)和\(d\),有多少正整数对 \(x,y\),满足 \(x\leq n\),\(y\leq m\),并且 \(gcd(x,y)=d\)
要求的数:
\[
\sum_{i=1}^{n}\sum_{j=1}^m [gcd(i,j)==d]
\]
转换一下:
\[
=\sum_{i=1}^{n}\sum_{j=1}^m \epsilon(gcd(\frac{i}{d},\frac{j}{d}))
\]
\[ =\sum_{i=1}^{\frac{n}{d}}\sum_{j=1}^{\frac{m}{d}} \epsilon(gcd(i,j)) \]
法一
利用莫比乌斯函数的性质:
\[
=\sum_{i=1}^{\frac{n}{d}}\sum_{j=1}^{\frac{m}{d}}\sum_{g|gcd(i,j)}\mu(g)
\]
\[ =\sum_{i=1}^{\frac{n}{d}}\sum_{j=1}^{\frac{m}{d}}\sum_{g|i且g|j}\mu(g) \]
考虑枚举\(g\),设\(N = \frac{n}{d},M = \frac{m}{d}\)
归类得:
\[
\sum_{g=1}^{N}\sum_{i=1}^{\lfloor\frac{N}{g}\rfloor}\sum_{j=1}^{\lfloor\frac{M}{g}\rfloor}\mu(g)
\]
\[ \sum_{g=1}^{N}\mu(g)\sum_{i=1}^{\lfloor\frac{N}{g}\rfloor}\sum_{j=1}^{\lfloor\frac{M}{g}\rfloor} \]
然后后面那个东西的共同取值一种只有\(\sqrt{n}+\sqrt{m}\)种,数论分块求得
法二
还是令
\[
f(d)=\sum_{i=1}^{n}\sum_{j=1}^m [gcd(i,j)==d]
\]
\[ g(d)=\sum_{i=1}^{n}\sum_{j=1}^m [d|gcd(i,j)] \]
\(f(k)\)为答案,\(g(k)\)明显等于\(\lfloor\frac{n}{k}\rfloor\lfloor\frac{m}{k}\rfloor\)
根据定义,
\[
g(d)=\sum_{i=1}^{\lfloor\frac{n}{d}\rfloor}f(i\times d)
\]
反演得
\[
f(d)=\sum_{i=1}^{\lfloor\frac{n}{d}\rfloor}g(i\times d)*\mu(i)
\]
套用\(g\),令设\(N = \frac{n}{d},M = \frac{m}{d}\)
\[
f(d)=\sum_{i=1}^{\lfloor\frac{n}{d}\rfloor}\lfloor\frac{N}{i}\rfloor\lfloor\frac{M}{i}\rfloor\mu(i)
\]
然后数论分块
数论分块的tips
对于有两个整除的,我们知道复杂度是\(\sqrt{n}+\sqrt m\)
单个数论分块的实现方法:
假设当前区间开头是\(i\),并且下一个区间是\(j+1\)
有
\[
\lfloor\frac{N}{i}\rfloor \leq \lfloor\frac{N}{j}\rfloor
\]
\[ \lfloor\frac{N}{i}\rfloor \leq \frac{N}{j} \]
\[ j\leq \frac{N}{\lfloor \frac{N}{i}\rfloor} \]
\[ j\leq \lfloor \frac{N}{\lfloor \frac{N}{i}\rfloor}\rfloor \]
两个数的同理,取min就好了
代码:
for(int l=1,r;l<=n;l=r+1){
r=min(n/(n/l),m/(m/l));
...
}
题解代码:
#include<iostream>
#include<algorithm>
#include<iostream>
#include<cmath>
#include<cstdio>
#define ll long long
using namespace std;
const int N = 50021;
inline int read(){
int x=0,pos=1;char ch=getchar();
for(;!isdigit(ch);ch=getchar()) if(ch=='-') pos=0;
for(;isdigit(ch);ch=getchar()) x=(x<<1)+(x<<3)+ch-'0';
return pos?x:-x;
}
int np[N],pri[N],top,mu[N],tomu[N];
void init(){
mu[1]=1;
for(int i=2;i<N;i++){
if(!np[i]){
pri[++top]=i;
mu[i]=-1;
}
for(int j=1;j<=top&&i*pri[j]<N;j++){
int now=i*pri[j];np[now]=1;
if(i%pri[j]==0){
mu[now]=0;break;
}else{
mu[now]=mu[i]*-1;
}
}
}
for(int i=1;i<N;i++){
tomu[i]=tomu[i-1]+mu[i];
}
}
int T;
int main(){
init();
T=read();
while(T--){
int a=read(),b=read(),d=read();
int n=a/d,m=b/d;
if(n<m) swap(n,m);
int ans=0;
for(int l=1,r;l<=n;l=r+1){
if(n/l==0||m/l==0){
r=n;
}else r=min((n/(n/l)),(m/(m/l)));
ans+=(n/l)*(m/l)*(tomu[r]-tomu[l-1]);
}
printf("%d\n",ans);
}
return 0;
}
练习题目
YY的gcd
gcd(x,y)为质数的区间数点
\[
\sum_{i=1}^{n}\sum_{j=1}^{m}[gcd(i,j)为质数]
\]
\[ =\sum_{d\in prime}\sum_{i=1}^{n}\sum_{j=1}^{m}[gcd(i,j)=d] \]
令
\[
f(d)=\sum_{i=1}^{n}\sum_{j=1}^{m}[gcd(i,j)=d]
\]
\[ g(d)=\sum_{i=1}^{n}\sum_{j=1}^{m}[d|gcd(i,j)] \]
然后
\[
g(d)=\sum_{i=1}^{\lfloor\frac{n}{d}\rfloor}f(i\times d)
\]
求的就是
\[
\sum_{d\in prime}\sum_{i=1}^{\lfloor\frac{n}{d}\rfloor}g(i\times d)*\mu(i)
\]
令 \(k =i\times d\)
\[
\sum_{d \in \text { prime }} \sum_{i=1}^{\left\lfloor\frac{n}{d}\right\rfloor} \mu(\frac{k}{d})\left\lfloor\frac{n}{k}\right\rfloor\left\lfloor\frac{m}{k}\right\rfloor
\]
枚举\(k\),
\[
\sum_{k=1}^{n}\lfloor\frac{n}{k}\rfloor\lfloor\frac{m}{k}\rfloor\sum_{d\in \text{prime},d|k}\mu(\frac{k}{d})
\]
令
\[
f(k)=\sum_{d\in \text{prime},d|k}\mu(\frac{k}{d})
\]
考虑线性筛\(f\)
k为质数,\(f(k)=\mu(\frac{k}{k})=\mu(1)=1\)
k有多个最小质因子,令\(y\)为k的最小质因子,\(z=\frac{k}{y}\)
- z没有多个因子,仅当枚举到\(d=y\)时,\(\mu(\frac{k}{d})=\mu(i)\)不为0,其余为0,\(f(x)=\mu(z)\)
- z有多个因子,都为0,\(z\)的情况等同于\(k\)的情况,为了方便统计还是令\(f(x)=\mu(z)\)
k只有一个最小因子
对于每一个\(\mu(\frac{k}{p})=\mu(\frac{z\times y}{p})\)
而\(z \text{ mod } y =0\)
根据\(\mu\)的定义有\(\mu(\frac{k}{p})=-\mu(\frac{z}{p})\),而且多了一项\(\mu(i)\)
所以线性筛出\(f\)的前缀和,然后数论分块就行了
约数个数和
首先有一个公式:
\[
\sum _{i=1}^{N}\sum_{j=1}^Md(ij)=\sum _{i=1}^{N}\sum_{j=1}^M\sum_{x | i} \sum_{y | j}[\operatorname{gcd}(x, y)=1]
\]
好像是有什么映射关系吧。。。避免统计重复
这里可以归纳成一个trick:枚举某个枚举的数的因子的时候可以将后面的sigma提前,枚举后面的数,前面的数的个数就可以直接计算出来了
然后枚举\(x\)和\(y\),设
\[
f(x)=\sum_{i=1}^{n} \sum_{j=1}^{m}\left\lfloor\frac{n}{i}\right\rfloor\left\lfloor\frac{m}{j}\right\rfloor[\operatorname{gcd}(i, j)=x]
\]
\[ g(x)=\sum_{i=1}^{n} \sum_{j=1}^{m}\left\lfloor\frac{n}{i}\right\rfloor\left\lfloor\frac{m}{j}\right\rfloor[\operatorname{x|gcd}(i, j)] \]
显然有:
\[
g(x)=\sum_{d=1}^{\left\lfloor\frac{n}{d}\right\rfloor}f(x\times d)
\]
然后有
\[
f(x)=\sum_{d=1}^{\left\lfloor\frac{n}{d}\right\rfloor}g(x\times d)\times \mu(d)
\]
普通的莫反题这里就结束了,因为g很容易求出
这题里的g怎么求呢?
变换一下:
\[
g(x)=\sum_{i=1}^{\frac{n}{x}} \sum_{j=1}^{\frac{m}{x}}\left\lfloor\frac{n}{i x}\right\rfloor\left\lfloor\frac{m}{j x}\right\rfloor
\]
\[ g(x)=\sum_{i=1}^{\frac{n}{x}} \left\lfloor\frac{n}{i x}\right\rfloor\sum_{j=1}^{\frac{m}{x}}\left\lfloor\frac{m}{j x}\right\rfloor \]
然后处理一下前缀和就可以\(O(1)\)求了
答案是\(f(1)\)
后记
其实还有好多题。。。
但是要杜教筛(感到弱小
之后补吧